Задача о размещении строящегося объекта

ВВЕДЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ

В методических указаниях рассматриваются задачи оптимизации для инженерных задач и решение их в среде MS Excel для строительных специальностей.

Интерес к этим задачам обусловлен спецификой их формализации и прикладной значимостью.

Функции MS Excel обладают развитым аппаратом численного анализа данных, позволяющим решать сложные задачи линейного и нелинейного программирования со многими неизвестными и ограничениями, что делает его очень удобным инструментом решения задач оптимизации.

В MS Excel для решения различных задач оптимизации есть средство Поиск решения. Эта команда находится в меню Сервис. Если команда не обнаруживается, это значит, надстройка Поиск решения не загружена. Для загрузки надо выбрать Надстройки из меню Сервис. Из списка диалогового окна выбирается Поиск решения и в квадратике устанавливается флажок. В случае отсутствия в списке надстройки Поиск решения, запускается программа установки MS Excel

Данные методические указания рассчитаны на читателей, знакомых с основами работы в Excel, и предназначены для студентов и слушателей курса информатики и информационных технологий в строительстве.

Методические указания содержат примеры решения задач оптимизации в среде MS Excel, а также задания для студентов строительных специальностей.

Часто возникает ситуация, когда необходимо выбрать из предложенных вариантов один, удовлетворяющий каким-то определенным требованиям. Очевидно, что этот вариант является оптимальным, т.е. наилучшим решением поставленной задачи. Введение нескольких характеристик (требований) для оценки наилучшего варианта приводит к задачам оптимизации.

Задачи оптимизации разделяются на классические и неклассические. В классических задачах требуется найти значения одной или нескольких переменных.. При этом ищется максимум или минимум значения некоторой непрерывной функции. В неклассических задачах имеются дополнительные ограничения, формирующие в совокупности множество допустимых альтернатив.

Задачи оптимизации на сегодняшний день разнообразны по своему характеру. Универсальных методов для их решения практически нет, но существуют типовые классы задач оптимизации, которые могут быть успешно решены с помощью программы электронных таблиц MS Excel. Некоторые из них рассмотрим в данных методических указаниях.

Задача о строительстве объекта относится к классу задач нелинейного программирования и является примером задачи многомернойнелинейной оптимизации.

В математической модели этой задачи используется две независимые переменные, каждая из которых представляет отдельную координату точки на плоскости.

 

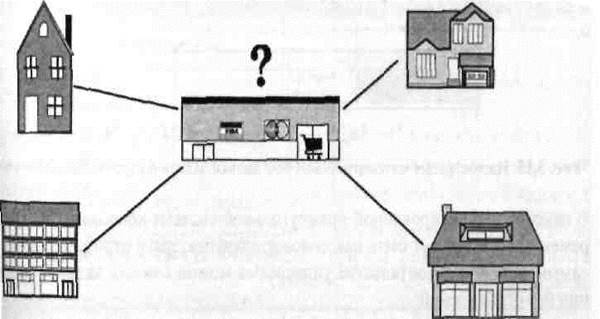
ЗАДАЧА О РАЗМЕЩЕНИИ СТРОЯЩЕГОСЯ ОБЪЕКТА

Задача может иметь несколько возможных вариантов постановки, отличающихся друг от друга количеством жилых домов и их расположением на координатной плоскости.

Рассмотрим конкретно один из вариантов этой задачи.

Имеются четыре жилых дома, расположенных в некотором микрорайоне города.

Определить местоположение объекта для строительства. Для примера объектом строительства выберем школу.

Требуется построить школу в удобном для всех жителей микрорайона месте, предполагая, что сумма расстояний от построенного объекта до всех жилых домов будет минимальным значением (рис. 1). Это значение и является целевой функцией, которое необходимо определить, используя функции среды MS Excel.

 

Рис. 1

Другие варианты задачи о строительстве объектов могут быть сформулированы как для различных значений количества домов, местоположения этих домов, так и для различных видов целевой функции.

ЗАДАЧА ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ

Задача об изготовлении стержней является разновидностью типовой задачи планирования производства и по своему характеру относится к классу задач геометрического программирования.

Задачи этого класса после предварительных преобразований могут быть эффективно решены с помощью модели целочисленного линейного программирования.

 

ЗАДАНИЕ 1 МЕСТОПОЛОЖЕНИЕ СТРОЯЩЕГОСЯ ОБЪЕКТА

По последней цифре номера зачетной книжки (студенческого билета) выбрать ваш номер варианта. По номеру варианта в табл. 1 выбрать соответственно количество домов микрорайона, координаты каждого дома и строящийся объект.

Таблица 1

№ варианта	Количество домов	Координаты домов	Строящийся объект
		(3,-4), (6,-8), (18,20)	почта
		(3,-6), (7,-10), (15,18), (26,-5)	универсам
		(4,-6), (8,-12), (16,11), (12,-24), (24,-48)	поликлиника
		(5,-5), (10,-10), (1,-20), (15,-15), (20,-7), (30,-2)	аптека
		(0,-5), (5,-10), (10,-20), (15,-15), (19,-7), (28,-2), (30, 10)	школа
		(-10,-5), (10,-1), (1,-20), (15,-15), (20,-17), (30,-2), (25,-30), (5,-10)	библиотека
		(5,-6), (10,-11), (1,-22), (15,-17), (20,-20), (30,-2), (0,1)	стадион
		(8,-5), (11,-14), (1,-25), (15,1), (20,-9), (30,-25)	школа
		(7,-5), (10,-10), (1,-20), (15,-15), (-4,10)	магазин
		(11,-5), (20,-10), (30,-20), (15,-15)	аптека

 

Замечание. Значения координат объектов могут быть, как положительными числами, так и отрицательными.

На листе разместить постановку задачи для целевой функции и данных. Для каждой целевой функции – нужен отдельный лист.

1. Создать на листе MS Excel макет задачи строящегося объекта, подписать ячейки с входными и выходными данными.

2. Внести нужные формулы в ячейки – создать компьютерную модель.

3. Показать в среде MS Excel графическое расположение домов микрорайона и строящегося объекта.

4. Выделить на графике имеющиеся дома и строящийся объект.

5. Получить решение задачи и сделать соответствующие выводы.

6. Выполнить решение на втором листе с другой функцией цели.

7. Продумать варианты выбора цели и возможные ограничения.

ЗАДАНИЕ 2 ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ ОПРЕДЕЛЕННЫХ РАЗМЕРОВ (РАСКРОЙ)ИЗ ЦЕЛЫХ ЗАГОТОВОК ПРОФИЛЯ

Задача состоит в том, чтобы из имеющихся исходных заготовок изготовить n комплектов требуемых длин стержней наиболее эффективным способом разрезания исходного материала, при котором на изготовление необходимого количества комплектов стержней потребуется наименьшее количество исходных заготовок.

1. По последней цифре номера зачетной книжки выбрать ваш номер варианта из табл. 2.

Таблица 2

 

№ варианта ри- ан- та	Количество способов разрезания заготовки	Количество комплектов деталей требуемой длины(шт.)	Заготовки	Нарезанные детали
Профиль (вид материала)	Длина исходных заготовок (м)	Требуемые длины (м)
			арматура	8,0	1,5	1,6	1,7
			доски	6,0	2,1	2,4	2,5
			трубы	7,0	1,4	1,9	0,8
			бревна	4,5	3,1	2,1	0,7
			уголок	12,4	2,4	2,6	2,45
			швеллер	8,4	1,8	1,5	2,1
			доски	6,4	2,4	1,5	0,9
			арматура	6,5	1,7	1,4	1,3
			трубы	5,5	2,1	2,7	3,2
			двутавр	7,2	1,9	2,1	2,4

 

 

2. Продумать способ раскроя.

3. Построить математическую модель в виде формул в ячейках листа. Внести примечания для формирования модели.

4. Заполнить ячейки вспомогательной таблицы 3, в которой представить способы разрезания, которые вам кажутся лучшими. Размер таблицы зависит от номера варианта. Количество столбцов этой таблицы соответствует указанному количеству способов разрезания заготовки. Остаток должен не превышать наименьшей требуемой длины.

Таблица 3

 

Способы разрезания
Длина 1
Длина 2
Длина 3
Длина 4
Длина n
Сумма отрезков
Остаток

 

5. Построить макет на листе MS Excel, при этом, подписывая все исходные данные, т.е. поясняя, в какой ячейке находится то или иное значение (использовать как подписи так и примечания.

6. Вписать в ячейки нужные формулы компьютерной модели для расчета суммы отрезков, подсчета остатка.

7. Составить формулу для целевой функции. Целевая функция – количество исходных (целых) заготовок, которые потребуется израсходовать.

8. Получить решение задачи (в целых числах исходных заготовок) и сделать соответствующие выводы.

Постановка задачи

Организация использует пять складов, на которых находится S1, S2, S3, S4, S5 тонн сырья. Его требуется доставить на 8 предприятий организации. Потребности предприятий в сырье равны P1, P2, P3, P4, P5, P6, P7, P8 соответственно, причем åSi = åPj. Стоимость перевозки 1 тонны сырья с i-го склада на j-е предприятие равна Aji (матрица {A} задана). Средствами поиска решения определить план перевозок, при котором фирма понесет наименьшие издержки по перевозкам, и определить эти издержки.

Номер варианта выбирается по сумме последних трех цифр зачетной книжки из таблицы

 

 

Варианты заданий

 

Рекомендации по математической модели и решению

Создать на листе математическую модель (см. ниже), задав в ней произвольные начальные значения (например, нули).

Вызвать средство поиска решения (меню Сервис) и установить параметры (рис. 4) и все требуемые ограничения (рис. 5).

рис. 4. Параметры поиска решения

 

рис. 5. Ограничения поиска решения

При выборе параметров рекомендуется использовать относительную погрешность 0,001 и допустимое отклонение 3-5%.

Изменяемые ячейки – план перевозок. Ограничения устанавливаются по смыслу задачи:

- весь товар должен быть вывезен со складов, и все предприятия должны полностью удовлетворить свою потребность;

- планируемые перевозки должны быть неотрицательны.

1. Найденное решение следует округлить до центнеров (1 знак после запятой) средствами форматирования ячеек.

рис. 6. Пример математической модели

 

рис. 7. Пример оформления решения задачи

 

Задача оптимизации плана выпуска продукции

Постановка задачи

Требуется составить план выпуска трех видов продукции П1, П2, П3. Для выпуска каждой единицы каждого вида продукции нужны ресурсы (сырье) четырех видов С1, С2, С3, С4 в количестве a_ij, где i – продукция, j – сырье. Запасы сырья C1, C2, C3, C4 – c1, c2, c3, c4 соответственно. Прибыль от выпуска единицы каждой продукции П1, П2, П3 – р1, р2, р3. Требуется максимизировать прибыль. При этом следует учесть ограничения:

Σa_ij·x_i≤c_j, j=1..4,

где x_i – количество произведенной продукции.

Варианты заданий

Номер варианта выбирается по сумме последних двух цифр зачетной книжки из таблицы

Варианты заданий приведены ниже в таблице

 

Рекомендации по математической модели и решению

1. Создать на листе математическую модель, задав в ней произвольные начальные значения (например, нули).

2. Вызвать средство поиска решения (меню Сервис) и установить параметры (рис. 8) и все требуемые ограничения (рис. 9).

рис. 8. Параметры поиска решения

 

рис. 9. Ограничения поиска решения

При выборе параметров рекомендуется использовать относительную погрешность 0,001 и допустимое отклонение 3-5%.

Изменяемые ячейки – Количество произведенной продукции. Ограничения устанавливаются по смыслу задачи:

- расходы сырья при производстве не должны быть больше запасов сырья;

- планируемые перевозки должны быть неотрицательны;

- количество производимой продукции должно быть целым.

рис. 10. Пример математической модели

 

 

ВВЕДЕНИЕ ЗАДАЧИ ОПТИМИЗАЦИИ

В методических указаниях рассматриваются задачи оптимизации для инженерных задач и решение их в среде MS Excel для строительных специальностей.

Интерес к этим задачам обусловлен спецификой их формализации и прикладной значимостью.

Функции MS Excel обладают развитым аппаратом численного анализа данных, позволяющим решать сложные задачи линейного и нелинейного программирования со многими неизвестными и ограничениями, что делает его очень удобным инструментом решения задач оптимизации.

В MS Excel для решения различных задач оптимизации есть средство Поиск решения. Эта команда находится в меню Сервис. Если команда не обнаруживается, это значит, надстройка Поиск решения не загружена. Для загрузки надо выбрать Надстройки из меню Сервис. Из списка диалогового окна выбирается Поиск решения и в квадратике устанавливается флажок. В случае отсутствия в списке надстройки Поиск решения, запускается программа установки MS Excel

Данные методические указания рассчитаны на читателей, знакомых с основами работы в Excel, и предназначены для студентов и слушателей курса информатики и информационных технологий в строительстве.

Методические указания содержат примеры решения задач оптимизации в среде MS Excel, а также задания для студентов строительных специальностей.

Часто возникает ситуация, когда необходимо выбрать из предложенных вариантов один, удовлетворяющий каким-то определенным требованиям. Очевидно, что этот вариант является оптимальным, т.е. наилучшим решением поставленной задачи. Введение нескольких характеристик (требований) для оценки наилучшего варианта приводит к задачам оптимизации.

Задачи оптимизации разделяются на классические и неклассические. В классических задачах требуется найти значения одной или нескольких переменных.. При этом ищется максимум или минимум значения некоторой непрерывной функции. В неклассических задачах имеются дополнительные ограничения, формирующие в совокупности множество допустимых альтернатив.

Задачи оптимизации на сегодняшний день разнообразны по своему характеру. Универсальных методов для их решения практически нет, но существуют типовые классы задач оптимизации, которые могут быть успешно решены с помощью программы электронных таблиц MS Excel. Некоторые из них рассмотрим в данных методических указаниях.

Задача о строительстве объекта относится к классу задач нелинейного программирования и является примером задачи многомернойнелинейной оптимизации.

В математической модели этой задачи используется две независимые переменные, каждая из которых представляет отдельную координату точки на плоскости.

 

ЗАДАЧА О РАЗМЕЩЕНИИ СТРОЯЩЕГОСЯ ОБЪЕКТА

Задача может иметь несколько возможных вариантов постановки, отличающихся друг от друга количеством жилых домов и их расположением на координатной плоскости.

Рассмотрим конкретно один из вариантов этой задачи.

Имеются четыре жилых дома, расположенных в некотором микрорайоне города.

Определить местоположение объекта для строительства. Для примера объектом строительства выберем школу.

Требуется построить школу в удобном для всех жителей микрорайона месте, предполагая, что сумма расстояний от построенного объекта до всех жилых домов будет минимальным значением (рис. 1). Это значение и является целевой функцией, которое необходимо определить, используя функции среды MS Excel.

 

Рис. 1

Другие варианты задачи о строительстве объектов могут быть сформулированы как для различных значений количества домов, местоположения этих домов, так и для различных видов целевой функции.