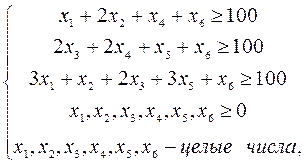Постановка задачи об изготовлении стержней

 

Способ изготовлений стержней заключается в разрезании исходной заготовки на отрезки заданной длины.

Задача состоит в том, чтобы из имеющихся исходных заготовок изготовить нужный комплект стержней требуемых длин наиболее эффективным способом разрезания исходного материала, при котором на изготовление необходимого количества комплектов стержней потребуется наименьшее количество исходных заготовок.

Аналогичные задачи встречаются часто на практике. В качестве исходных заготовок могут выбираться самые различные материалы, поступающие на строительство объектов в виде целых единиц, например, труб, досок, бревен, арматуры и т.д. При их использовании в строительстве приходится разрезать эти единицы заготовок на нужные отрезки. Длины этих отрезков должны соответствовать требуемым размерам.

При неправильном выборе разрезания заготовок теряется часть материала, остатки выбрасываются. Для более эффективного и экономичного способа разрезания предлагается применить математический метод оптимизации, причем он должен быть применен для всей партии заготовок. При использовании метода должны быть рассмотрены все возможные способы разрезания исходных заготовок. На этой основе попытаемся разработать математическую модель задачи об изготовлении стержней.

 

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ ОБ ИЗГОТОВЛЕНИИ СТЕРЖНЕЙ

Сущность задачи об изготовлении стержней заключается в следующем. Производственное предприятие изготавливает металлические стержни трех видов фиксированной длины: 2,9 м, 2,1 м и 1,5 м соответственно. Для изготовления этих стержней поступает партия заготовок исходного материала, которая также представляет собой металлические стержни длиной, например, 7,4 м. Способ изготовления стержней заключается в разрезании исходной заготовки на отрезки заданной длины. Длины отрезков выбираются самим производителем. Рассмотрим шесть способов разрезания указанных отрезков, например, как показано в таблице. В последней седьмой строке таблицы указаны остатки, полученные при разрезании стержня на отрезки требуемых длин, размеры длин указаны в 2, 3, 4 и 5 строках таблицы.

 

Таблица

 

Способы разрезания
Длина 1	2,9	2,9	2,1	2,9	2,1	2,9
Длина 2	1,5	2,9	2,1	2,1	1,5	2,1
Длина 3	1,5	1,5	1,5	2,1	1,5	1,5
Длина 4	1,5		1,5		1,5
Сумма отрезков	7,4	7,3	7,2	7,1	6,6	6,5
Остаток		0,1	0,2	0,3	0,8	0,9

 

Задача состоит в том, чтобы из имеющихся исходных заготовок изготовить 100 комплектов стержней требуемых длин наиболее эффективным способом разрезания исходного материала. При этом учесть, чтобы на изготовление необходимого количества комплектов стержней потребовалось наименьшее количество исходных заготовок.

Из стержня длиной 7,4 м можно, например, изготовить один комплект деталей, длины отрезков которых соответственно равны 2,9; 2,1; 1,5 м. Остаток после разрезания стержня будет равен 0,9 м.

Следовательно, если нужно получить 100 таких комплектов потребуется 100 стержней заготовок и оставшийся отход будет в сумме составлять 90 м.

В случае других предложенных методов, например первого способа разрезания остатков материала совсем не будет, но не будет и длины отрезка равной 2,1 м, а такой стержень необходим.

Исходная задача преобразуется в задачу определения оптимального числа различных способов разрезания исходных заготовок. При этом будет изготовлено заданное число стержней требуемой длины, а общее число исходных заготовок - минимальным.

Исходными переменными математической модели задачи об изготовлении стержней являются:

x_i – количество исходных заготовок, разрезанных i - ым способом для изготовления отдельных деталей.

Математическая постановка данной задачи может быть записана в виде:

,

 

где множество допустимых альтернатив формируется следующей системой ограничений типа неравенств:

 

 

 

(1)

 

т.к.из таблицы способов разрезания видно, что размер 2, 9 м для х₁ встречается один раз, для х₂ - два раза, для х₃ и х₅ не выбираются, х₄ и х₆ тоже один раз. Отрезков длиной 2,9 м выбирают не меньше 100 штук. Получаем первое неравенство системы. Точно также рассматриваем отрезки длиной 2,2 м и 1,5 м. Получаем следующие два неравенства. Значения не могут быть отрицательными числами, поэтому четвертое неравенство системы показывает, что каждое значение x_i больше или равно нулю. Предлагается коэффициенты при x_i первоначально выбрать равными единице и полагать x_i целыми.

Математическая модель (1) относится к классу задач целочисленного линейного программирования, которая может быть решена с помощь MS Excel.