
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристическое уравнение. Уравнение ЭйлераСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
В общем случае не существует алгоритма нахождения решения линейного однородного дифференциального уравнения n-го порядка
где Однако, если известно одно частное решение Пример. Рассмотрим
Тогда из уравнения следует, что
или Учитывая, что Второе решение фундаментальной системы решений уравнения - это В случае, когда
в виде
Уравнение Характеристическим уравнением линейного ДУ
Замечание. Пусть
Аналогично, можно проверить, что определитель Вронского Пример. Найти общее решение Решение. Если Из уравнения получим Замечание. Нетрудно видеть, что характеристическое уравнение Теорема (о кратных корнях). Пусть характеристическое уравнение (2) имеет корень
Доказательство. Для краткости изложения докажем утверждение для дифференциального уравнения второго порядка
характеристическое уравнение которого имеет вид Пусть
Тогда из уравнения (4) следует, что
или Учитывая, что
Отсюда в качестве второго решения мы можем взять Пример. Найти общее решение Решение. Характеристическое уравнение имеет вид: Алгебраическое уравнение имеет корень Пример. Найти общее решение Решение. Характеристическое уравнение имеет вид: Теорема (о комплексных корнях). Пусть характеристическое уравнение (2) имеет комплексные сопряженные корни
Доказательство. Для краткости изложения докажем утверждение для дифференциального уравнения второго порядка (4), характеристическое уравнение которого имеет вид
и
По теореме о линейном пространстве решений Пример. Найти общее решение Решение. Характеристическое уравнение имеет вид: Алгебраическое уравнение имеет комплексные сопряженные корни Пример. Найти общее решение Решение. Характеристическое уравнение имеет вид: Следствие. Общее решение уравнения а) б) в) Уравнение Эйлера
где Пример. Найти общее решение уравнения: Решение. Полагаем или Также как (1) решается уравнение вида
где Действительно, Пример. Найти общее решение уравнения: Решение. Полагаем Характеристическое уравнение Найти общее решение: 1. 5. 9. Задачи на самостоятельное решение: 2.1. Ответы: 2.1. 2.3. 2.4.
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 914; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.241 (0.006 с.) |

 ,
, , …,
, …,  , - непрерывные функции, но не постоянные.
, - непрерывные функции, но не постоянные. , то порядок уравнения можно понизить, выполнив замену переменной
, то порядок уравнения можно понизить, выполнив замену переменной  , при этом вновь получается линейное однородное дифференциальное уравнения, но уже
, при этом вновь получается линейное однородное дифференциальное уравнения, но уже  -го порядка с зависимой переменной
-го порядка с зависимой переменной 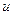 .
. . Пусть
. Пусть  .
.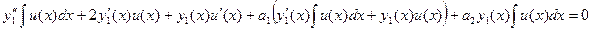
 .
. , окончательно получим линейное однородное дифференциальное уравнение первого порядка (уравнение с разделяющимися переменными)
, окончательно получим линейное однородное дифференциальное уравнение первого порядка (уравнение с разделяющимися переменными)  , решение которого
, решение которого  .
. .
. , …,
, …,  - постоянные, Эйлер предложил искать решение
- постоянные, Эйлер предложил искать решение (1)
(1) , где
, где 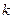 - постоянная. Подставляя
- постоянная. Подставляя  .
. имеет
имеет 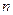 корней, с учетом кратности.
корней, с учетом кратности. называется алгебраическое уравнение
называется алгебраическое уравнение 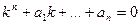 . (2)
. (2) - корни уравнения (2). Определитель Вронского
- корни уравнения (2). Определитель Вронского .
. , если (2) имеет
, если (2) имеет  различных корней
различных корней  ,
,  ,…,
,…,  для любого
для любого  . Следовательно,
. Следовательно,  ,
,  ,…,
,…,  - линейно независимые решения уравнения (1), которые можно включить в фундаментальную систему решений этого уравнения.
- линейно независимые решения уравнения (1), которые можно включить в фундаментальную систему решений этого уравнения. .
. .
. , т.е. характеристическое уравнение имеет вид
, т.е. характеристическое уравнение имеет вид  , корни которого
, корни которого  ,
,  . Следовательно, общее решение
. Следовательно, общее решение  .
.  на
на  ,
,  на
на  ,…,
,…,  на
на 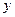 на
на  .
. . Тогда в фундаментальную систему решений уравнения (1) можно включить
. Тогда в фундаментальную систему решений уравнения (1) можно включить 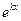 ,
,  ,
,  ,…,
,…,  . (3)
. (3) , (4)
, (4)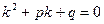 .
. ) этого характеристического уравнения и, следовательно,
) этого характеристического уравнения и, следовательно, 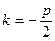 или
или  . Итак, одно решение (4)
. Итак, одно решение (4)  нам известно. Найдем второе решение фундаментальной системы решений (4), понизив порядок уравнения заменой
нам известно. Найдем второе решение фундаментальной системы решений (4), понизив порядок уравнения заменой 
 .
. , окончательно получим линейное однородное дифференциальное уравнение первого порядка (уравнение с разделяющимися переменными)
, окончательно получим линейное однородное дифференциальное уравнение первого порядка (уравнение с разделяющимися переменными)  , решение которого
, решение которого . Так как
. Так как .
.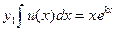 , поскольку
, поскольку  .
.  .
. .
. и корень кратности два
и корень кратности два  . Отсюда общее решение
. Отсюда общее решение  .
.  .
. . Данное алгебраическое уравнение имеет корень
. Данное алгебраическое уравнение имеет корень  (находится подстановкой). Делим
(находится подстановкой). Делим  на
на  и находим корни
и находим корни  уравнения
уравнения  . Следовательно,
. Следовательно,  . Отсюда общее решение
. Отсюда общее решение  .
.  кратности
кратности  решений:
решений: ,
,  ,…,
,…,  ,
,  ,
,  ,…,
,…,  . (5)
. (5) - корни характеристического уравнения. В этом случае кратность
- корни характеристического уравнения. В этом случае кратность  . Здесь
. Здесь 
 .
. и
и  являются также решениями (1), но, в отличие от
являются также решениями (1), но, в отличие от 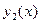 , - это вещественнозначные функции, которые и включают в фундаментальную систему решений.
, - это вещественнозначные функции, которые и включают в фундаментальную систему решений.  .
. .
.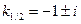 , т.е.
, т.е.  ,
,  Отсюда общее решение
Отсюда общее решение  .
. . Так как
. Так как  , то корни
, то корни 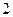 ,
,  .
.  . Отсюда общее решение:
. Отсюда общее решение:  .
.  имеет вид:
имеет вид: , если
, если  , если
, если  , т.е. характеристическое уравнение имеет единственный корень кратности два;
, т.е. характеристическое уравнение имеет единственный корень кратности два;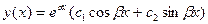 , если
, если  ,
,  (1)
(1) - постоянные при
- постоянные при  , заменой переменной
, заменой переменной  при
при  и
и  при
при  сводится к линейному дифференциальному уравнению с постоянными коэффициентами.
сводится к линейному дифференциальному уравнению с постоянными коэффициентами. при
при  . Отсюда
. Отсюда  ;
;  ;
;  . Следовательно,
. Следовательно, 
 . Характеристическое уравнение
. Характеристическое уравнение  и общее решение
и общее решение  .
. ,
, - постоянные,
- постоянные,  , заменой переменной
, заменой переменной  сводится к линейному дифференциальному уравнению с постоянными коэффициентами.
сводится к линейному дифференциальному уравнению с постоянными коэффициентами. . Отсюда
. Отсюда  ;
;  ;
;  и т.д.
и т.д. при
при  .
. . Отсюда
. Отсюда  . Отсюда
. Отсюда  ;
;  ;
;  . Следовательно, получим
. Следовательно, получим  .
. имеет корни
имеет корни 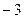 ,
,  .
. . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
. . 6.
. 6.  . 7.
. 7.  . 8.
. 8.  .
. . 10.
. 10.  . 11.
. 11.  . 12.
. 12.  .
. . 2.2.
. 2.2.  . 2.3.
. 2.3.  . 2.4.
. 2.4.  .
. . 2.2.
. 2.2.  .
. .
. .
.


