
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы ЛДУ. Алгебраический подходСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть дана система линейных однородных дифференциальных уравнений с постоянными коэффициентами:
Введем обозначения:
Тогда система (1) примет вид:
Теорема (о частном решении системы ДУ.). Пусть Доказательство. По предположению о том, что Замечание. Пусть матрица системы (1) имеет
Пример. Найти общее решение системы: Решение. Первый способ. Сведем систему к одному уравнению второго порядка:
Характеристическое уравнение имеет вид Второй способ. Сначала находим собственные значения матрицы
Общее решение системы:
Отсюда Ответ: Пример. Найти общее решение системы: Решение. Первый способ. Сведем систему к одному уравнению второго порядка:
Ответ: Второй способ. Сначала находим собственные значения матрицы
Частное решение
Пример. Найти общее решение системы: Решение. Сведем систему к одному уравнению второго порядка:
Характеристическое уравнение имеет вид Ответ. Разные задачи на уравнения второго порядка и системы: 1. 1. 1.3. 1.5.
1.8. 1.12. Задачи для самостоятельного решения: 2.1. 2.5. 2.8. 2.11. Ответы: 2.1.
2.4. 2.6. 2.12. 18.Устойчивость по Ляпунову. Основные понятия и определения Пусть задана нормальная система дифференциальных уравнений с начальными условиями в точке
Решение
для всех
Если же при сколь угодно малом Если решение
то это решение называется асимптотически устойчивым. Замечание. Если явление описывается системой ДУ с начальными условиями, которые являются результатами измерений и, следовательно, получены с некоторой погрешностью, то возникает вопрос о влиянии малого изменения начальных условий на искомое решение. Таблица 1.
Таблица 2.
Неустойчивое решение не имеет никакого прикладного значения. Рассмотрим двумерные автономные системы, т.е. системы вида
Если Простейшие типы точек покоя: Особая точка называется узлом, если каждая траектория примыкает к ней, имея определенную касательную. Особая точка называется центром, если она окружена только замкнутыми траекториями. Особая точка называется фокусом, если траектория асимптотически приближается к ней, навиваясь на нее в виде спиралей. Особая точка называется седлом, если две пары полутраекторий примыкают к ней, имея определенные касательные, а остальные кривые проходят в окрестности этой точки так, как должны идти горизонтали на карте местности, представляющей собой горный перевал.
Замечание. Исследование на устойчивость решения В дальнейшем, без ограничения общности. Можно считать, что на устойчивость исследуется тривиальное решение или, что одно и то же, расположенное в начале координат точка покоя системы ДУ.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.55.42 (0.007 с.) |

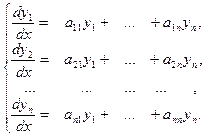 (1)
(1) ,
,  ,
,  .
.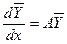 . (2)
. (2) - собственный вектор матрицы
- собственный вектор матрицы 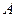 , принадлежащий собственному значению
, принадлежащий собственному значению  . Тогда
. Тогда  - решение системы (1).
- решение системы (1).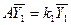 Так как
Так как  , то
, то 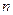 различных собственных значений
различных собственных значений 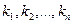 . Как известно из курса линейной алгебры, собственные векторы
. Как известно из курса линейной алгебры, собственные векторы  , принадлежащие различным собственным значениям, линейно независимы. Отсюда общее решение системы (1) имеет вид:
, принадлежащие различным собственным значениям, линейно независимы. Отсюда общее решение системы (1) имеет вид: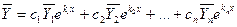

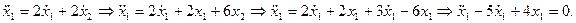
 . Отсюда два вещественных различных корня
. Отсюда два вещественных различных корня  ,
, 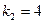 . Следовательно,
. Следовательно, 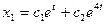 . Так как из первого уравнения
. Так как из первого уравнения  , то
, то 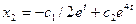 .
.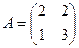 . Характеристическое уравнение имеет вид
. Характеристическое уравнение имеет вид 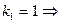
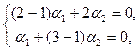
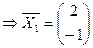 .
. 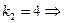
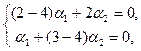
 .
. .
.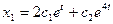 ,
, 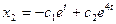 . Чтобы записать ответ так же как в предыдущем случае, полагаем
. Чтобы записать ответ так же как в предыдущем случае, полагаем 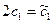 .
.
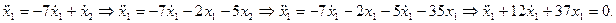 Характеристическое уравнение
Характеристическое уравнение 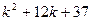 имеет два комплексно сопряженных корня
имеет два комплексно сопряженных корня 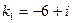 ,
, 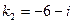 . Отсюда общее решение
. Отсюда общее решение 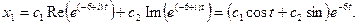 Так как из первого уравнения
Так как из первого уравнения  , то
, то 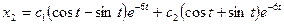
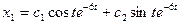 ,
, 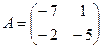 . Характеристическое уравнение имеет вид
. Характеристическое уравнение имеет вид 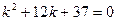 . Отсюда два комплексно сопряженных собственных значения
. Отсюда два комплексно сопряженных собственных значения 
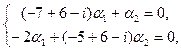
 .
. Общее решение системы:
Общее решение системы: Полагая
Полагая 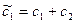 ,
, 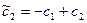 , получим тот же самый ответ:
, получим тот же самый ответ: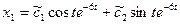 ,
,  .
.
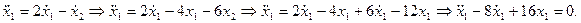
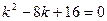 . Отсюда один вещественный корень кратности два
. Отсюда один вещественный корень кратности два  . Следовательно,
. Следовательно, 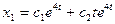 . Так как из первого уравнения
. Так как из первого уравнения 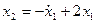 , то
, то  .
. ; 1.2.
; 1.2.  ;
; ; 1.4.
; 1.4. 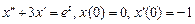 ; 1.6.
; 1.6.  . 1.7.
. 1.7. 
 1.9.
1.9. 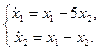 1.10.
1.10. 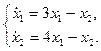 1.11.
1.11. 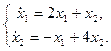
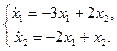 1.13.
1.13. 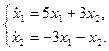 1.14.
1.14. 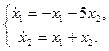 1.15.
1.15. 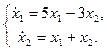 1.16.
1.16. 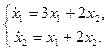 1.17.
1.17. 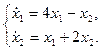 1.18.
1.18. 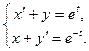
 2.2.
2.2. 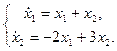 2.3.
2.3.  2.4.
2.4. 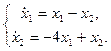
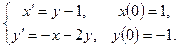 2.6.
2.6. 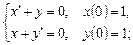 2.7.
2.7. 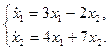
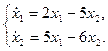 2.9.
2.9. 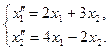 2.10.
2.10. 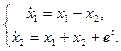
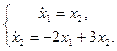 2.12.
2.12. 
 2.2.
2.2. 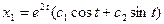 ;
;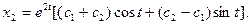 2.3.
2.3.  ;
; 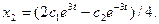
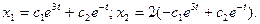 2.5.
2.5. 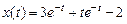 ,
, 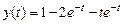 .
. ,
,  . 2.7.
. 2.7. 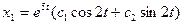 ;
; 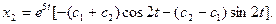 2.8.
2.8.  ;
;  2.9.
2.9. 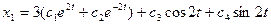 ;
;  . 2.10.
. 2.10.  ;
;  2.11.
2.11. 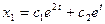 ,
,  ;
;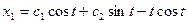 ,
, 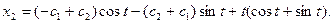
 :
: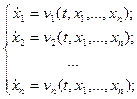 (1)
(1)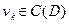 и
и  , т.е. непрерывны в области определения
, т.е. непрерывны в области определения 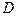 .
.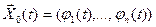 системы (1) называется устойчивым по Ляпунову, если для любого
системы (1) называется устойчивым по Ляпунову, если для любого  найдется такое
найдется такое  , что для всякого решения
, что для всякого решения 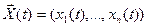 той же системы, значения которого в точке
той же системы, значения которого в точке 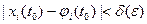 ,
,  , (2)
, (2)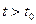 справедливы неравенства
справедливы неравенства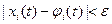 ,
, 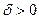 хотя бы для одного решения
хотя бы для одного решения 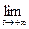
 ,
, 

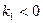 ,
,

 ,
,
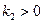

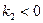


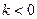

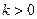

 (4)
(4)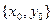 - точка покоя системы (4), т.е.
- точка покоя системы (4), т.е. 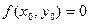 и
и  , то
, то 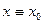 ,
, 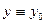 - это одно из решений системы. Такое решение изображается на фазовом портрете точкой.
- это одно из решений системы. Такое решение изображается на фазовом портрете точкой.


