
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция Ляпунова. Теорема Четаева о неустойчивостиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Теорема Четаева (о неустойчивости). Если существует дифференцируемая функция
б) В области Доказательство. Начальную точку
что противоречит ограниченности непрерывной функции Пример. Исследовать на устойчивость тривиальное решение Решение. Пусть функция Ляпунова Для проверки выполнения условия б) вычисляем
Отсюда Ответ: тривиальное решение Исследовать на устойчивость тривиальное решение 1. 5. Ответы: 1. 5.
Приложение 1 Таблица основных интегралов 1. 4. 7. 9. 11. 13. 15.
Приложение 2. Тест Не производя вычислений, необходимо выбрать правильный ответ или ответить на вопрос. 1. Какое из утверждений для числа особых решений уравнения 2. Какое из утверждений для порядка уравнения 3. Пусть
4. Выполняются ли предположения теоремы Коши для уравнения 5. Линейная комбинация решений дифференциального уравнения является решением уравнения: а) всегда; б) для линейного однородного уравнения с постоянными коэффициентами; в) для любого линейного однородного уравнения; г) для линейного неоднородного уравнения с постоянными коэффициентами; д) для любого линейного неоднородного уравнения? 6. Пусть определитель Вронского системы функций равен 0. Какое из утверждений для системы функций верно: а) линейно зависима; б) линейно независима; в) ничего нельзя сказать о линейной зависимости или линейной независимости системы функций? 7. Какие из систем функций линейно независимы: а) 8. Общее решение линейного неоднородного уравнения есть сумма … и …. Вставьте пропущенные слова из списка: а) частного решения однородного уравнения; б) общего решения однородного уравнения; в) частного решения неоднородного уравнения; г) общего решения неоднородного уравнения. 9. Определить типы дифференциальных уравнений: 1) 2) 5) 9. Определите типы дифференциальных уравнений: 1) а) Риккати; б) с разделяющимися переменными; в) однородное; г) Бернулли; д) Клеро. 10. Установите соответствие между уравнениями: 1) 2) Список литературы 1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов.- М.: Наука, Изд-во физ.- мат.литературы, 1986.-544 с. 2. Красносельский М.А. Векторные поля на плоскости// М.А. Красносельский, А.И. Перов, А.И. Поволоцкий, П.П. Забрейко.- М.: Изд-во физ.- мат.литературы, 1963.-248 с. 2. Кишенский С.Ж., Алексеевская Е.Д. Пособие к практическим занятиям по дисциплине “Дифференциальные уравнения” для студентов II курса специальности 01.02 дневного обучения.- М.: МГТУ ГА, 1999. 4. Любимов В.М., Козлова В.С. Обыкновенные дифференциальные уравнения: Пособие по изучению дисциплины и контрольные задания. - М.: МГТУ ГА, 2005. 5. Самохин А.В., Жулева Л.Д., Шевелева В.Н., Дементьев Ю.И. Сборник задач по высшей математике, часть VI, интегралы, дифференциальные уравнения для студентов I, II курса дневного отделения всех специальностей.- М.: МГТУ ГА, 2005. 6. Сборник задач по математике для втузов. В 4-х частях. Ч 3.: Учебное пособие для втузов // Под. ред. А.В. Ефимова, А.С.Поспелова. - М.: Изд-во физ.-мат.литературы, 2003. 7. Пантелеев А.В., Якимова А.С., Босов А.В. Обыкновенные дифференциальные уравнения в примерах и задачах: Учебное пособие.- М.: Высшая школа 2001.- 376 с. 8. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям.- Москва-Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2003.- 176 с. 9. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. - М.: Наука, Изд-во физ.- мат.литературы, 1969.- 424 с. 10. Эльсгольц Л.Э. Дифференциальные уравнения. Изд.7, М.: Едиториал УРСС, 2008.- 320 с.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 , называемая функцией Ляпунова, удовлетворяющая в некоторой замкнутой
, называемая функцией Ляпунова, удовлетворяющая в некоторой замкнутой  -окрестности начала координат условиям:
-окрестности начала координат условиям: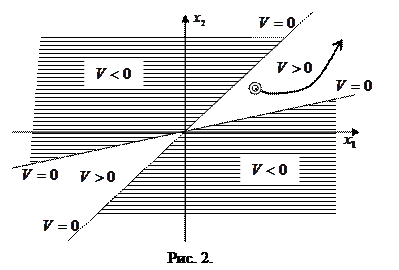 а)
а) 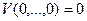 и в сколь угодно малой окрестности начала координат имеются точки, в которых
и в сколь угодно малой окрестности начала координат имеются точки, в которых  .
.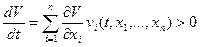 , причем в области
, причем в области  ,
,  , производная
, производная 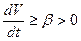 , то точка покоя
, то точка покоя 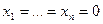 системы (1) неустойчива.
системы (1) неустойчива.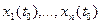 возьмем в сколь угодно малой окрестности начала координат в области
возьмем в сколь угодно малой окрестности начала координат в области 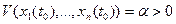 . Так как по условию б) производная
. Так как по условию б) производная 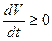 , то функция
, то функция 
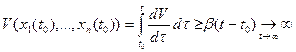 ,
,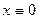 ,
,  системы
системы 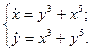
 . Тогда
. Тогда 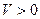 , если
, если 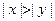 , т.е. условие а) теоремы Четаева выполнено.
, т.е. условие а) теоремы Четаева выполнено.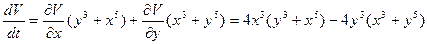 .
.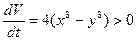 , если
, если 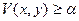 , для любого
, для любого  , что производная
, что производная 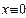 ,
,  2.
2.  3.
3. 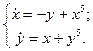 4.
4. 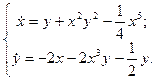

 . Неустойчива. 2.
. Неустойчива. 2.  . Асимптотически устойчива. 3.
. Асимптотически устойчива. 3.  . Асимптотически устойчива.
. Асимптотически устойчива.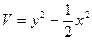 . Неустойчива.
. Неустойчива.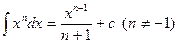 ; 2.
; 2.  ; 3.
; 3. 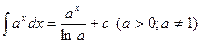 ;
;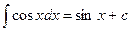 ; 5.
; 5. 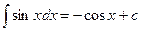 ; 6.
; 6. 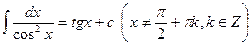 ;
;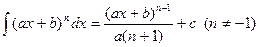 ; 8.
; 8. 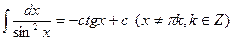 ;
;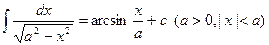 ; 10.
; 10. 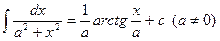 ;
;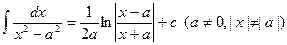 ; 12.
; 12. 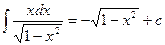 ;
;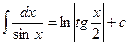 ; 14.
; 14. 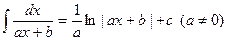 ;
; .
. верно: число особых решений уравнения равно а) двум; б) одному; в) нет особых решений?
верно: число особых решений уравнения равно а) двум; б) одному; в) нет особых решений?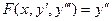 верно: порядок дифференциального уравнения равен а) двум; б) одному; в) трем?
верно: порядок дифференциального уравнения равен а) двум; б) одному; в) трем? - общий интеграл дифференциального уравнения,
- общий интеграл дифференциального уравнения,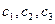 - константы. Какое из утверждений для порядка уравнения верно: порядок дифференциального уравнения равен а) двум; б) одному; в) трем?
- константы. Какое из утверждений для порядка уравнения верно: порядок дифференциального уравнения равен а) двум; б) одному; в) трем?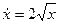 на интервале
на интервале 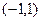 ?
?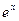 ,
,  ; б)
; б) 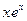 ; в)
; в) 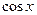 ,
, 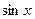 ?
?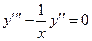 ;
;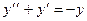 ; 3)
; 3) 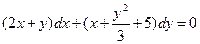 ; 4)
; 4)  ;
;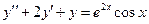 , выбрав нужный ответ из списка: а) уравнение, допускающее понижение порядка; б) уравнение в полных дифференциалах; в) линейное неоднородное уравнение порядка выше 1; г)уравнение Эйлера; д) линейное однородное уравнение порядка выше 1.
, выбрав нужный ответ из списка: а) уравнение, допускающее понижение порядка; б) уравнение в полных дифференциалах; в) линейное неоднородное уравнение порядка выше 1; г)уравнение Эйлера; д) линейное однородное уравнение порядка выше 1.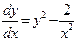 ; 2)
; 2) 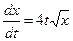 ; 3)
; 3)  ; 4)
; 4) 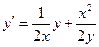 ; 5)
; 5)  , выбрав нужный ответ из списка:
, выбрав нужный ответ из списка: ;
;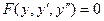 ; 3)
; 3) 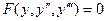 и заменами, с помощью которых они решаются: а)
и заменами, с помощью которых они решаются: а)  ; б)
; б) 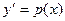 ; в)
; в)  .
.


