
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ДУ с разделяющимися переменнымиСодержание книги Поиск на нашем сайте
К дифференциальным уравнениям с разделяющимися переменными относятся пять видов дифференциальных уравнений: 1. Уравнение вида Пример. Найти решение задачи Коши Решение. Найдем сначала общее решение
Используя начальное условие
Ответ: 2. Уравнение вида Пример. Найти решение задачи Коши Решение. Найдем сначала общее решение
Используя начальное условие
Ответ: 3. Уравнение вида Интегрируется после “разделения переменных”, т.е. приведения путем умножения и деления к виду В одну часть входят только функции от 4. Уравнение вида Интегрируется также после “разделения переменных”, т.е. приведения путем умножения и деления к виду В одну часть входят только функции от Пример. Найти общий интеграл Решение. Разделяем переменные
Получили семейство окружностей. Ответ: 5. Иногда к уравнениям с разделяющимися переменными относят уравнение вида Пример. Найти общий интеграл Решение. Полагаем
Найти общий интеграл: 1. 1. 1.4. Задачи для самостоятельного решения: 2.1. 2.4. Ответы: 2.1. 2.4. 2.7. 2.10. Однородные ДУ. Уравнения, приводимые к однородным уравнениям
I. Функция Однородным дифференциальным уравнением называется уравнение вида
или Однородное уравнение приводится с помощью замены
к уравнению с разделяющимися переменными. Действительно, из (2) следует, что
Замечание. Если Пример. Найти общий интеграл Решение. Данное уравнение однородное, так как Находим общее решение, вычисляя интеграл в левой части методом неопределенных коэффициентов:
где II. Рассмотримуравнение
Пусть Пример. Найти общий интеграл уравнения Решение. Вычисляем Из уравнения получим
Далее решаем уравнение с разделяющимися переменными:
В результате
III. Пусть
Таким образом, будем иметь однородное уравнение, если
Пример. Найти общий интеграл уравнения Решение. Вычисляем Из уравнения получим
Таким образом, будем иметь однородное уравнение, если
Находим решение однородного уравнения:
Следовательно,
В результате
Решить уравнения: 1.1. 1. 5. 1.8. 1.10. Задачи для самостоятельного решения: 2.1. 2.4. 2.7. 2.10. 2.13. 2.15. 2.18. Ответы:2.1. 2.4.
ЛДУ. Уравнения Бернулли
Пусть
называется линейным дифференциальным уравнением (ЛДУ) первого порядка, а уравнение
где По методу Бернулли решение ищем в виде произведения двух неизвестных функций:
а из (2)
В обоих случаях получаем уравнения с разделяющимися переменными. Заметим, что при Пример. Решить уравнение Решение. Данное уравнение является линейным дифференциальным уравнением первого порядка. По методу Бернулли решение ищем в виде произведения двух неизвестных функций:
Поэтому Ответ: Пример. Решить уравнение Решение. Это уравнение Бернулли с
Ответ: Решить уравнения: 1. 1. 1.8. Задачи для самостоятельного решения: 2.1. 2.4. 2.7. Ответы: 2.1. 2.4. 2.7.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.168.61 (0.011 с.) |

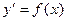 , не содержащее (явно) искомую функцию. Запишем его с помощью дифференциалов
, не содержащее (явно) искомую функцию. Запишем его с помощью дифференциалов 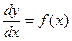 или
или 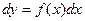 , откуда получим общее решение
, откуда получим общее решение 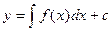 .
.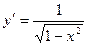 ,
, 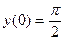 .
.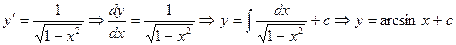 .
.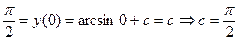 .
. .
.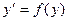 , не содержащее (явно) независимую переменную. Имеем
, не содержащее (явно) независимую переменную. Имеем  или
или  , откуда общий интеграл:
, откуда общий интеграл: 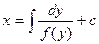 .
.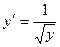 ,
, 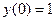 .
.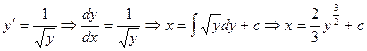 .
. .
.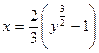 .
.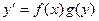 или
или  , в котором правая часть есть произведение функции, зависящей только от
, в котором правая часть есть произведение функции, зависящей только от 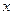 , на функцию, зависящую только от
, на функцию, зависящую только от 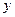 .
. .
. , а в другую – функция от
, а в другую – функция от 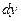 . Общий интеграл:
. Общий интеграл: 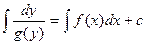 .
.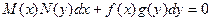 .
. .
.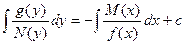 .
.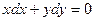 .
.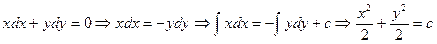 .
. .
.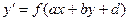 , где
, где  ,
, 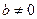 ,
, 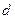 - постоянные. Заменой переменной
- постоянные. Заменой переменной 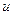 :
: 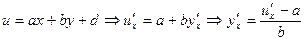 , получим уравнение
, получим уравнение  , т.е. уравнение вида 2.
, т.е. уравнение вида 2. .
.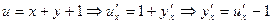 , получим уравнение
, получим уравнение  , т.е. уравнение вида 2. Отсюда
, т.е. уравнение вида 2. Отсюда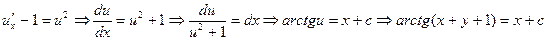 .
.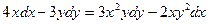 . 1.2.
. 1.2.  . 1.3.
. 1.3. 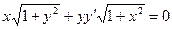 .
. . 1.5.
. 1.5.  . 1.6.
. 1.6. 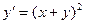 . 1.7.
. 1.7. 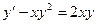 . 1.8.
. 1.8. 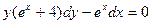 . 1.9.
. 1.9.  . 1.10.
. 1.10.  .
. . 2.2.
. 2.2. 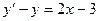 . 2.3.
. 2.3. 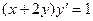 ,
, 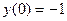 .
.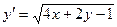 . 2.5.
. 2.5. 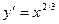 ,
,  . 2.6.
. 2.6. 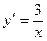 ,
, 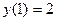 . 2.7.
. 2.7. 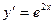 ,
, 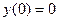 . 2.8.
. 2.8. 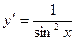 ,
, 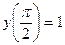 . 2.9.
. 2.9. 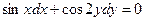 . 2.10.
. 2.10.  .
. . 2. 2.
. 2. 2. 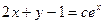 . 2.3.
. 2.3. 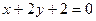 .
. . 2.5.
. 2.5. 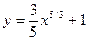 . 2.6.
. 2.6. 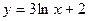 .
.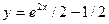 . 2.8.
. 2.8. 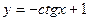 . 2.9.
. 2.9. 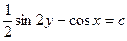 .
. .
.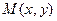 называется однородной функцией
называется однородной функцией 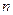 -го измерения, если для всех
-го измерения, если для всех 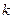 выполняется неравенство
выполняется неравенство 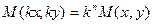 .
. (1)
(1)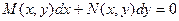 , где
, где 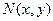 - однородные функции одного измерения.
- однородные функции одного измерения. (2)
(2)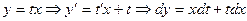 . Из (1) получаем
. Из (1) получаем 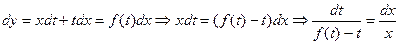 , т.е. уравнение с разделяющимися переменными, решение которого
, т.е. уравнение с разделяющимися переменными, решение которого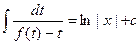 . (3)
. (3)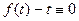 , то уравнение (1) имеет вид
, то уравнение (1) имеет вид  , т.е. изначально является уравнением с разделяющимися переменными. Если
, т.е. изначально является уравнением с разделяющимися переменными. Если 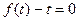 при значении
при значении  , то кроме решений, задаваемых формулой (3), существует также особое решение
, то кроме решений, задаваемых формулой (3), существует также особое решение 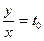 .
. .
.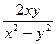 -однородная функция нулевого измерения. Полагаем
-однородная функция нулевого измерения. Полагаем  .
. ,
, 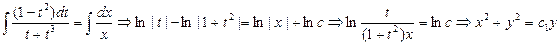 ,
, . Получили семейство окружностей, касающихся оси
. Получили семейство окружностей, касающихся оси  в начале координат. Кроме того, существует особое решение
в начале координат. Кроме того, существует особое решение 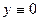 .
. 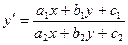 . (4)
. (4)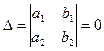 , тогда строки пропорциональны и
, тогда строки пропорциональны и 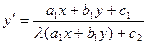 . Такое уравнение заменой
. Такое уравнение заменой 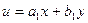 сводится к уравнению с разделяющимися переменными.
сводится к уравнению с разделяющимися переменными.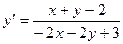 .
.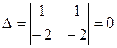 . Вводим новую зависимую переменную
. Вводим новую зависимую переменную 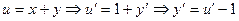 .
.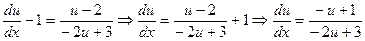 .
. .
.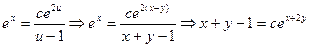 .
. 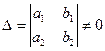 и, по крайней мере, одно из чисел
и, по крайней мере, одно из чисел  или
или  не равно нулю. Тогда уравнение (4) не является однородным, однако это уравнение можно привести к однородному путем введения новых переменных
не равно нулю. Тогда уравнение (4) не является однородным, однако это уравнение можно привести к однородному путем введения новых переменных 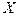 и
и 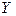 , где
, где 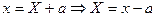 ,
,  . Подставляя в (4), получим
. Подставляя в (4), получим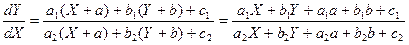 .
.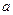 и
и 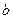 являются решением системы:
являются решением системы: .
.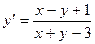 .
.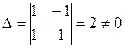 . Вводим новые переменные
. Вводим новые переменные 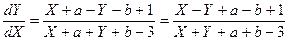 .
.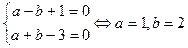 .
.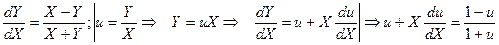 .
.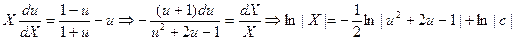 .
. .
.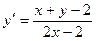 . 1.2.
. 1.2. 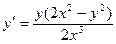 . 1.3.
. 1.3. 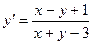 . 1.4.
. 1.4.  .
.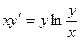 ,
,  . 1.6.
. 1.6.  . 1.7.
. 1.7.  .
. ,
, 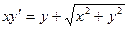 .
.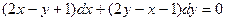 .
.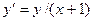 ; 2.2.
; 2.2.  ; 2.3.
; 2.3. 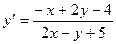 ;
; ; 2.5.
; 2.5.  ; 2.6.
; 2.6.  ;
; ; 2.8.
; 2.8. 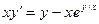 ; 2.9.
; 2.9. 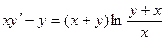 ;
;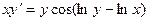 ; 2.11.
; 2.11. 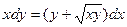 ; 2.12.
; 2.12. 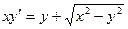 ;
;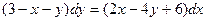 ; 2.14.
; 2.14. 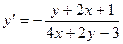 ;
;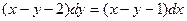 ; 2.16.
; 2.16. 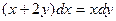 ; 2.17.
; 2.17.  ;
; ; 2.19.
; 2.19.  ; 2.20.
; 2.20.  .
.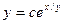 ; 2.2.
; 2.2. 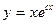 ; 2.3.
; 2.3. 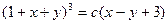 ;
;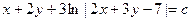 ; 2.5.
; 2.5.  ; 2.6.
; 2.6.  ; 2.7.
; 2.7. 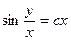 ; 2.8.
; 2.8. 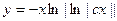 ; 2.9.
; 2.9. 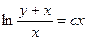 ; 2.10.
; 2.10. 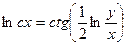 ; 2.11.
; 2.11.  ; 2.12.
; 2.12. 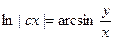 ; 2.13.
; 2.13. 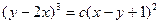 ; 2.14.
; 2.14. 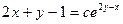 ; 2.15.
; 2.15. 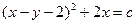 ; 2.16.
; 2.16. 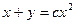 ; 2.17.
; 2.17. 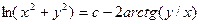 ; 2.18.
; 2.18. 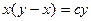 ; 2.19.
; 2.19. 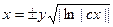 ; 2.20.
; 2.20. 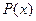 ,
, 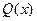 - непрерывные функции на заданном интервале
- непрерывные функции на заданном интервале 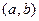 . Тогда уравнение
. Тогда уравнение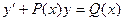 (1)
(1)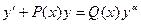 , (2)
, (2)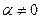 и
и 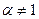 называется уравнением Бернулли.
называется уравнением Бернулли.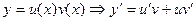 . Тогда из (1) следует
. Тогда из (1) следует
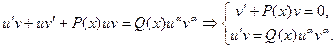
 уравнение Бернулли имеет решение
уравнение Бернулли имеет решение  .
.
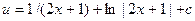 ,
, 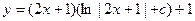 .
.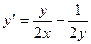 .
. . По методу Бернулли решение ищем в виде произведения двух неизвестных функций:
. По методу Бернулли решение ищем в виде произведения двух неизвестных функций: 
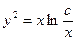 .
.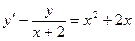 . 1.2.
. 1.2. 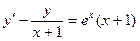 . 1.3.
. 1.3. 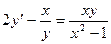 . 1.4.
. 1.4. 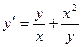 . 1.5.
. 1.5. 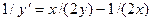 . 1.6.
. 1.6. 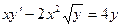 . 1.7.
. 1.7. 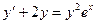 .
.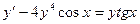 . 1.9.
. 1.9. 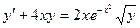 . 1.10.
. 1.10. 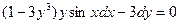 ,
,  .
. . 2.2.
. 2.2. 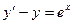 . 2.3.
. 2.3. 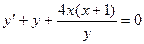 ,
, 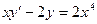 . 2.5.
. 2.5. 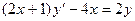 . 2.6.
. 2.6. 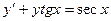 .
.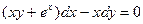 . 2.8.
. 2.8. 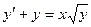 .
.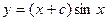 . 2.2.
. 2.2. 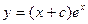 . 2.3.
. 2.3. 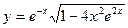 .
.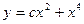 . 2.5.
. 2.5. 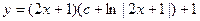 . 2.6.
. 2.6. 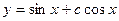 .
.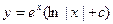 . 2.8.
. 2.8.  .
.


