
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения в полных дифференциалах. Интегрирующий множительСодержание книги
Поиск на нашем сайте
Уравнение вида
называется уравнением в полных дифференциалах, если левая часть является полным дифференциалом некоторой функции
Другими словами, левая часть (1) – это
В этом случае Действительно, Итак, чтобы решить уравнение (1), нужно восстановить функцию Пример. Решить уравнение Решение. Восстановим функцию
Итак, Ответ: В некоторых случаях условие (2) изначально может быть не выполнено, но можно подобрать функцию
т.е.
В развернутом виде (4) выглядит следующим образом:
Рассмотрим два частных случаях нахождения интегрирующего множителя. 1)
преобразуя которое получим
Если 2)
преобразуя которое получим
Если Пример. Найти общий интеграл Решение. Условие (2) не выполнено, так как
Подбираем функцию
т.е.
В развернутом виде последнее равенство выглядит следующим образом:
Полагая
Следовательно,
является уравнением в полных дифференциалах. Восстановим функцию
С другой стороны,
Ответ: Пример. Найти общий интеграл Решение. Условие (2) не выполнено, так как
Подбираем функцию
т.е.
В развернутом виде последнее равенство выглядит следующим образом:
Полагая
Интегрируя дважды по частям, находим
С другой стороны,
Ответ: Найти общий интеграл: 1. 3. 5. 7. 9.
8. Уравнения, не разрешенные относительно 1. Для решения уравнения вида Записываем дифференциал
Общее решение уравнения: Пример. Найти общее решение Решение. Вводим параметр
Записываем дифференциал
Ответ: Общее решение уравнения: 2. Решение уравнения вида
Записываем дифференциал
Ответ: Общее решение уравнения: Пример. Найти общее решение Решение. Вводим параметр Записываем дифференциал
Общее решение уравнения: 3. Уравнение вида Записываем дифференциал этой функции, учитывая, что
Если
решение которого При делении на Пример. Решить уравнение: Решение. Уравнение:
Записываем дифференциал этой функции, учитывая, что
Полагаем Выберем Следовательно,
При Ответ: Общее решение 4. Уравнение вида
Записываем дифференциал этой функции, учитывая, что
Полагая Заметим, что общее решение уравнения Клеро может быть получено формальной заменой Из равенства Пример. Решить уравнение Решение. Сначала преобразуем до вида уравнения Клеро
Записываем дифференциал этой функции, учитывая, что
Полагая Из равенства 5. Уравнение вида Пример. Найти общее решение Решение. Это уравнение Риккати с
Находим Следовательно, Поэтому общее решение Задачи: 1. Определите типы дифференциальных уравнений, выбрав нужный ответ из данного списка: а) уравнение, не разрешенное относительно производной, не содержащее явно зависимую переменную; б) уравнение, не разрешенное относительно производной, не содержащее явно независимую переменную; в) уравнение Клеро; г) уравнение Лагранжа; д) уравнение Риккати. 1.1. 1.5. 1.13. 2. Для совокупностей функций 2.1-2.8 определите тип уравнения из данного списка: а) уравнение, не разрешенное относительно производной, не содержащее явно зависимую переменную; б) уравнение, не разрешенное относительно производной, не содержащее явно независимую переменную; в) уравнение Клеро; г) уравнение Лагранжа, общим решением которого они являются. 2.1. 2. 3. Разные задачи на уравнения первого порядка: Найти общий интеграл: 3.1. 3.12. 3.17. Решить задачу Коши: 4. 1. 4. 3. 4. 5. 4. 7. 4. 9. 4. 11. 4. 13.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 571; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

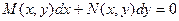 (1)
(1) , т.е.
, т.е. . (2)
. (2) , а (2) означает
, а (2) означает .
. является общим интегралом уравнения (1).
является общим интегралом уравнения (1). , при этом по теореме о неявной функции:
, при этом по теореме о неявной функции:  , откуда в силу равенств
, откуда в силу равенств  и
и  следует уравнение
следует уравнение  равносильное (1).
равносильное (1). .
. ,
,  . Следовательно, условие (2) выполнено, т.е. мы имеем уравнение в полных дифференциалах.
. Следовательно, условие (2) выполнено, т.е. мы имеем уравнение в полных дифференциалах. . С другой стороны,
. С другой стороны, .
. .
. .
. (интегрирующий множитель), при умножении на которую (1) получаем уравнение в полных дифференциалах:
(интегрирующий множитель), при умножении на которую (1) получаем уравнение в полных дифференциалах: , (3)
, (3) . (4)
. (4) . (5)
. (5) , т.е. интегрирующий множитель зависит только от
, т.е. интегрирующий множитель зависит только от 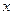 и (5) обращается в равенство
и (5) обращается в равенство ,
, или
или  .
. зависит только от
зависит только от  , т.е. интегрирующий множитель зависит только от
, т.е. интегрирующий множитель зависит только от 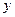 и (5) обращается в равенство
и (5) обращается в равенство ,
, или
или  .
. зависит только от
зависит только от  .
. .
. ,
, .
. .
. , получим
, получим .
. , откуда
, откуда  и
и
 .
. Итак,
Итак,  .
. .
. .
. .
. ,
, .
. .
. , получим
, получим  . Следовательно,
. Следовательно,  , откуда
, откуда  и
и  является уравнением в полных дифференциалах. Восстановим функцию
является уравнением в полных дифференциалах. Восстановим функцию  .
. .
.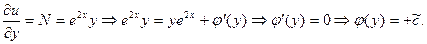 Итак,
Итак, .
. .
. . 2.
. 2.  .
. . 4.
. 4.  .
. . 6.
. 6.  .
. . 8.
. 8.  .
. . 10.
. 10.  .
. , Лагранжа, Клеро, Риккати
, Лагранжа, Клеро, Риккати , не разрешенного относительно
, не разрешенного относительно  :
:  .
. , учитывая, что
, учитывая, что  ,
, .
. ,
,  .
. .
. ) получаем
) получаем .
. .
. ,
,  .
. , не разрешенного относительно
, не разрешенного относительно  .
.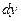 , учитывая, что
, учитывая, что  ,
,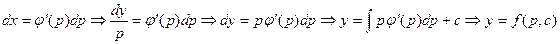 .
. ,
,  .
. .
. .
. .
. ,
,  .
.  , где
, где  и
и 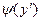 - заданные функции переменной
- заданные функции переменной  .
. .
. получим линейное уравнение первого порядка
получим линейное уравнение первого порядка ,
, вместе с
вместе с  дает общее решение.
дает общее решение. могут быть потеряны решения, соответствующие значениям параметра
могут быть потеряны решения, соответствующие значениям параметра  , при которых
, при которых  . Удовлетворяющие этому равенству значения параметра
. Удовлетворяющие этому равенству значения параметра  , получив, таким образом, функцию
, получив, таким образом, функцию  . Если эта функция является решением уравнения Лагранжа, то оно может быть частным решением, если входит в совокупность, определяющую общее решение, или особым, в противном случае.
. Если эта функция является решением уравнения Лагранжа, то оно может быть частным решением, если входит в совокупность, определяющую общее решение, или особым, в противном случае. .
. ,
, 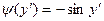 . Вводим параметр
. Вводим параметр  .
. или
или  получим линейное уравнение первого порядка
получим линейное уравнение первого порядка  .
. .
.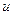 с условием, что
с условием, что  .
.
 из равенства
из равенства  получим решение
получим решение 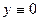 , являющееся особым решением.
, являющееся особым решением. ;
;  , где
, где  .
. .
. , получаем общее решение уравнения Клеро
, получаем общее решение уравнения Клеро  .
. .
. находим особое решение уравнения Клеро, задаваемое в параметрической форме,
находим особое решение уравнения Клеро, задаваемое в параметрической форме,  ,
,  .
. .
. . Вводя параметр
. Вводя параметр  .
. .
. , получаем общее решение уравнения Клеро
, получаем общее решение уравнения Клеро  .
. находим особое решение уравнения Клеро, задаваемое в параметрической форме,
находим особое решение уравнения Клеро, задаваемое в параметрической форме,  ,
,  или
или  . Исключая параметр
. Исключая параметр  .
. называется уравнением Риккати [1].В общем случае это дифференциальное уравнение неразрешимо в квадратурах. Если же известно одно частное решение
называется уравнением Риккати [1].В общем случае это дифференциальное уравнение неразрешимо в квадратурах. Если же известно одно частное решение  , то введением нового переменного
, то введением нового переменного  по формуле
по формуле  уравнение Риккати может быть сведено к линейному дифференциальному уравнению
уравнение Риккати может быть сведено к линейному дифференциальному уравнению 
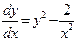 .
. ,
,  ,
,  . Заметим, что, если
. Заметим, что, если  , то
, то  . Поэтому
. Поэтому  . Получим
. Получим  и
и  или
или  , т.е.
, т.е.  . Полагаем
. Полагаем  . Отсюда
. Отсюда  . В итоге
. В итоге .
. из уравнения
из уравнения  , т.е.
, т.е.  и
и  .
. и
и  . Отсюда
. Отсюда  и
и  .
. .
.  . 1.2.
. 1.2.  . 1.3.
. 1.3.  . 1.4.
. 1.4.  .
. . 1.6.
. 1.6.  . 1.7.
. 1.7.  . 1.8.
. 1.8.  . 1.9.
. 1.9.  . 1.10.
. 1.10.  . 1.11.
. 1.11.  . 1.12.
. 1.12.  .
. . 1.14.
. 1.14.  .
. ,
,  . 2.2.
. 2.2.  .
. . 2.4.
. 2.4.  . 2 .5.
. 2 .5. 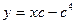 . 2 .6.
. 2 .6.  . 2.7.
. 2.7.  ;
;  . 2.8.
. 2.8.  ;
;  .
. . 3.2.
. 3.2.  . 3.3.
. 3.3.  . 3.4.
. 3.4.  . 3.5.
. 3.5.  . 3.6.
. 3.6.  . 3. 7.
. 3. 7.  . 3.8.
. 3.8.  . 3.9.
. 3.9.  . 3.10.
. 3.10.  . 3.11.
. 3.11. 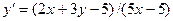 .
. . 3.13.
. 3.13.  . 3.14.
. 3.14.  . 3.15.
. 3.15.  . 3.16.
. 3.16.  .
. . 3.18.
. 3.18.  .
.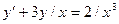 ,
,  . 4. 2.
. 4. 2.  ,
,  .
. ,
,  . 4. 4.
. 4. 4.  ,
,  .
. ,
,  . 4. 6.
. 4. 6.  ,
,  ,
, 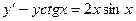 .
.  .
. ,
,  . 4. 10.
. 4. 10.  ,
,  .
. .
.  . 4. 12.
. 4. 12. 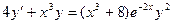 ,
,  .
.  . 4. 14.
. 4. 14.  ,
,  .
.


