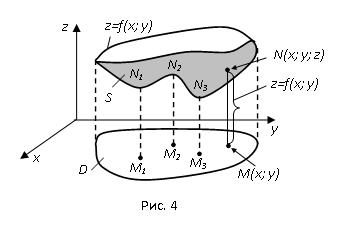
Определение частных производных функций нескольких переменных

Основные понятия функций нескольких переменных

Если каждой паре x и y значений двух независимых друг от друга переменных величин x и y из некоторой области их изменения t соответствует определенное значение z, то мы говорим, что z есть функция двух переменных x и y, определенная в области Д (z = f(x; y) – произвольная функция двух переменных: х и у – независимые переменные, z – функция от этих переменных).

Множество Д всех тех пар значений независимых переменных (x; y), для которых можно найти зависимую переменную (функцию) z, называется областью определения функции z = f(x; y).

Геометрически О.О. ф-ции изображается в виде некоторой совокупности точек на плоскости. Линию, ограничивающую данную область будем называть границей области. Точки, не лежащие на границе – внутренние точки области.

Область, состоящая из одних внутренних точек называется открытой или незамкнутой областью. Если же к области относятся точки границы, то область называется замкнутой.

Геометрическое место точек в системе координат, которое удовлетворяет уравнению z = f (x,y), называется графиком функции двух переменных.

7.2 Область определения функции нескольких переменных

Пусть z = f(x; y) – произвольная функция двух переменных: х и у – независимые переменные, z – функция от этих переменных. Множество D всех тех пар значений независимых переменных (x; y), для которых можно найти зависимую переменную (функцию) z, называется областью определения функции z = f(x; y). Так как каждая пара чисел (x; y) представляет собой некоторую точку плоскости хоу, то область определения D функции z = f(x; y) состоит из точек этой плоскости. Если функция z = f(x; y) определена для любых (x; y), то область D будет занимать всю плоскость хоу. А если не для любых - то какую-либо ее часть. И для каждой точки M(x; y) области D можно найти значение величины z = f(x; y) (одно или несколько). При этом переменные х и у на­зываются независимыми перемен­ными, или ар­гумен­тами, а перемен­ная z – зависимой перемен­ной, или функцией. Множество значений функции z на­зыва­ется областью изменения этой функ­ции. Если каждой паре чисел (х, у) из об­ласти определения функции соот­ветст­вует одно зна­чение – однозначной, в против­ном случае - многознач­ной. Графиком функции z=f(x, y) в пространстве XYZ является поверх­ность, представ­ляю­щая собой гео­метрическое место точек (х, у, f(х, у)), когда точка (х, у) про­бегает об­ласть определения функции. Эта поверхность может иметь вершины и впадины (N₁; N₂; N₃; …). Их проекции (M₁; M₂; M₃; …) на плоскость хоу (на область определения D) называются точками экстремума функции (точками ее максимума и минимума). Естественной областью опре­деле­ния ана­литически заданной функ­ции z=f (x, y)называ­ется сово­купность всех пар чисел (х, у), кото­рым соот­ветствуют действительные значения функции. Так, например, для функции z=ln(x²+y²-1) ес­тест­венная об­ласть определения состоит из всех пар чи­сел (х, у), для которых х²+у²-1>0, т. е. х²+у²>1.

Линии и поверхности уровня

Это еще один способ геометрической иллюст­рации функций двух переменных. Будем называть линией уровня функции z=f(x,y) геометрическое место точек (х, у) плоскости, в кото­рых функция принимает одно и то же значение С.

Линию уровня можно постро­ить, спроектировав на плоскость XOY множество точек пространства XYZ, лежащих в пересечении по­верхно­сти изображающей функцию z=f(x, y), и плоскости z=C.

Уравнение линии уровня имеет вид: f(x, y)=C. Изменяя С, мы будем получать различные линии уровня для данной функции.

Если положить С=С₁, С₂,…,Сп,…, выбрав эти числа в арифметиче­ской прогрессии с разностью h, то мы получим ряд линий уровня, по вза­имному рас­положению которых можно су­дить о характере изменения функции (рис. 7). В частности, там, где линии гуще, функция изменяется быстрее (поверхность, изображающая функцию, идет круче), а там, где линии уровня располагаются реже, функция изменяется медленнее (со­от­ветствующая поверхность будет более пологой). Кроме того, от­метки на линиях уровня дают непо­средственно значения функции в точках этих линий. Выбирая h дос­таточно малым, можно таким обра­зом получить до­вольно точное представление о поведении функ­ции.

Линии уровня часто используются при составлении географических, при составлении метеорологических карт.

Основные понятия функций нескольких переменных

Если каждой паре x и y значений двух независимых друг от друга переменных величин x и y из некоторой области их изменения t соответствует определенное значение z, то мы говорим, что z есть функция двух переменных x и y, определенная в области Д (z = f(x; y) – произвольная функция двух переменных: х и у – независимые переменные, z – функция от этих переменных).

Множество Д всех тех пар значений независимых переменных (x; y), для которых можно найти зависимую переменную (функцию) z, называется областью определения функции z = f(x; y).

Геометрически О.О. ф-ции изображается в виде некоторой совокупности точек на плоскости. Линию, ограничивающую данную область будем называть границей области. Точки, не лежащие на границе – внутренние точки области.

Область, состоящая из одних внутренних точек называется открытой или незамкнутой областью. Если же к области относятся точки границы, то область называется замкнутой.

Геометрическое место точек в системе координат, которое удовлетворяет уравнению z = f (x,y), называется графиком функции двух переменных.

7.2 Область определения функции нескольких переменных

Пусть z = f(x; y) – произвольная функция двух переменных: х и у – независимые переменные, z – функция от этих переменных. Множество D всех тех пар значений независимых переменных (x; y), для которых можно найти зависимую переменную (функцию) z, называется областью определения функции z = f(x; y). Так как каждая пара чисел (x; y) представляет собой некоторую точку плоскости хоу, то область определения D функции z = f(x; y) состоит из точек этой плоскости. Если функция z = f(x; y) определена для любых (x; y), то область D будет занимать всю плоскость хоу. А если не для любых - то какую-либо ее часть. И для каждой точки M(x; y) области D можно найти значение величины z = f(x; y) (одно или несколько). При этом переменные х и у на­зываются независимыми перемен­ными, или ар­гумен­тами, а перемен­ная z – зависимой перемен­ной, или функцией. Множество значений функции z на­зыва­ется областью изменения этой функ­ции. Если каждой паре чисел (х, у) из об­ласти определения функции соот­ветст­вует одно зна­чение – однозначной, в против­ном случае - многознач­ной. Графиком функции z=f(x, y) в пространстве XYZ является поверх­ность, представ­ляю­щая собой гео­метрическое место точек (х, у, f(х, у)), когда точка (х, у) про­бегает об­ласть определения функции. Эта поверхность может иметь вершины и впадины (N₁; N₂; N₃; …). Их проекции (M₁; M₂; M₃; …) на плоскость хоу (на область определения D) называются точками экстремума функции (точками ее максимума и минимума). Естественной областью опре­деле­ния ана­литически заданной функ­ции z=f (x, y)называ­ется сово­купность всех пар чисел (х, у), кото­рым соот­ветствуют действительные значения функции. Так, например, для функции z=ln(x²+y²-1) ес­тест­венная об­ласть определения состоит из всех пар чи­сел (х, у), для которых х²+у²-1>0, т. е. х²+у²>1.

Линии и поверхности уровня

Это еще один способ геометрической иллюст­рации функций двух переменных. Будем называть линией уровня функции z=f(x,y) геометрическое место точек (х, у) плоскости, в кото­рых функция принимает одно и то же значение С.

Линию уровня можно постро­ить, спроектировав на плоскость XOY множество точек пространства XYZ, лежащих в пересечении по­верхно­сти изображающей функцию z=f(x, y), и плоскости z=C.

Уравнение линии уровня имеет вид: f(x, y)=C. Изменяя С, мы будем получать различные линии уровня для данной функции.

Если положить С=С₁, С₂,…,Сп,…, выбрав эти числа в арифметиче­ской прогрессии с разностью h, то мы получим ряд линий уровня, по вза­имному рас­положению которых можно су­дить о характере изменения функции (рис. 7). В частности, там, где линии гуще, функция изменяется быстрее (поверхность, изображающая функцию, идет круче), а там, где линии уровня располагаются реже, функция изменяется медленнее (со­от­ветствующая поверхность будет более пологой). Кроме того, от­метки на линиях уровня дают непо­средственно значения функции в точках этих линий. Выбирая h дос­таточно малым, можно таким обра­зом получить до­вольно точное представление о поведении функ­ции.

Линии уровня часто используются при составлении географических, при составлении метеорологических карт.

Определение частных производных функций нескольких переменных

Пусть – некоторая функция двух переменных. Если зафиксировать одну из переменных (например, у), то функция станет функцией лишь одной переменной х. Если теперь найти производную функции z по этой оставшейся переменной х, то эта производная, имеющая несколько разных по форме обозначений

называется частной производной функции z по переменной х. Аналогично определяется, при фиксированном х и переменном у, частная производная функции z = f(x; y) по переменной y:

Познавательные статьи:



Формы дистанционного обучения

Передача мяча двумя руками снизу

Значение правильной осанки для жизнедеятельности человека

Основные ошибки при выполнении передач мяча на месте