
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения, не разрешенные относительно производной.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид При решении такого уравнения желательно разрешить его относительно
51. Системы дифференциальных уравнений. Основные определения. Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Не любое уравнение, содержащее производные неизвестной функции, является дифференциальным уравнением. Например, f¢(x) = f(f(x)) не является дифференциальным уравнением. Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него. Решением (интегралом) дифференциального уравнения порядка n называется функция y (x), имеющая на некотором интервале (a, b) производные Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Дифференциальное уравнение является линейным, если неизвестная функция и её производные входят в уравнение только в первой степени (и не перемножаются друг с другом). Общий вид:
Подклассом линейных уравнений являются однородные дифференциальные уравнения — уравнения, которые не содержат свободного члена: r (x) = 0. Для однородных дифференциальных уравнений выполняетсяпринцип суперпозиции: линейная комбинация частных решений такого уравнения также будет его решением. Все остальные линейные дифференциальные уравнения называются неоднородными дифференциальными уравнениями.
| 46 Дифференциальные уравнения n-го порядка. Дифференциальный оператор и его свойства.
Если старший коэффициент q 0 (x) отличен от нуля на интервале (a, b), т.е.
Задача Коши для уравнений и ставится также, как и для общего уравнения n -го порядка
где y 0, y 1, y 2, …, yn -1 - заданные числа. Для уравнения теорема существования и единственности решения задачи Коши требовала непрерывности функции
47 Однородные уравнения n-го порядка с постоянными коэффициентами. Теоремы об определителе Вронского. Уравнение n-го порядка для одной неизвестной функции z независимого переменного t с постоянными коэффициентами имеет вид: где a1,..,an - постоянные числа (действительные или комплексные). К уравнению (2.1), очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось. Решения уравнения (2.1) будут построены в явном виде и тем самым установлена еще раз теорема существования. Теорема единственности будет использоваться по существу для доказательства того, что найдены все решения данного уравнения. Определителем Вронского (вронскианом) системы n - 1 раз дифференцируемых функций y 1(x), y 2(x), …, yn (x) называется определитель
Теорема о вронскиане линейно зависимой системы функций. Если система функций y 1(x), y 2(x), …, yn (x) линейно зависима на интервале (a, b),то вронскиан этой системы тождественно равен нулю на этом интервале. Док-во. Если функции y 1(x), y 2(x), …, yn (x) линейно зависимы на интервале (a, b), то найдутся числа
Продифференцируем по x равенство(27) n -1 раз и составим систему уравнений:
Будем рассматривать эту систему как однородную линейную систему алгебраических уравнений относительно Итак, W (x) = 0 при
48 Характеристическое уравнение и фундаментальная система решения для различных его корней. Уравнение называется характеристическим уравнением, а его корни – характеристическими числами уравнения Система функций может выполняться только когда все
Еслифундаментальная система решений найдена, то функция дает общее решение однородного уравнения,(все
49 Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Основные определения. где Всякую функцию вид называют квазимногочленом. каждое решение линейного однородного уравнения с постоянными коэффициентами является квазимногочленом. Линейная комбинация квазимногочленов есть квазимногочлен; произведение двух квазимногочленов представляет собой квазимногочлен; если к произвольному квазимногочлену применить произвольный оператор L(p), то мы вновь получим квази многочлен.
50 Типы правых частей неоднородных дифференциальных уравнений n-го порядка с постоянными коэффициентами, их решение.
|
52. Метод исключения решений системы дифференциальных уравнений.
Системы дифференциальных уравнений n –го порядка можно решать сведением к уравнению n –го порядка. Такой метод решения систем называется методом исключения.
Рассмотрим, например, нормальную систему дифференциальных уравнений 2 –го порядка
 Исключим функцию y 2. Для этого сначала выразим y 2 через x и y 1 из первого уравнения системы, затем продифференцируем по x первое уравнение системы, заменяя y 2 полученным для него выражением, а производную y 2 − правой частью второго уравнения системы:
Исключим функцию y 2. Для этого сначала выразим y 2 через x и y 1 из первого уравнения системы, затем продифференцируем по x первое уравнение системы, заменяя y 2 полученным для него выражением, а производную y 2 − правой частью второго уравнения системы:
 Получили обыкновенное дифференциальное уравнение 2 –го порядка
Получили обыкновенное дифференциальное уравнение 2 –го порядка
 Таким же образом решают методом исключения произвольные системы n –го порядка: дифференцируют уравнения системы и, последовательно исключая функции y 2,..., yn и их производные, сводят систему к одному дифференциальному уравнению n –го порядка относительно y 1.
53. Метод Эйлера решения системы дифференциальных уравнений.
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенны дифференциальных уравнений.
Ломаная Эйлера (красная линия) — приближённое решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)
Пусть дана задача Коши для уравнения первого порядка
Таким же образом решают методом исключения произвольные системы n –го порядка: дифференцируют уравнения системы и, последовательно исключая функции y 2,..., yn и их производные, сводят систему к одному дифференциальному уравнению n –го порядка относительно y 1.
53. Метод Эйлера решения системы дифференциальных уравнений.
Метод Эйлера — наиболее простой численный метод решения (систем) обыкновенны дифференциальных уравнений.
Ломаная Эйлера (красная линия) — приближённое решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)
Пусть дана задача Коши для уравнения первого порядка
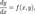

 где функция f определена на некоторой области где функция f определена на некоторой области 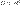 . Решение разыскивается на интервале . Решение разыскивается на интервале  . На этом интервале введем узлы . На этом интервале введем узлы
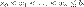 Приближенное решение в узлах Xi, которое обозначим через Yi определяется по формуле
Приближенное решение в узлах Xi, которое обозначим через Yi определяется по формуле
 Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
54. Метод суперпозиций решений системы дифференциальных уравнений.
Принцип суперпозиции: Если y 1(x) и y 2(x) — решения неоднородных линейных уравнений L (y) = f 1(x) и L (y) = f 2(x), то их сумма y (x) = y 1(x) + y 2(x) является решением уравнения L (y) = f 1(x) + f 2(x).
57. Признак Даламбера сходимости ряда.
Если для числового ряда
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
54. Метод суперпозиций решений системы дифференциальных уравнений.
Принцип суперпозиции: Если y 1(x) и y 2(x) — решения неоднородных линейных уравнений L (y) = f 1(x) и L (y) = f 2(x), то их сумма y (x) = y 1(x) + y 2(x) является решением уравнения L (y) = f 1(x) + f 2(x).
57. Признак Даламбера сходимости ряда.
Если для числового ряда  существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство существует такое число q, 0 < q < 1, что начиная с некоторого номера выполняется неравенство  то данный ряд абсолютно сходится; если же, начиная с некоторого номера то данный ряд абсолютно сходится; если же, начиная с некоторого номера  то ряд расходится.
Доказательство:
1. то ряд расходится.
Доказательство:
1.  , тогда существует , тогда существует  , существует , существует  , для любого , для любого  . Ряд из . Ряд из  сходится (как геометрическая прогрессия). Значит, ряд из сходится (как геометрическая прогрессия). Значит, ряд из  сходится (по признаку сравнения).
2. сходится (по признаку сравнения).
2.  , тогда существует , тогда существует  . .  для любого для любого  . Тогда . Тогда  не стремится к нулю и ряд расходится.
58. Радикальный признак Коши сходимости ряда.
Если для числового ряда не стремится к нулю и ряд расходится.
58. Радикальный признак Коши сходимости ряда.
Если для числового ряда  с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство с неотрицательными членами существует такое число d, 0 < d < 1, что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится.
Условие радикального признака равносильно следующему: , то данный ряд сходится.
Условие радикального признака равносильно следующему:
 То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 599; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.186.233 (0.012 с.) |

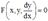
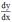 , т.е. получить одно или несколько уравнений, разрешенных относительно производной:
, т.е. получить одно или несколько уравнений, разрешенных относительно производной:  ,каждое из которых нужно решать. Не всегда уравнение (1) разрешается относительно
,каждое из которых нужно решать. Не всегда уравнение (1) разрешается относительно 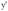 и еще реже полученные после разрешения уравнение легко интегрируется. Поэтому уравнение вида (1) часто приходится решать методом введения параметра. Более полно этот метод изложен в [3].Пусть уравнение (1) легко разрешается относительно y или относительно x, например, его можно записать в виде
и еще реже полученные после разрешения уравнение легко интегрируется. Поэтому уравнение вида (1) часто приходится решать методом введения параметра. Более полно этот метод изложен в [3].Пусть уравнение (1) легко разрешается относительно y или относительно x, например, его можно записать в виде  . Введя параметр
. Введя параметр  , получим
, получим  .Взяв полный дифференциал от правой и левой частей последнего равенства, и заменив dy через pdx, получим уравнение
.Взяв полный дифференциал от правой и левой частей последнего равенства, и заменив dy через pdx, получим уравнение  ,т.е.
,т.е.  .Если найдено решения этого уравнения
.Если найдено решения этого уравнения  , то решения исходного уравнения запишем в параметрическом виде
, то решения исходного уравнения запишем в параметрическом виде  .Примерами уравнений, которые решаются изложенным выше методом, являются уравнения Лагранжа
.Примерами уравнений, которые решаются изложенным выше методом, являются уравнения Лагранжа 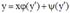 и Клеро
и Клеро  .
. до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести кквадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
до порядка n включительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести кквадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет.
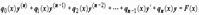 ;
;
 для
для  , то, умножая на
, то, умножая на  , приводим уравнение к виду со старшим коэффициентом, равным 1:
, приводим уравнение к виду со старшим коэффициентом, равным 1: ;
;
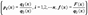 ; дальше мы будем рассматривать уравнение. Eсли правая часть уравнения тождественно равна нулю на рассматриваемом интервале (f (x)=0 при
; дальше мы будем рассматривать уравнение. Eсли правая часть уравнения тождественно равна нулю на рассматриваемом интервале (f (x)=0 при  ;
;
 : требуется найти решение уравнения или, удовлетворяющее начальным условиям
: требуется найти решение уравнения или, удовлетворяющее начальным условиям
 и её производных
и её производных  ; если привести к виду:
; если привести к виду:  ,
, 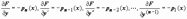 . Таким образом, условия теоремы Коши приводят к необходимости непрерывности функций f (x) и pi (x), i = 1, 2, …, n. Далее, вывод теоремы Коши для уравнения (17) заключался в том, что найдётся окрестность точки x 0, в которой существует однозначно определённое решение задачи Коши; для линейных уравнений (20) и (21) вывод более глобален: единственное решение существует на всём интервале (a, b), на котором выполняются условия теоремы:
. Таким образом, условия теоремы Коши приводят к необходимости непрерывности функций f (x) и pi (x), i = 1, 2, …, n. Далее, вывод теоремы Коши для уравнения (17) заключался в том, что найдётся окрестность точки x 0, в которой существует однозначно определённое решение задачи Коши; для линейных уравнений (20) и (21) вывод более глобален: единственное решение существует на всём интервале (a, b), на котором выполняются условия теоремы: 
 (2.1)
(2.1)
 , из которых хотя бы одно отлично от нуля, такие что
, из которых хотя бы одно отлично от нуля, такие что (27) для
(27) для 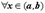

 . Определитель этой системы - определитель Вронского. При
. Определитель этой системы - определитель Вронского. При  эта система имеет нетривиальное решение
эта система имеет нетривиальное решение  , следовательно, в каждой точке её определитель равен нулю.
, следовательно, в каждой точке её определитель равен нулю. , т.е.
, т.е.  на (a, b).
на (a, b).
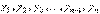 называетсялинейно независимой в интервале
называетсялинейно независимой в интервале  , если тождество (
, если тождество (  - постоянные числа)
- постоянные числа)
 . Если к тому же каждая из функций
. Если к тому же каждая из функций  является частным решением однородного уравнения,то система решений одно-родного уравнения называется фундаментальной системой решений.
является частным решением однородного уравнения,то система решений одно-родного уравнения называется фундаментальной системой решений.
 - константы).
- константы).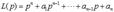 - дифференциальный оператор n-го порядка с постоянными коэффициентами, а F = F(t) - известная функция вида:
- дифференциальный оператор n-го порядка с постоянными коэффициентами, а F = F(t) - известная функция вида: 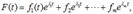 е1,е,еm - некоторые комплексные числа, a f1(t),??fm(t) - многочлены от t.
е1,е,еm - некоторые комплексные числа, a f1(t),??fm(t) - многочлены от t.

 , то
если
, то
если  ряд сходится,
если
ряд сходится,
если 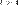 ряд расходится,
если
ряд расходится,
если  вопрос о сходимости ряда остается открытым.
вопрос о сходимости ряда остается открытым.



