
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2.2 Относительные величиныСодержание книги
Поиск на нашем сайте
Студент должен:
знать: - сущность относительных показателей;
- формы их выражения
- взаимосвязи абсолютных и относительных показателей;
уметь:
- рассчитывать различные виды относительных показателей;
- анализировать относительные показатели.
Относительные величины – это производные обобщающие показатели, выражающие качественную оценку экономических явлений в результате сравнения статистических данных. В числителе – сравниваемый показатель, в знаменателе – база сравнения.
Формы выражения относительных величин: коэффициенты, проценты, промилле, децимилле.
Виды относительных величин: 1. ОПСт – относительный показатель структуры
Расчёт: каждая часть совокупности делится на всю совокупность.
ОПСт = где ΣY
Форма выражения – проценты.
2. ОПСр – относительный показатель сравнения Расчёт: сравниваемый показатель одного объекта (экономически, социально более значимый или самая большая величина) делится на одноименные показатели каждого из объектов. ОПСр =
где Υ03 = Const
Формы выражения – коэффициенты или проценты.
3. ОПК – относительный показатель координации Расчёт: каждая часть совокупности делится на выбранную часть совокупности (принцип выбора, как в ОПСР).
ОПК =
где Υ2 = Const Это именованные величины.
В числителе и знаменателе – одинаковые наименования величин.
4. ОПИ – относительный показатель интенсивности Расчёт:
Показатель явления делится на показатель среды распространения этого явления.
ОПИ =
Это именованные величины.
В числителе и знаменателе - разные наименования величин.
ОПуэр – относительный показатель уровня экономического развития Расчёт: исследуемый макроэкономический показатель делится на численность населения страны.
ОПуэр = В числителе и знаменателе – разные наименования величин. 6. ОПДб – относительный показатель динамики базисный, т.е. с постоянной базой сравнения Расчёт: показатель текущего уровня делится на показатель базисного уровня (первый показатель по времени, если отсутствуют указания).
ОПДб = где Y0=Const
Формы выражения – проценты или коэффициенты.
7. ОПДц – относительный показатель динамики цепной, т.е. с переменной базой.
Расчет: показатель последующего уровня делится на показатель предыдущего уровня.
ОПДц = Формы выражения – проценты или коэффициенты.
8. ОПП – относительный показатель плана
Расчёт: уровень плана на последующий период делится на уровень текущего периода.
ОПП = Формы выражения – проценты или коэффициенты.
9. ОПРП – относительный показатель реализации плана Расчёт: уровень, достигнутый в последующем периоде, делится на уровень плана последующего периода.
ОПРП =
Формы выражения – проценты или коэффициенты.
ОПВДО – относительный показатель выполнения договорных обязательств Расчёт: фактический уровень делится на уровень по договору.
ОПВДО = Формы выражения – проценты или коэффициент Вопросы для самоконтроля 1. Что показывает относительный показатель структуры?
2. При каких условиях относительные показатели выражаются в коэффициентах, процентах, промилле, децемилле?
3. По каким принципам отбирается постоянная величина при расчёте относительных показателей сравнения и координации?
4. В чём сходство и различие относительных показателей сравнения и координации?
5. В чём сходство и различие относительных показателей координации и интенсивности?
6. В чём сходство и различие относительных показателей сравнения и динамики?
7. В чём сходство и различие относительных показателей динамики в базисной и цепной формах?
8. В чём сходство и различие относительных показателей плана и реализации плана?
9. В чём сходство и различие относительных показателей плана и договорных обязательств?
10. Приведете примеры показателей числителя при расчёте относительного показателя уровня экономического развития.
Тема 2.3. Средние величины Студент должен:
знать:
- сущность средних величин, единицы их измерения;
- виды средних величин;
- методы расчёта средних показателей;
уметь:
- рассчитывать средний уровень изучаемого явления.
Средние величины абстрактны, представляют собой обобщающие
показатели, рассчитываются на основе массовых данных, измеряются в той же размерности, что и признак. Приняты следующие обозначения:
х1, х2, х3, ….. хn (хi) – варианты, или индивидуальные значения признака;
f – частота признака;
Σ – знак суммирования;
n – количество единичных признаков;
i – порядковый номер;
Wi – произведение вариантов на частоту
ω - частости - % к итогу.
Виды средних величин:
1. Простая средняя арифметическая (невзвешенная) – это количество суммарного признака, делённое на число показаний:
Применяется для единичных значений признаков.
2. Взвешенная средняя арифметическая имеет в числителе сумму произведений варианта на частоту, а в знаменателе – сумму частот:
Применяется, когда значение признака повторяется несколько раз.
В интервальном ряду распределения определяется серединное значение В закрытом интервале серединное значение определяется как полусумма значений нижней и верхней границ. В открытом интервале предполагается, что расстояние между границами интервала такое же, как в соседнем интервале.
Тогда окончательная формула: 3. Простая средняя гармоническая – это величина, обратная средней арифметической.
Применяется, когда произведения по каждому признаку равны.
4. Взвешенная средняя гармоническая:
Применяется, когда даны произведения вариантов на частоту, а частота отсутствует.
Средняя геометрическая Применяется для отношения двух чисел, а также в рядах распределения в виде геометрической прогрессии.
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.186.62 (0.009 с.) |


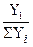 ;
; 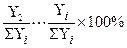
 = Const
= Const
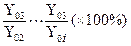


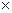 кратное число,
кратное число, кратное число.
кратное число.



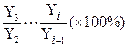



 - средняя величина признака;
- средняя величина признака; -серединное значение признака;
-серединное значение признака;

 =
= 





