Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения, приводящиеся к однородным.Стр 1 из 2Следующая ⇒
Уравнением, приводящимся к однородному, называется дифференциальное уравнение вида
Заменой u = y – y0, v = x – x0 это уравнение приводится к однородному уравнению
Здесь x0 и y0 — единственное решение линейной системы
| ||
31. Основные определения теории поля.
Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке M этой области соответствует определенное число U=U(M), говорят, что в области определено скалярное поле. Если в каждой точке M области пространства соответствует вектор  , то говорят, что задано векторное поое.
Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке.
Функции скалярного поля:
 .
32. Производная по направлению. Градиент.
Возьмем в пространстве, где задано поле U=U(x, y, z), некоторую точку M и найдем скорость изменения функции U при движении точки M в произвольном направлении λ. Пусть вектор λ имеет начало в точке M и направляющие его косинусы.
Приращение функции U, возникающее при переходе от точки M к некоторой точке M1 в направлении вектора λ определяется как 
Или  .
Тогда 
Производной от функции U=U(M) в точке M по направлению λ называется предел
Градиент.
Вектор, координатами которого являются значения частных производных функции U(x,y,z) в точке M(x,y,z), называют градиентом функции и обозначают gradU.
gradU — векторная величина.
 
Градиент функции указывает направление наибыстрейшего возрастания функции.
Наибольшая скорость изменения функции U в точке M равна:
33. Ротор, дивергенция векторного поля
Дивергенция векторного поля
Дивергенция характеризует распределение и интенсивность источников и стоков поля.
Дивергенцией (расходимостью) векторного поля
в точке M называется скаляр вида  и обозначается
 .
Дивергенцией векторного поля в точке M называется предел отношения потока поля через замкнутую поверхность S, окружающую точку M, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку M (V -> 0)
Ротор.
Ротором вектора a в точке M называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора а по контуру L плоской площадки S, перпендикулярной этому направлению, к площади этой площадки.
 
34. Оператор Гамильтона.
Векторные операции первого порядка удобно записывать с помощью оператора Гамильтона
Применяя оператор Гамильтона, получим дифф. Операции первого порядка:
1. 
2. 
3. 
35. Потенциальное, гармоническое, соленоидальное поля.
Векторное поле называется соленоидальным, если во всех точках его дивергенция равно нулю.
Свойства:
1. В соленоидальном поле поток вектора через любую замкнутую поверхность равен нулю.
2. Соленоидальное поле является полем ротора некоторого векторного поля, т.е. если div a= 0, то существует такое поле b, что a=rot b. Вектор b называется векторным потенциалом поля а.
3. В соленоидальном поле поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение (интенсивность трубки).
Векторное поле называется потенциальным, если во всех точках поля ротор равен нулю.
Свойства:
1. Циркуляция потенциального поля по любому замкнутому полю в этом контуре равна нулю.
2. В потенциальном поле криволинейный интеграл  вдоль любой кривой L с началом в точке M1 и концом в точке M2 зависит только от положения точек и не зависит от формы кривой.
3. Потенциальное поле является полем градиента некоторой скалярной функции U(x,y,z), т.е. если rot a=0, то существует функция U(x,y,z) такая, что a=gradU.
Векторное поле называется гармоническим, если оно одновременно является потенциальным и соленоидальным (rot a=0 и div a=0).
|
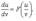
(скалярное поле на (в) трёхмерном пространстве, называемое иногда пространственным полем).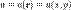
(скалярное поле на (в) двумерном пространстве, называемое иногда плоским полем).
