
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура общего решения ЛНДУСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть дано линейное неоднородное дифференциальное уравнение
Определение. Линейное однородное дифференциальное уравнение
левая часть которого совпадает с левой частью уравнения (1) называется ЛОДУ, соответствующим данному ЛНДУ (1). Теорема 4. Пусть дано уравнение (1) с коэффициентами ► Пусть
Докажем, что (3) является решением ЛНДУ. В силу свойства линейного оператора имеем
а это означает, что Докажем, что (3) является общим решением уравнения (1). Пусть
Дальнейшие рассуждения такие же, как в теореме 3. Задаем произвольные нача- льные условия
ным условиям. Чтобы функция (3) была решением уравнения (1), удовлетворя- ющим начальным условиям (4), должны выполняться следующие равенства:
Система (4) является линейной неоднородной системой уравнений относительно неизвестных Так как начальные условия были произвольными, то можно утверждать, что функция (3) позволяет решать любую задачу Коши, а поэтому (3) – общее решение уравнения (1). ◄
Метод вариации произвольных постоянных Нахождения решения ЛНДУ Метод вариации произвольных постоянных – это есть метод нахождения решения (частного или общего) ЛНДУ, если известна фундаментальная система решений соответствующего ЛОДУ. Он состоит в варьировании произвольных постоянных в общем решении соответствующего ЛОДУ. Рассмотрим метод вариации нахождения решения для ЛНДУ второго порядка. Для линейного уравнения
Пусть дано ЛНДУ
и известна фундаментальная система решений
Общее решение ЛОДУ будет Итак, решение уравнения (1) будем искать в виде:
Нужно подобрать
Очевидно, что производная от этого выражения будет иметь довольно громоздкий вид. Чтобы производная простой вид, полагаем, что
Тогда производные
Подставляя (3), (5) и (6) в уравнение (1), получим
Далее, группируем слагаемые, содержащие
Так как
Равенство (7) является результатом подстановки функции (3) в уравнение (1) Но равенство (7) получено при условии выполнения (4). Итак, чтобы (3) было решением уравнения (1)
Данная система – система неоднородных линейных уравнений относительно неизвестных
есть определитель Вронского, составленный для линейно независимых частных решений точках и система (8) имеет единственное решение Откуда
где
общее решение уравнения (1). Если положить в (9) Для ЛНДУ
где
Общее решение ЛНДУ запишется в виде
Формула Лиувилля Формула Лиувилля позволяет выразить определитель Вронского решений ЛОДУ через коэффициенты уравнения.
Выведем эту формулу для ЛОДУ 2-го порядка:
Пусть
Так как
Будем рассматривать (2) как систему уравнений с неизвестными
Из этой системы найдем
Тогда
Разделяя переменные и интегрируя, получим
Эта формула и называется формулой Лиувилля. Другая запись формулы:
Полагая
Для уравнения формула Лиувилля имеет такой же вид:
где
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.205.123 (0.013 с.) |

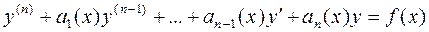 (1)
(1) ( 2)
( 2) ,
, 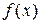 непрерывными на отрезке
непрерывными на отрезке 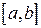 . Общее решение ЛНДУ (1) есть сумма общего решения соответствующего ему ЛОДУ и некоторого частного решения данного ЛНДУ.
. Общее решение ЛНДУ (1) есть сумма общего решения соответствующего ему ЛОДУ и некоторого частного решения данного ЛНДУ.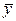 – общее решение ЛОДУ (2),
– общее решение ЛОДУ (2),  – частное решение уравнения (1), тогда общее решение уравнения (1) имеет вид
– частное решение уравнения (1), тогда общее решение уравнения (1) имеет вид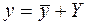 . (3)
. (3) ,
, – решение ЛНДУ.
– решение ЛНДУ. - фундаментальная система решений ЛОДУ (2), тогда решение (3)уравнения (1) примет вид
- фундаментальная система решений ЛОДУ (2), тогда решение (3)уравнения (1) примет вид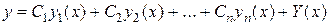 . (3)
. (3)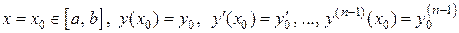 ,
, (4) и покажем, что из (3) при соответствующем подборе произвольных постоянных получается решение, удовлетворяющее этим началь-
(4) и покажем, что из (3) при соответствующем подборе произвольных постоянных получается решение, удовлетворяющее этим началь-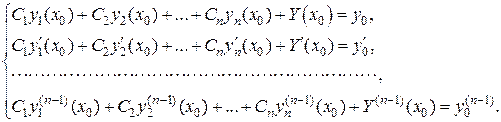 (5)
(5) . Определителем этой системы является определитель Вронского, составленный для функций
. Определителем этой системы является определитель Вронского, составленный для функций 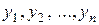 в точке
в точке  . Так как по условию теоремы система функций
. Так как по условию теоремы система функций  , то
, то  имеем
имеем  . Следовательно, система уравнений (5) имеет единственное решение
. Следовательно, система уравнений (5) имеет единственное решение 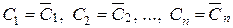 (6). Подставляя (6) в формулу (3), получаем
(6). Подставляя (6) в формулу (3), получаем 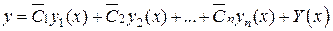 – частное решение, удовлетворяющее заданным начальным условиям (4).
– частное решение, удовлетворяющее заданным начальным условиям (4).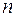 -го порядка сохраняются те же рассуждения.
-го порядка сохраняются те же рассуждения. , (1)
, (1) соответствующего ему ЛОДУ
соответствующего ему ЛОДУ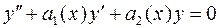 . (2)
. (2) (теорема 3). Так как левые части уравнений (1) и (2) совпадают, то естественно искать решение уравнения (1) в таком же виде, как и решение уравнения (2), немного изменив его, т.е. заменяя произвольные постоянные
(теорема 3). Так как левые части уравнений (1) и (2) совпадают, то естественно искать решение уравнения (1) в таком же виде, как и решение уравнения (2), немного изменив его, т.е. заменяя произвольные постоянные  пока неизвестными функциями
пока неизвестными функциями 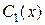 и
и  , которые должны быть дважды дифференцируемыми.
, которые должны быть дважды дифференцируемыми. . (3)
. (3) и
и  таким образом, чтобы (3) было решением уравнения (1). Для этого подставим функцию (3) в уравнение (1). Получим равенство, содержащее неизвестные функции
таким образом, чтобы (3) было решением уравнения (1). Для этого подставим функцию (3) в уравнение (1). Получим равенство, содержащее неизвестные функции  .
. , а следовательно и
, а следовательно и 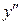 имели более
имели более . (4)
. (4) ,
,  , (5)
, (5) . (6)
. (6)
 и
и  , и выносим их за скобки:
, и выносим их за скобки:
 – решения ЛОДУ (2), то выражения в скобках равны нулю. В итоге получаем равенство
– решения ЛОДУ (2), то выражения в скобках равны нулю. В итоге получаем равенство (7)
(7) (8)
(8) и
и  . Ее определитель
. Ее определитель
 ,
,  .
.
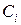 – произвольные постоянные. Подставляя найденные
– произвольные постоянные. Подставляя найденные  в (3), получаем
в (3), получаем (9)
(9) , то получим частное решение ЛНДУ (1).
, то получим частное решение ЛНДУ (1). -го порядка общее решение ищется в виде
-го порядка общее решение ищется в виде ,
, определяются из следующей системы уравнений
определяются из следующей системы уравнений
 .
. – фундаментальная система решений уравнения (1). Вычислим определитель Вронского, составленный для этих функций:
– фундаментальная система решений уравнения (1). Вычислим определитель Вронского, составленный для этих функций: .
. (2)
(2) и
и  :
: (
( )
) ,
, .
.
 ,
,  ,
, . (3)
. (3) .
. , получим
, получим  и формула Лиувилля принимает вид:
и формула Лиувилля принимает вид: .
. го порядка
го порядка 
 ,
, , и получена она может быть с помощью аналогичных рассуждений.
, и получена она может быть с помощью аналогичных рассуждений.


