
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод вариации произвольной постоянной для решения ЛНДУ первого порядка.Содержание книги
Поиск на нашем сайте
Линейному неоднородному дифференциальному уравнению (ЛНДУ) При y=0 дифференциальное уравнение Теперь мы знаем, что Тогда, если подставить Воспользуемся правилом дифференцирования произведения: Производная сложной функции Таким образом, возможен следующий переход: Полученное уравнение есть простейшее дифференицальное уравнение первого порядка. Решив его, мы определим функцию C(x), что позволит записать решение исходного линейного неоднородного дифференциального уравнения первого порядка в виде Подведем итог. Метод вариации произвольной постоянной при решении линейного неоднородного дифференциального уравнения первого порядка состоит из трех этапов: 1. сначала находится общее решение соответствующего ЛОДУ 2. далее варьируется произвольная постоянная С, то есть, заменяется функцией С(x), 3. в заключении функция
Интегрирование ЛОДУ n-го порядка с постоянными коэффициентами Задача нахождения общего решения ЛОДУ n-го порядка (n > 2) с постоянными коэффициентами
где pi, i=1,n, - числа, решается аналогично случаю уравнения второго порядка с постоянными коэффициентами. Сформулируем необходимые утверждения и рассмотрим примеры. Частные решения уравнения (4.6) также ищем в виде у=еkх, где k - постоянное число. Характеристическим для уравнения (4.6) является алгебраическое уравнение n-го порядка вида
Уравнение (4.7) имеет, как известно, n корней (в их числе могут быть и комплексные). Обозначим их через k1, k2,..., kn. Замечание. Не все из корней уравнения (4.7) обязаны быть различными. Так, в частности, уравнение (k-3)2=0 имеет два равных корня: k1=k2=3. В этом случае говорят, что корень один (k=3) и имеет кратность mk=2. Если кратность корня равна единице: mk=1, его называют простым. Случай 1. Все корни уравнения (4.7) действительны и просты (различны). Тогда функции
Пример 4.3. Найти общее решение уравнения Решение: Характеристическое уравнение k3 - 2k2 - К+2=0 имеет корни k1=-1, k2=1, k3=2. Следовательно, Случай 2. Все корни характеристического уравнения действительные, но не все простые (есть корни, имеющие кратность м > 1). Тогда каждому простому корню К соответствует одно частное решение вида екх, а каждому корню k кратности m>1 соответствует m частных решений: еkх, хеkх, х2еkx,..., хm-1еkх. Пример 4.4. Решить уравнение Решение: Характеристическое уравнение
имеет корни k1=-2, k2=1, k3=1, k4=1. Следовательно,
- общее решение уравнения. Случай 3. Среди корней уравнения (4.7) есть комплексно-сопряженные корни. Тогда каждой паре a±β i простых комплексно-сопряженных корней соответствует два частных решения еах cosβx и еах sinβx, а каждой паре а ± βi корней кратности m>1 соответствуют 2m частных решений вида
Эти решения, как можно доказать, образуют фундаментальную систему решений. Пример 4.5. Решить уравнение Решение: Характеристическое уравнение
имеет корни
- общее решение уравнения.
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.147.19 (0.008 с.) |

 соответствует линейное однородное дифференциальное уравнение (ЛОДУ)
соответствует линейное однородное дифференциальное уравнение (ЛОДУ)  (при Q(x) = 0). Дифференциальное уравнение
(при Q(x) = 0). Дифференциальное уравнение 
 при C=0). Таким образом, можно утверждать, что
при C=0). Таким образом, можно утверждать, что  общим решением ЛНДУ.
общим решением ЛНДУ.
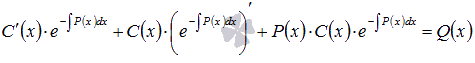
 равна
равна  . А если вспомнить свойства неопределенного интеграла, то
. А если вспомнить свойства неопределенного интеграла, то  .
. .
.

 являются частными решениями уравнения (4.6) и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение уравнения (4.6) записывается в виде
являются частными решениями уравнения (4.6) и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение уравнения (4.6) записывается в виде

 общее решение данного уравнения.
общее решение данного уравнения.



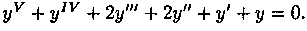

 Следовательно,
Следовательно,



