
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача Коши, формулировка теоремы существования в единственности ее решения. Геометрический смысл ду 1-го порядка, поле направлений, метод изоклинСодержание книги
Поиск на нашем сайте
Задача Коши, формулировка теоремы существования в единственности ее решения. Геометрический смысл ДУ 1-го порядка, поле направлений, метод изоклин Задача отыскания решения ДУ первого порядка P (x; y) dx + Q (x; y) dy = 0, где P (x; y) и Q (x; y) – известные функции, удовлетворяющего заданному начальному условию y (x0) = y0 или y | x = x0 = y0, называется задачей Коши. Теорема существования и единственности решения задачи Коши: если в уравнении y’ = f (x; y) функция f (x; y) и ее частная производная f ’y (x; y) непрерывны в некоторой области D, содержащей точку (x0; y0), то существует единственное решение y = φ (x) этого уравнения, удовлетворяющее начальному условию y (x0) = y0 или y | x = x0 = y0. ДУ первого порядка y’ = f (x; y), разрешенное относительно производной, устанавливает связь (зависимость) между координатами точки (x; y) и угловым коэффициентом y’ касательной к интегральной кривой, проходящей через эту точку. Следовательно, ДУ y’ = f (x; y) дает совокупность направлений (поле направлений) на плоскости Oxy. Таково геометрическое истолкование ДУ первого порядка. Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить y’ = c, т.е. f (x; y) = c.
Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида или уравнение вида Для того, чтобы в уравнении (3.1) разделить переменные, т.е. привести это уравнение к так называемому уравнению с разделенными переменными, произвести следующие действия:
Теперь надо решить уравнение g(y)= 0. Если оно имеет вещественное решение y=a, то y=a тоже будет решением уравнения (3.1). Уравнение (3.2) приводится к уравнению с разделенными переменными делением на произведение
Интегральные кривые (3.3) будут дополнены решениями Пример. Решить уравнение: Решение. Разделяем переменные:
Интегрируя, получаем Далее из уравнений Однородные дифференциальные уравнения 1-го порядка.
Определение 1. Уравнение 1-го порядка Пример 1. Показать, что функция Решение.
что и требовалось доказать. Теорема. Любая функция Доказательство. Первое утверждение теоремы очевидно, т.к. Определение 2. Уравнение в котором M и N – однородные функции одной и той же степени, т.е. обладают свойством Очевидно, что это уравнение всегда может быть приведено к виду Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью замены искомой функции y по формуле y=zx, где z(x) – новая искомая функция. Выполнив эту подстановку в уравнении (4.2), получим: Интегрируя, получаем общий интеграл уравнения относительно функции z(x)
Замечание. Иногда целесообразно вместо указанной выше подстановки использовать подстановку x=zy. Уравнение Бернулли. Определение. Дифференциальное уравнение вида Предполагая, что Введем новую функцию
9. В первом случае линейно независимыми частными решениями заданного дифференциального уравнения оказываются
Функции
не равен нулю для всяких действительных x при
Во втором случае первым частным решением уравнения есть функция Докажем, что
Исходя из того, что k1 = k0 и k2 = k0 являются совпадающими корнями характеристического уравнения, значит, уравнение принимает вид:
Следовательно, Подставив в это уравнение
Т.о.,
Докажем то, что функции
Вывод: линейно независимыми частными решениями линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами
В третьем случае есть два комплексных частных решений линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами
Такие частные решения можно заменить 2-мя действительными функциями
используя формулы из теории функции комплексного переменного вида:
И в подведение итога, обобщим теорию: Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами 10. Линейное неоднородное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами имеет вид Сформулируем теорему, которая показывает в каком виде искать общее решение ЛНДУ. Теорема. Общее решение на интервале X линейного неоднородного дифференциального уравнения Таким образом, общим решением линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами является сумма общего решения соответствующего ЛОДУ второго порядка с постоянными коэффициентами и частного решения исходного ЛНДУ:
Существует несколько методов нахождения частного решения ЛНДУ второго порядка с постоянными коэффициентами. Методы выбираются в зависимости от вида функции f(x), стоящей в правой части уравнения. Перечислим их и разберем решения соответствующих линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
1. Если f(x) является многочленом n-ой степени f(x) = Pn(x), то частное решение ЛНДУ ищется в виде 2. Если функция f(x) представлена произведением многочлена степени n и экспоненты 3 Если функция f(x) имеет вид 4 Если Для любого другого вида функции f(x) применяется следующий алгоритм действий: · находится общее решение соответствующего линейного однородного уравнения как y0 = C1 ⋅ y1 + C2 ⋅ y2, где y1 и y2 - линейно независимые частные решения ЛОДУ, а С1 и С2 – произвольные постоянные; · варьируются произвольные постоянные, то есть, в качестве общего решения исходного ЛНДУ принимается y = C1(x) ⋅ y1 + C2(x) ⋅ y2; · производные функций C1(x) и С2(x) определяются из системы уравнений Подведем итог. Метод вариации произвольной постоянной при решении линейного неоднородного дифференциального уравнения первого порядка состоит из трех этапов: 1. сначала находится общее решение соответствующего ЛОДУ 2. далее варьируется произвольная постоянная С, то есть, заменяется функцией С(x), 3. в заключении функция
Признак Даламбера Если в ряде с положительными членами отношение (n +1)-го члена к n -му при имеет предел l, т.е., то при l > 1 ряд расходится, при l < 1 ряд сходится, при l = 1 ряд может как сходиться, так и расходиться. Признак Коши Пусть дан знакоположительный числовой ряд. Если существует конечный предел, то при l > 1 ряд расходится, при l < 1 ряд сходится, при l = 1 ряд может как сходиться, так и расходиться.
25. Интегральный признак сходимости. Сходимость ряда Теорема. Пусть Доказательство. Ввиду монотонности при всех Пусть теперь наоборот, известно, что ряд сходится. Тогда
Признак Лейбница Для знакочередующихся рядом действует достаточный признак сходимости Лейбница. 1. an+1<an для всех n; 2. limn→∞an=0. Тогда знакочередующиеся ряды ∑n=1∞(−1)nan и ∑n=1∞(−1)n−1an сходятся. Формула Тейлора Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки. Теорема:
30 На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда Этот ряд получил известность благодаря шотландцу Маклорену Разложение Маклорена также называют разложением Тейлора по степеням Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д. Это просто, поскольку при дифференцировании экспонента превращается в саму себя:
Совершенно очевидно, что Подставляем единицы в формулу Маклорена и получаем наше табличное разложение! Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).
Примеры разложения функций в ряд Маклорена В данном параграфе мы рассмотрим типовую задачу на разложение функции в ряд Маклорена и определении области сходимости полученного ряда. Нет, мучаться с нахождением производных не придется, мы будем пользоваться таблицей. Пример 1 Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда. ! Эквивалентная формулировка: Разложить функцию в ряд по степеням
Решение незамысловато, главное, быть внимательным. Конструируем наш ряд. Плясать начинают, как правило, от функции, разложение которой есть в таблице:
В данном случае
Раскрываем наверху скобки: Теперь умножаем обе части на «икс»: В итоге искомое разложение функции в ряд: Как определить область сходимости? Чем постоянно проводить очевидные рассуждения, проще запомнить: разложения синуса, косинуса и экспоненты сходятся при любом действительном значении 31. Определение Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом: ∑n=1∞anxn=a0+a1x+a2x2+…+anxn+… Часто рассматривается также ряд, расположенный по степеням (x−x0), то есть ряд вида ∑n=1∞an(x−x0)n=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…, где x0 − действительное число. Задача Коши, формулировка теоремы существования в единственности ее решения. Геометрический смысл ДУ 1-го порядка, поле направлений, метод изоклин Задача отыскания решения ДУ первого порядка P (x; y) dx + Q (x; y) dy = 0, где P (x; y) и Q (x; y) – известные функции, удовлетворяющего заданному начальному условию y (x0) = y0 или y | x = x0 = y0, называется задачей Коши. Теорема существования и единственности решения задачи Коши: если в уравнении y’ = f (x; y) функция f (x; y) и ее частная производная f ’y (x; y) непрерывны в некоторой области D, содержащей точку (x0; y0), то существует единственное решение y = φ (x) этого уравнения, удовлетворяющее начальному условию y (x0) = y0 или y | x = x0 = y0. ДУ первого порядка y’ = f (x; y), разрешенное относительно производной, устанавливает связь (зависимость) между координатами точки (x; y) и угловым коэффициентом y’ касательной к интегральной кривой, проходящей через эту точку. Следовательно, ДУ y’ = f (x; y) дает совокупность направлений (поле направлений) на плоскости Oxy. Таково геометрическое истолкование ДУ первого порядка. Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить y’ = c, т.е. f (x; y) = c.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.255.239 (0.014 с.) |

 (3.1)
(3.1) (3.2)
(3.2)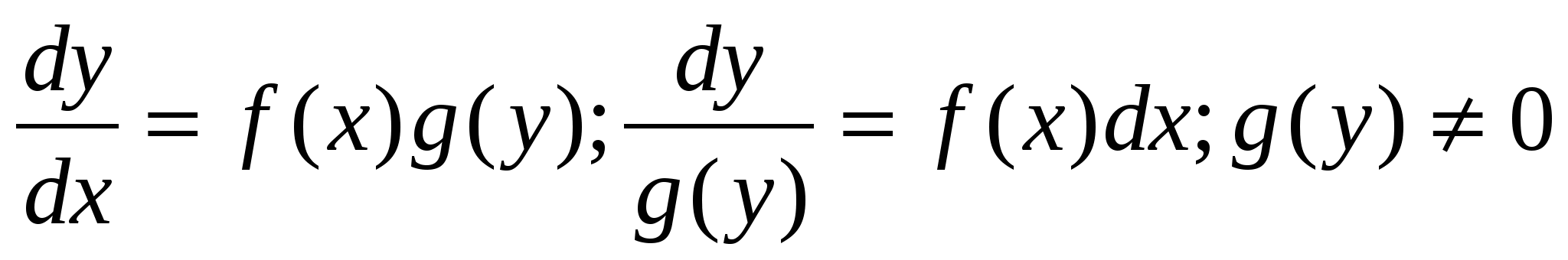
 ;
; :
: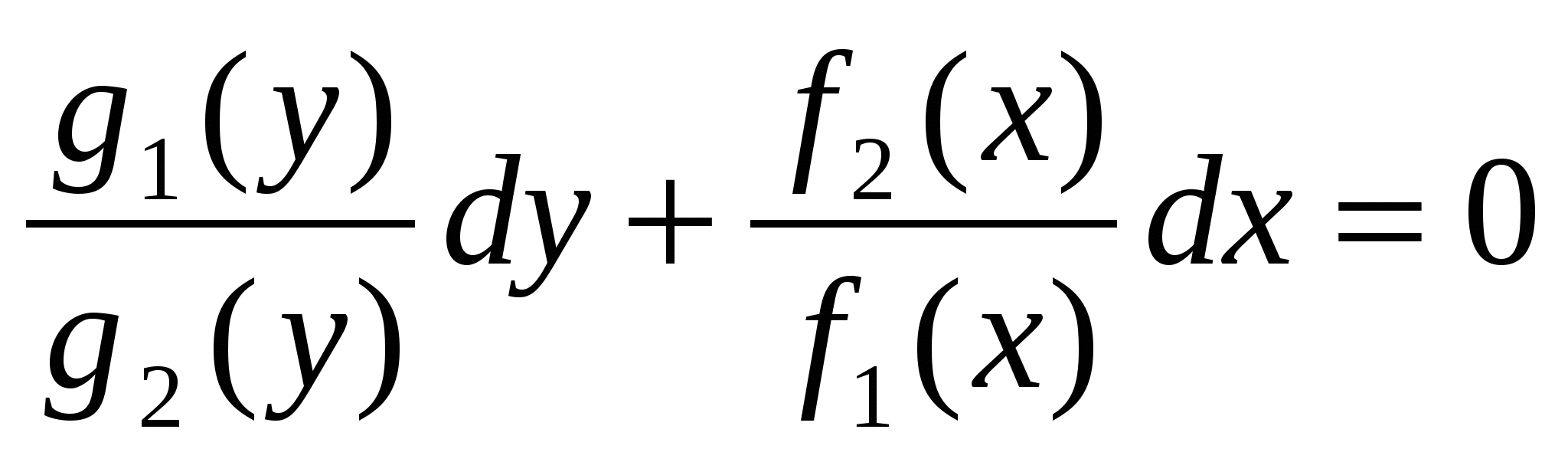 , что позволяет получить общий интеграл уравнения (3.2):
, что позволяет получить общий интеграл уравнения (3.2):  . (3.3)
. (3.3) , если такие решения существуют.
, если такие решения существуют. .
.
 .
.
 и
и 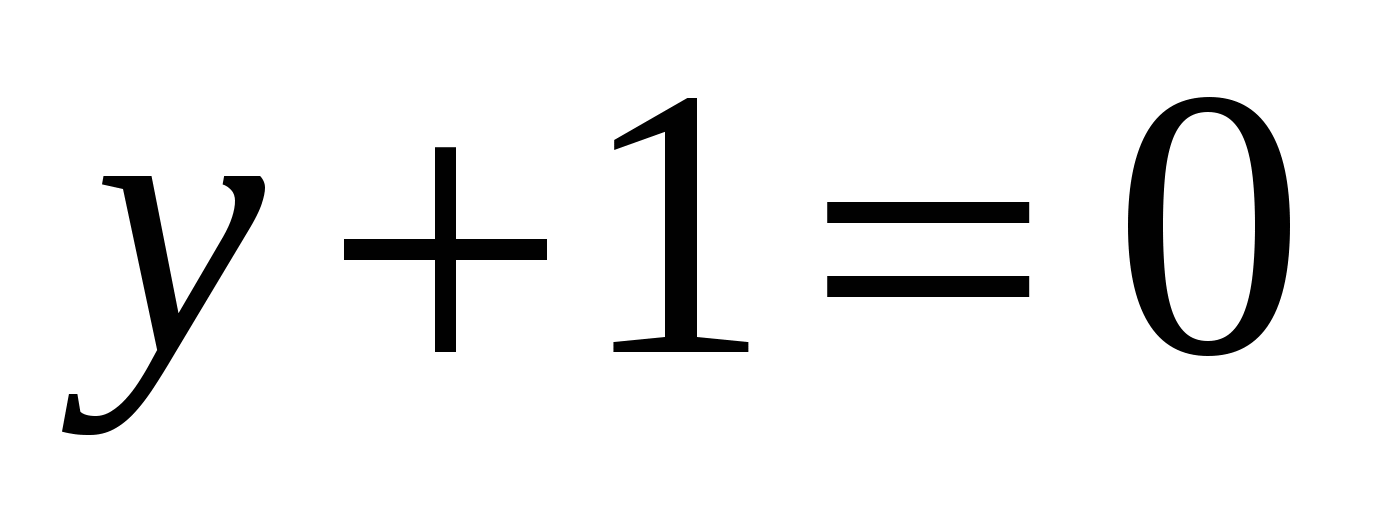 находим x=1, y=-1. Эти решения – частные решения.
находим x=1, y=-1. Эти решения – частные решения. называется однородным, если для его правой части при любых
называется однородным, если для его правой части при любых  справедливо соотношение
справедливо соотношение  , называемое условием однородности функции двух переменных нулевого измерения.
, называемое условием однородности функции двух переменных нулевого измерения. - однородная нулевого измерения.
- однородная нулевого измерения.

 - однородна и, наоборот, любая однородная функция
- однородна и, наоборот, любая однородная функция  нулевого измерения приводится к виду
нулевого измерения приводится к виду  .
. . Докажем второе утверждение. Положим
. Докажем второе утверждение. Положим 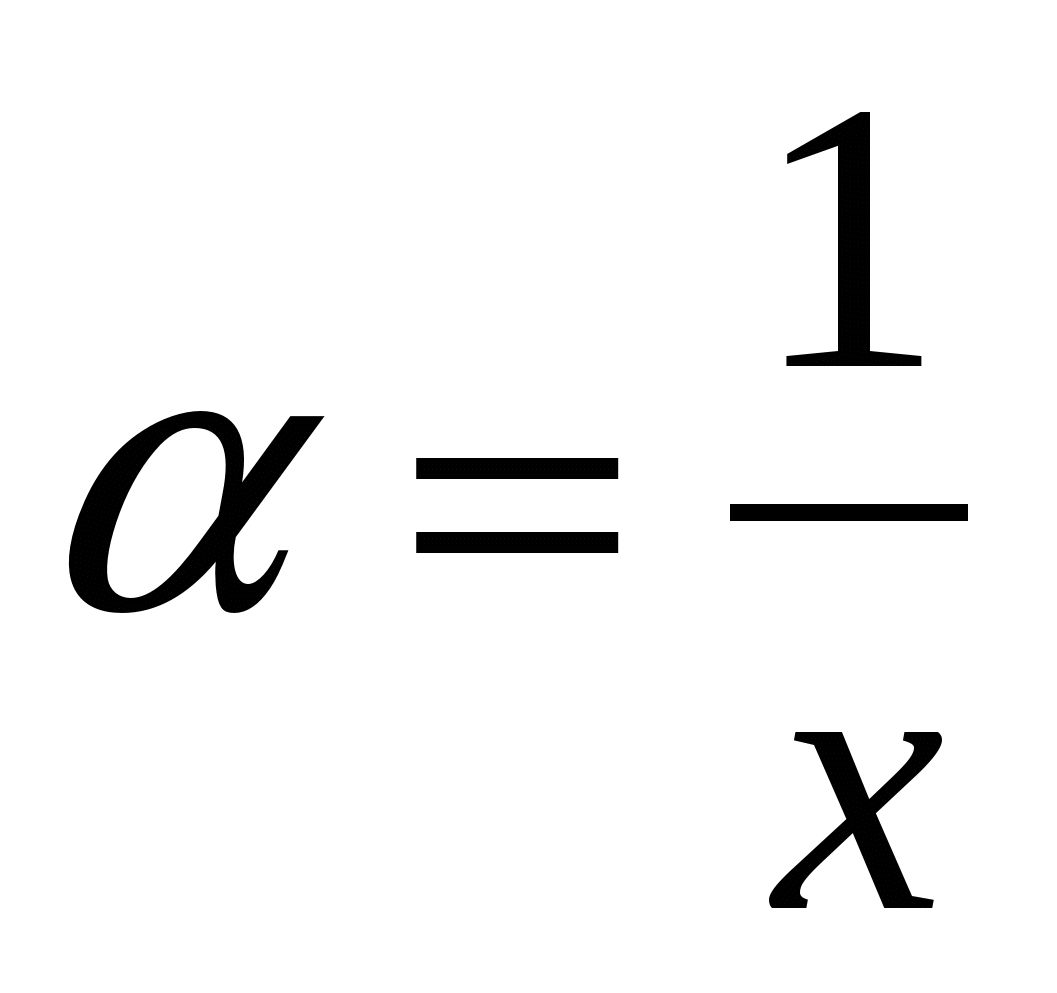 , тогда для однородной функции
, тогда для однородной функции  , что и требовалось доказать.
, что и требовалось доказать. (4.1)
(4.1) при всех
при всех  , называется однородным.
, называется однородным. (4.2), хотя для его решения можно этого и не делать.
(4.2), хотя для его решения можно этого и не делать. или
или 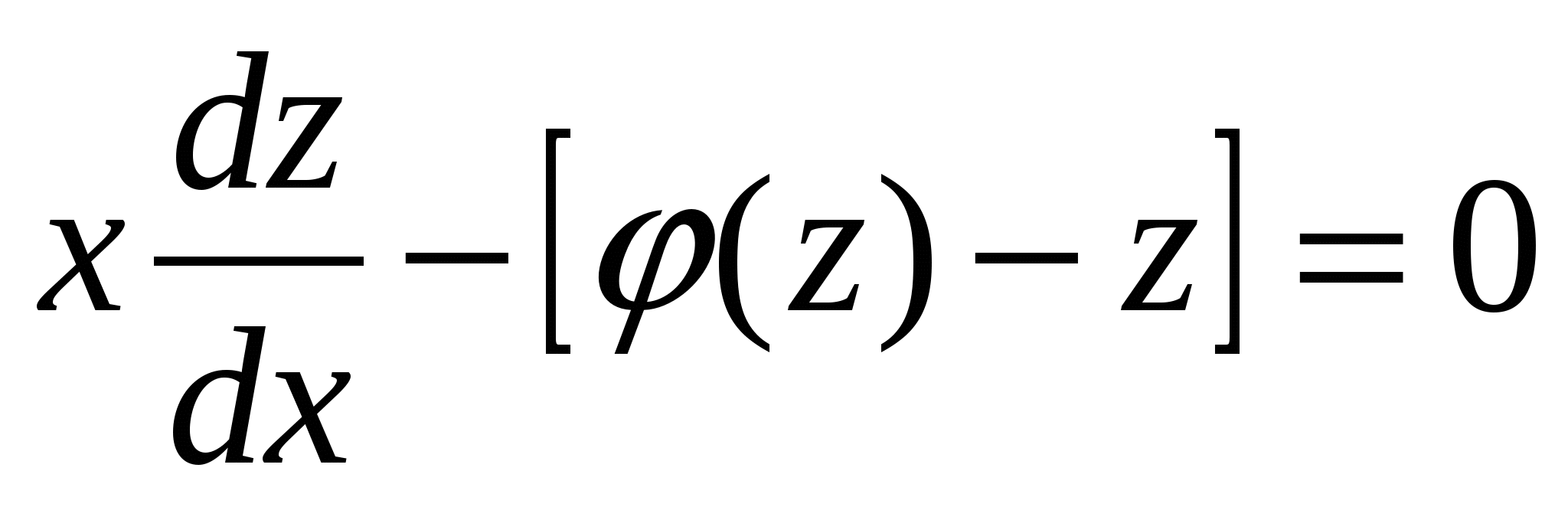 или
или  .
.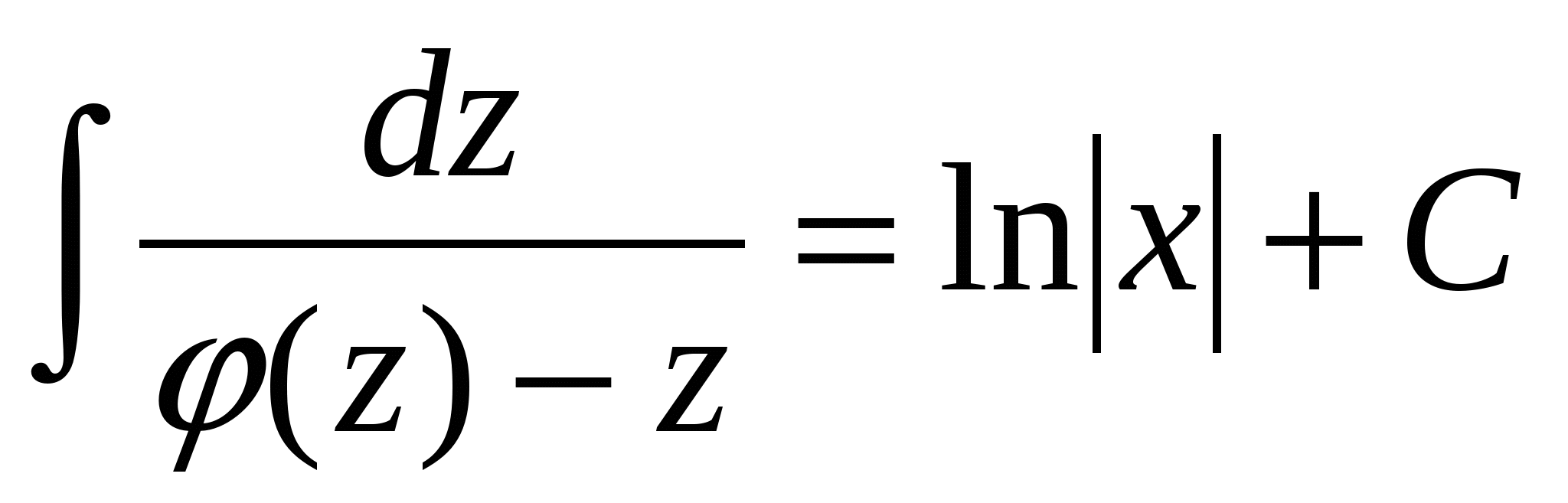 , который после повторной замены
, который после повторной замены  дает общий интеграл исходного уравнения. Кроме того, если
дает общий интеграл исходного уравнения. Кроме того, если  - корни уравнения
- корни уравнения 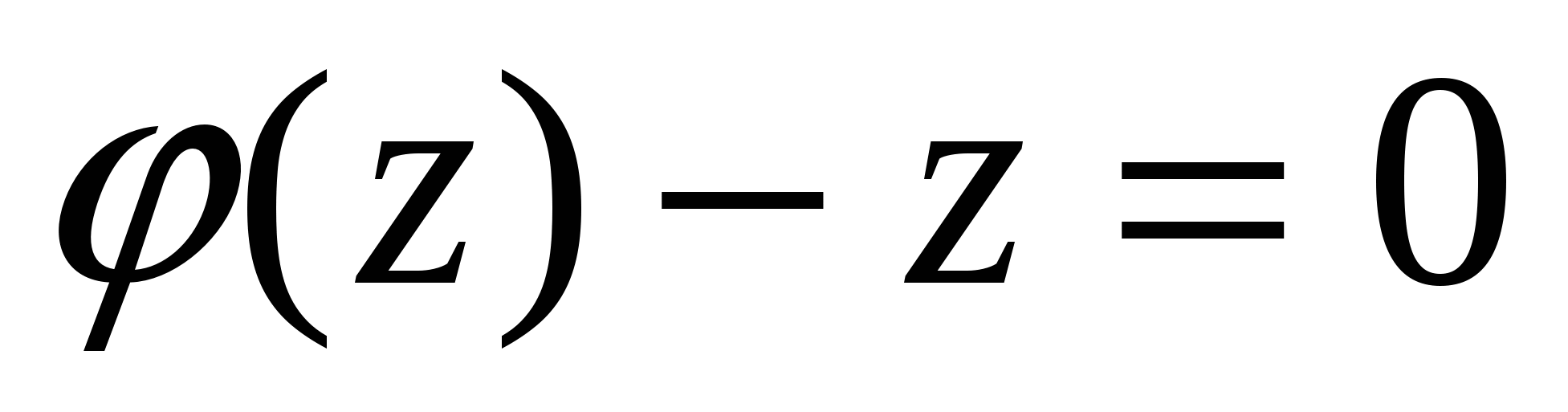 , то функции
, то функции  - решения однородного заданного уравнения. Если же
- решения однородного заданного уравнения. Если же  , то уравнение (4.2) принимает вид
, то уравнение (4.2) принимает вид и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые:
и становится уравнением с разделяющимися переменными. Его решениями являются полупрямые:  .
. , где
, где  , называется уравнением Бернулли.
, называется уравнением Бернулли. , разделим обе части уравнения Бернулли на
, разделим обе части уравнения Бернулли на  . В результате получим:
. В результате получим:  (8.1)
(8.1) . Тогда
. Тогда  . Домножим уравнение (8.1) на
. Домножим уравнение (8.1) на  и перейдем в нем к функции z(x):
и перейдем в нем к функции z(x):  , т.е. для функции z(x) получили линейное неоднородное уравнение 1-го порядка. Это уравнение решается методами, разобранными в предыдущем параграфе. Подставим в его общее решение вместо z(x) выражение
, т.е. для функции z(x) получили линейное неоднородное уравнение 1-го порядка. Это уравнение решается методами, разобранными в предыдущем параграфе. Подставим в его общее решение вместо z(x) выражение 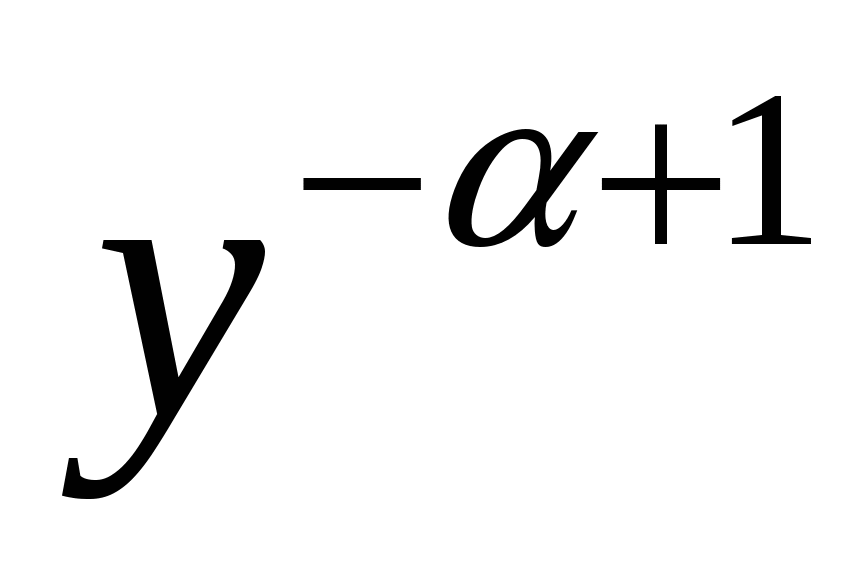 , получим общий интеграл уравнения Бернулли, который легко разрешается относительно y. При
, получим общий интеграл уравнения Бернулли, который легко разрешается относительно y. При  добавляется решение y(x)=0. Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путем подстановки
добавляется решение y(x)=0. Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путем подстановки  , а применяя метод Бернулли, подробно разобранный в § 7. Рассмотрим применение этого способа для решения уравнения Бернулли на конкретном примере.
, а применяя метод Бернулли, подробно разобранный в § 7. Рассмотрим применение этого способа для решения уравнения Бернулли на конкретном примере. и
и 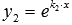 , а общим решением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами оказывается:
, а общим решением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами оказывается: .
.
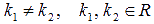 .
. . Вторым частным решением берут
. Вторым частным решением берут  .
. и произведем доказательство линейной независимости y1 и y2.
и произведем доказательство линейной независимости y1 и y2. .
. - исходное ЛОДУ.
- исходное ЛОДУ.

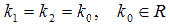 .
. и
и  . Общее решение записываем так:
. Общее решение записываем так: .
. и
и  , которые соответствуют действительной и мнимой частям. Преобразовав общее решение уравнения это можно легко заметить:
, которые соответствуют действительной и мнимой частям. Преобразовав общее решение уравнения это можно легко заметить: ,
, :
:
 , где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.
, где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X. с непрерывными на интервале интегрирования X коэффициентами
с непрерывными на интервале интегрирования X коэффициентами  и непрерывной функцией f(x) равно сумме общего решения
и непрерывной функцией f(x) равно сумме общего решения 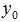 соответствующего ЛОДУ и какого-нибудь частного решения
соответствующего ЛОДУ и какого-нибудь частного решения 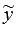 исходного неоднородного уравнения, то есть,
исходного неоднородного уравнения, то есть,  .
. , где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как
, где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как  .
. , то частное решение ЛНДУ второго порядка ищется в виде
, то частное решение ЛНДУ второго порядка ищется в виде  , где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных
, где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных  . Коэффициенты многочлена Qn(x) определяются из равенства
. Коэффициенты многочлена Qn(x) определяются из равенства  , где А1 и В1 – числа, то частное решение ЛНДУ представляется как
, где А1 и В1 – числа, то частное решение ЛНДУ представляется как  , где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных
, где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных  . Коэффициенты многочлена А и В находятся из равенства
. Коэффициенты многочлена А и В находятся из равенства  , то
, то  , где r – число комплексно сопряженных пар корней характеристического уравнения, равных
, где r – число комплексно сопряженных пар корней характеристического уравнения, равных  , Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства
, Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства  , а сами функции C1(x) и C2(x) находятся при последующем интегрировании.
, а сами функции C1(x) и C2(x) находятся при последующем интегрировании. в виде
в виде  ,
, подставляется в исходное дифференциальное уравнение, откуда определяется C(x) и записывается ответ.
подставляется в исходное дифференциальное уравнение, откуда определяется C(x) и записывается ответ.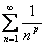
 - непрерывная, неотрицательная, монотонно убывающая функция, определенная при
- непрерывная, неотрицательная, монотонно убывающая функция, определенная при  . Тогда ряд
. Тогда ряд  и интеграл
и интеграл 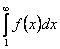 либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся. выполняются неравенства
выполняются неравенства  . Интегрируя, получаем
. Интегрируя, получаем  . Тогда
. Тогда  , или
, или  . Поэтому если
. Поэтому если  . Тогда
. Тогда 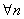
 и
и  ,
,  ряд сходится.
ряд сходится. . Взяв произвольное
. Взяв произвольное  выберем
выберем 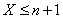 . Тогда
. Тогда  . Значит,
. Значит,  имеет
имеет  производную на отрезке с концами
производную на отрезке с концами  и
и  , то для произвольного положительного числа
, то для произвольного положительного числа  найдётся точка
найдётся точка 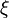 , лежащая между
, лежащая между 
 :
:
 .
.

 , тогда:
, тогда:

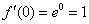






 .
. :
:



 – см. комментарии к табличным разложениям ). Домножение
– см. комментарии к табличным разложениям ). Домножение  на «икс» не играет никакой роли в плане сходимости, поэтому область сходимости полученного ряда:
на «икс» не играет никакой роли в плане сходимости, поэтому область сходимости полученного ряда: 



