
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная и условная сходимостьСодержание книги Поиск на нашем сайте
Ряд ∑n=1∞an называется абсолютно сходящимся, если ряд ∑n=1∞|an| также сходится. 28. Рассмотрим ряды, членами которого являются не числа, а некоторые функции:
¨ Ряды вида (1) называются функциональными. Полагаем, что все функции Ряд (1) может для одних значений “ ¨ Значение ¨ Совокупность значений “”, при которых ряд (1) сходится называется областью сходимости функционального ряда (1). Пример 1. Рассмотрим ряд: Сумма функционального ряда также является некоторой функцией, зависящей от “”:
Так в примере 1: По аналогии числовых рядов введём понятие “
Если для какого–то Известно, что сумма конечного числа слагаемых, каждое из которых есть непрерывная функция, есть функция непрерывная. Производная и интеграл от суммы конечного числа непрерывных функций также равна соответствующей сумме производных и интегралов от этих функций. Можно ли переносить указанные свойства на бесконечное число слагаемых? Можно, но не всегда! 29. Пусть функция
называется рядом Тейлора функции То есть, рядом Тейлора для функции Свойства · Если
· Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке Формула Тейлора Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки. Теорема:
30 На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда Этот ряд получил известность благодаря шотландцу Маклорену Разложение Маклорена также называют разложением Тейлора по степеням Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д. Это просто, поскольку при дифференцировании экспонента превращается в саму себя:
Совершенно очевидно, что Подставляем единицы в формулу Маклорена и получаем наше табличное разложение! Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).
Примеры разложения функций в ряд Маклорена В данном параграфе мы рассмотрим типовую задачу на разложение функции в ряд Маклорена и определении области сходимости полученного ряда. Нет, мучаться с нахождением производных не придется, мы будем пользоваться таблицей. Пример 1 Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда. ! Эквивалентная формулировка: Разложить функцию в ряд по степеням
Решение незамысловато, главное, быть внимательным. Конструируем наш ряд. Плясать начинают, как правило, от функции, разложение которой есть в таблице:
В данном случае
Раскрываем наверху скобки: Теперь умножаем обе части на «икс»: В итоге искомое разложение функции в ряд: Как определить область сходимости? Чем постоянно проводить очевидные рассуждения, проще запомнить: разложения синуса, косинуса и экспоненты сходятся при любом действительном значении 31. Определение Ряд, членами которого являются степенные функции аргумента x, называется степенным рядом: ∑n=1∞anxn=a0+a1x+a2x2+…+anxn+… Часто рассматривается также ряд, расположенный по степеням (x−x0), то есть ряд вида ∑n=1∞an(x−x0)n=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…, где x0 − действительное число.
|
|||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 316; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.115.150 (0.009 с.) |

 (1)
(1) – определены и непрерывны в одном и том же интервале (конечном или бесконечном).
– определены и непрерывны в одном и том же интервале (конечном или бесконечном). ” сходится, для других – расходится.
” сходится, для других – расходится.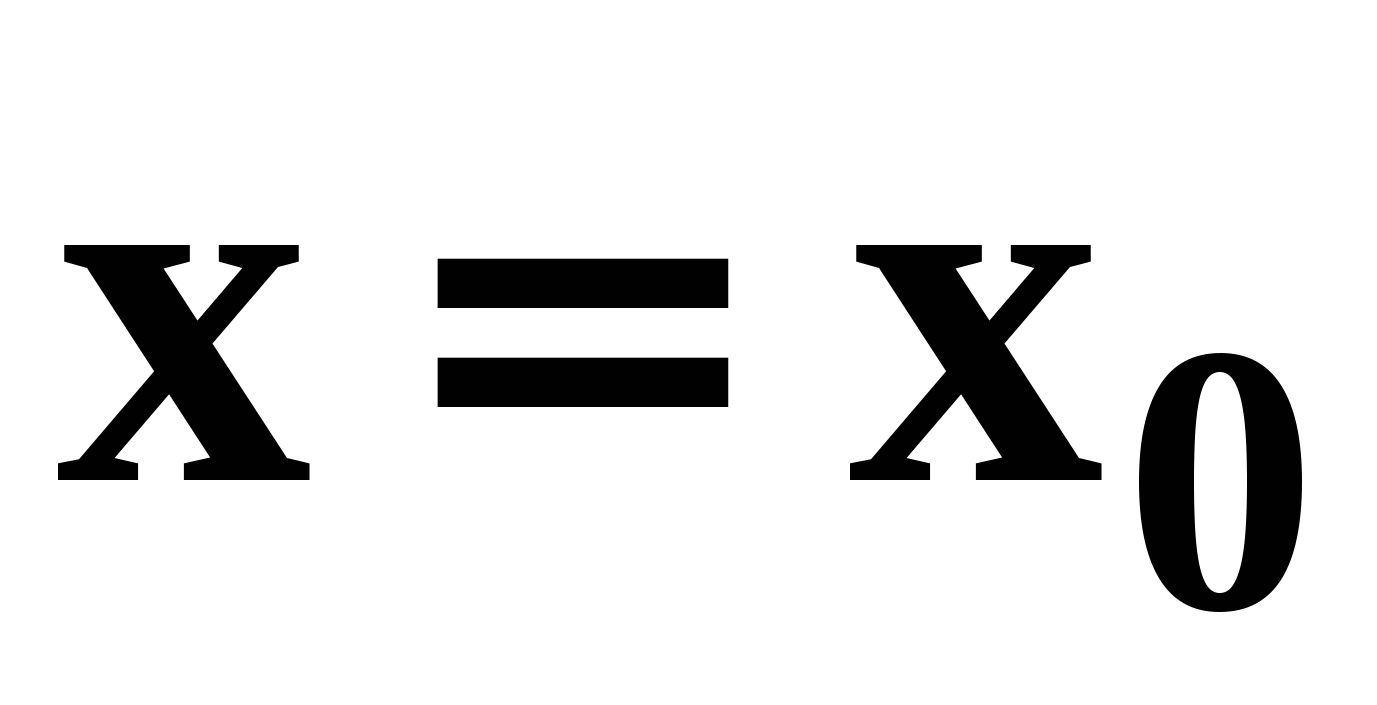 , при котором числовой ряд
, при котором числовой ряд  сходится, называется точкой сходимости функционального ряда (1).
сходится, называется точкой сходимости функционального ряда (1). Если
Если 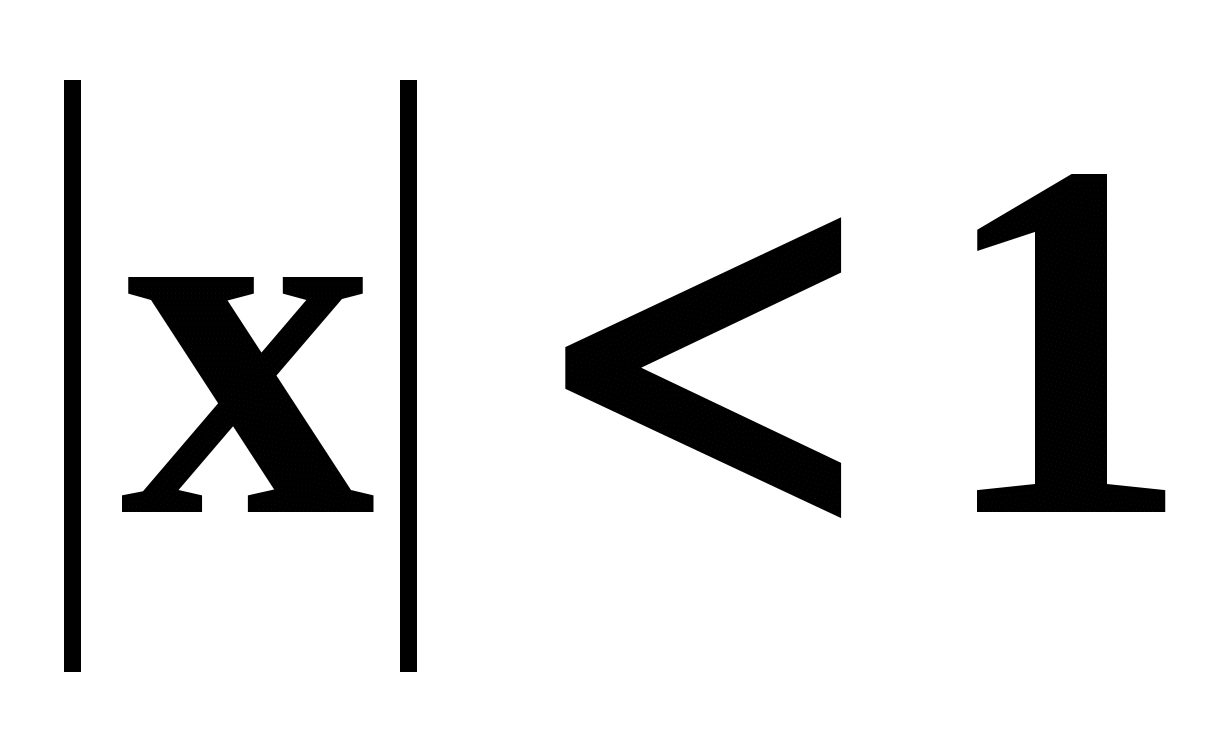 , то данный ряд–это бесконечно убывающая геометрическая прогрессия, и она имеет сумму, равную
, то данный ряд–это бесконечно убывающая геометрическая прогрессия, и она имеет сумму, равную  , где
, где  . Для значений
. Для значений  данный ряд расходится. Отсюда следует, что областью сходимости данного ряда является интервал:
данный ряд расходится. Отсюда следует, что областью сходимости данного ряда является интервал:  .
. .
. , причём эта сумма имеет смысл только при, т.е. в области сходимости данного функционального ряда.
, причём эта сумма имеет смысл только при, т.е. в области сходимости данного функционального ряда. ”–ной частичной суммы ряда (1) и “”– го остатка ряда соответственно:
”–ной частичной суммы ряда (1) и “”– го остатка ряда соответственно: ,
,  .
. (из области сходимости ряда) ряд сходится, то верны равенства:
(из области сходимости ряда) ряд сходится, то верны равенства:  и
и  .
. бесконечно дифференцируема в некоторой окрестности точки
бесконечно дифференцируема в некоторой окрестности точки  . Формальный ряд
. Формальный ряд
 в точке
в точке  вида
вида 

 равны нулю.
равны нулю. производную на отрезке с концами
производную на отрезке с концами  , то для произвольного положительного числа
, то для произвольного положительного числа  найдётся точка
найдётся точка 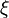 , лежащая между
, лежащая между 
 :
:
 .
.

 , тогда:
, тогда:

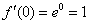






 .
. :
:



 – см. комментарии к табличным разложениям ). Домножение
– см. комментарии к табличным разложениям ). Домножение  на «икс» не играет никакой роли в плане сходимости, поэтому область сходимости полученного ряда:
на «икс» не играет никакой роли в плане сходимости, поэтому область сходимости полученного ряда: 



