
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные дифференциальные уравнения 1-го порядка.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:
где P(x) и Q(x) – заданные непрерывные функции от x. Если функция и называется линейным однородным уравнением, в противном случае Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:
Выражение (7.3) есть общее решение уравнения (7.2). Чтобы найти общее решение уравнения (7.1), в котором функция P(x) обозначает ту же функцию, что и в уравнении (7.2), применим прием, называемый методом вариации произвольной постоянной и состоящий в следующем: постараемся подобрать функцию С=С(x) так, чтобы общее решение линейного однородного уравнения (7.2) являлось бы решением неоднородного линейного уравнения (7.1). Тогда для производной функции (7.3) получим:
Подставляя найденную производную в уравнение (7.1), будем иметь:
или Откуда Первое слагаемое в этой формуле представляет общее решение (7.3) линейного однородного дифференциального уравнения (7.2), а второе слагаемое формулы (7.4) есть частное решение линейного неоднородного уравнения (7.1), полученное из общего (7.4) при Теорема. Если известно одно частное решение линейного неоднородного дифференциального уравнения Однако надо отметить, что для решения линейного неоднородного дифференциального уравнения 1-го порядка (7.1) чаще применяется другой метод, иногда называемый методом Бернулли. Будем искать решение уравнения (7.1) в виде Объединим, например, второе и третье слагаемые последнего выражения и вынесем функцию u(x) за скобку: Потребуем обращения в нуль круглой скобки: Решим это уравнение, полагая произвольную постоянную C равной нулю: Решая его, получим: Следовательно, общее решение уравнения (7.1) имеет вид:
Уравнение Бернулли. Определение. Дифференциальное уравнение вида Предполагая, что Введем новую функцию
9. В первом случае линейно независимыми частными решениями заданного дифференциального уравнения оказываются
Функции
не равен нулю для всяких действительных x при
Во втором случае первым частным решением уравнения есть функция Докажем, что Исходя из того, что k1 = k0 и k2 = k0 являются совпадающими корнями характеристического уравнения, значит, уравнение принимает вид:
Следовательно, Подставив в это уравнение
Т.о.,
Докажем то, что функции
Вывод: линейно независимыми частными решениями линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами
В третьем случае есть два комплексных частных решений линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами
Такие частные решения можно заменить 2-мя действительными функциями
используя формулы из теории функции комплексного переменного вида:
И в подведение итога, обобщим теорию: Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами 10. Линейное неоднородное дифференциальное уравнение (ЛНДУ) второго порядка с постоянными коэффициентами имеет вид Сформулируем теорему, которая показывает в каком виде искать общее решение ЛНДУ. Теорема. Общее решение на интервале X линейного неоднородного дифференциального уравнения Таким образом, общим решением линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами является сумма общего решения соответствующего ЛОДУ второго порядка с постоянными коэффициентами и частного решения исходного ЛНДУ: Существует несколько методов нахождения частного решения ЛНДУ второго порядка с постоянными коэффициентами. Методы выбираются в зависимости от вида функции f(x), стоящей в правой части уравнения. Перечислим их и разберем решения соответствующих линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
1. Если f(x) является многочленом n-ой степени f(x) = Pn(x), то частное решение ЛНДУ ищется в виде 2. Если функция f(x) представлена произведением многочлена степени n и экспоненты 3 Если функция f(x) имеет вид 4 Если Для любого другого вида функции f(x) применяется следующий алгоритм действий: · находится общее решение соответствующего линейного однородного уравнения как y0 = C1 ⋅ y1 + C2 ⋅ y2, где y1 и y2 - линейно независимые частные решения ЛОДУ, а С1 и С2 – произвольные постоянные; · варьируются произвольные постоянные, то есть, в качестве общего решения исходного ЛНДУ принимается y = C1(x) ⋅ y1 + C2(x) ⋅ y2; · производные функций C1(x) и С2(x) определяются из системы уравнений
|
||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |

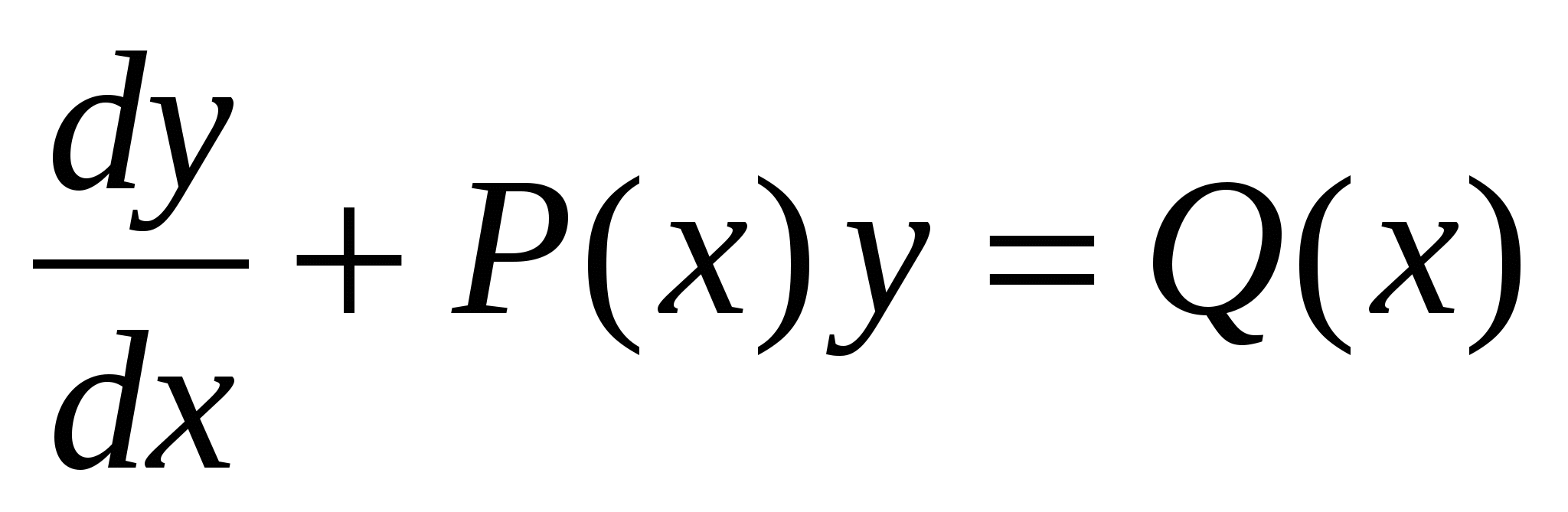 , (7.1)
, (7.1) , то уравнение (7.1) имеет вид:
, то уравнение (7.1) имеет вид:  (7.2)
(7.2)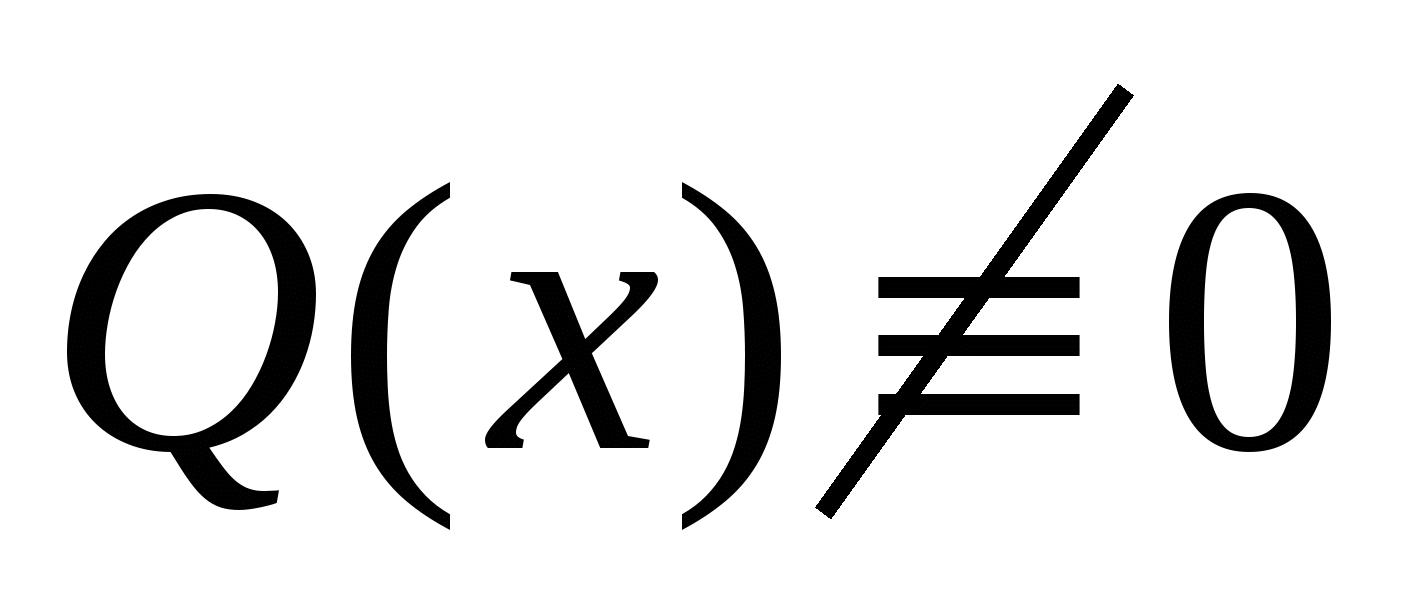 оно называется линейным неоднородным уравнением.
оно называется линейным неоднородным уравнением.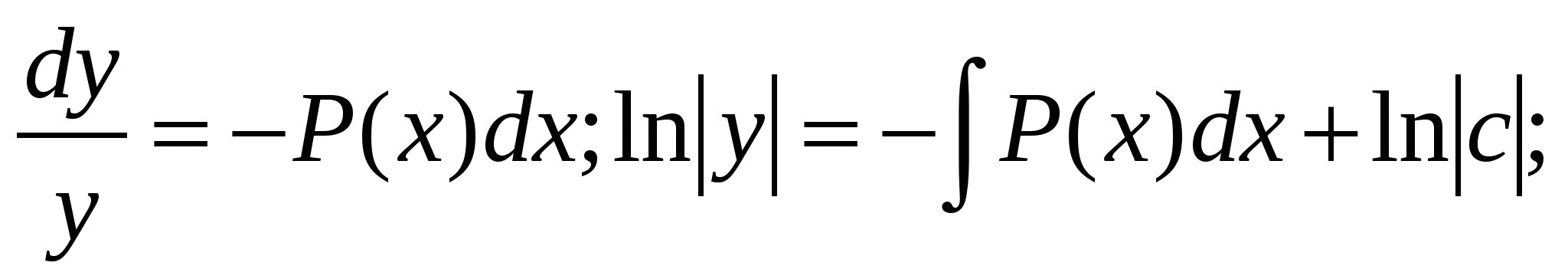
 (7.3)
(7.3) .
.
 .
. , где
, где 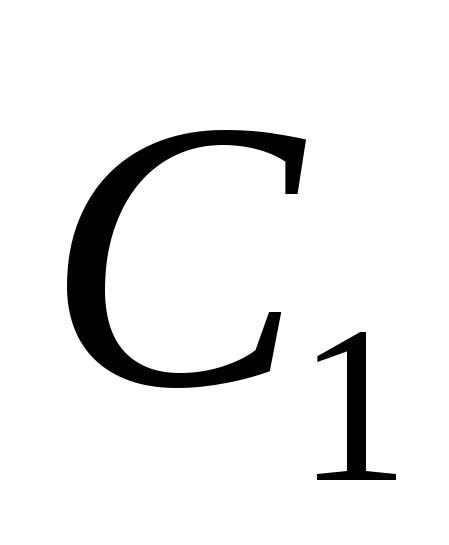 - произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет
- произвольная постоянная. В результате общее решение неоднородного линейного уравнения (7.1) будет 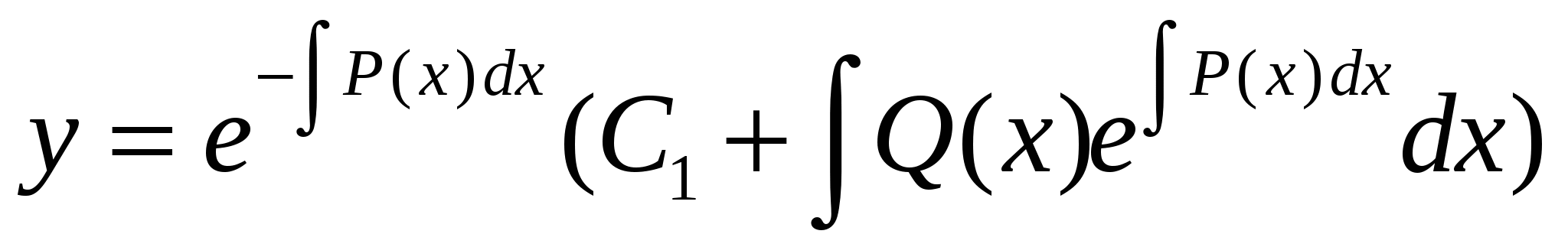 (7.4)
(7.4) 
 . Этот важный вывод выделим в виде теоремы.
. Этот важный вывод выделим в виде теоремы. , то все остальные решения имеют вид
, то все остальные решения имеют вид  , где
, где  - общее решение соответствующего линейного однородного дифференциального уравнения.
- общее решение соответствующего линейного однородного дифференциального уравнения. . Тогда
. Тогда 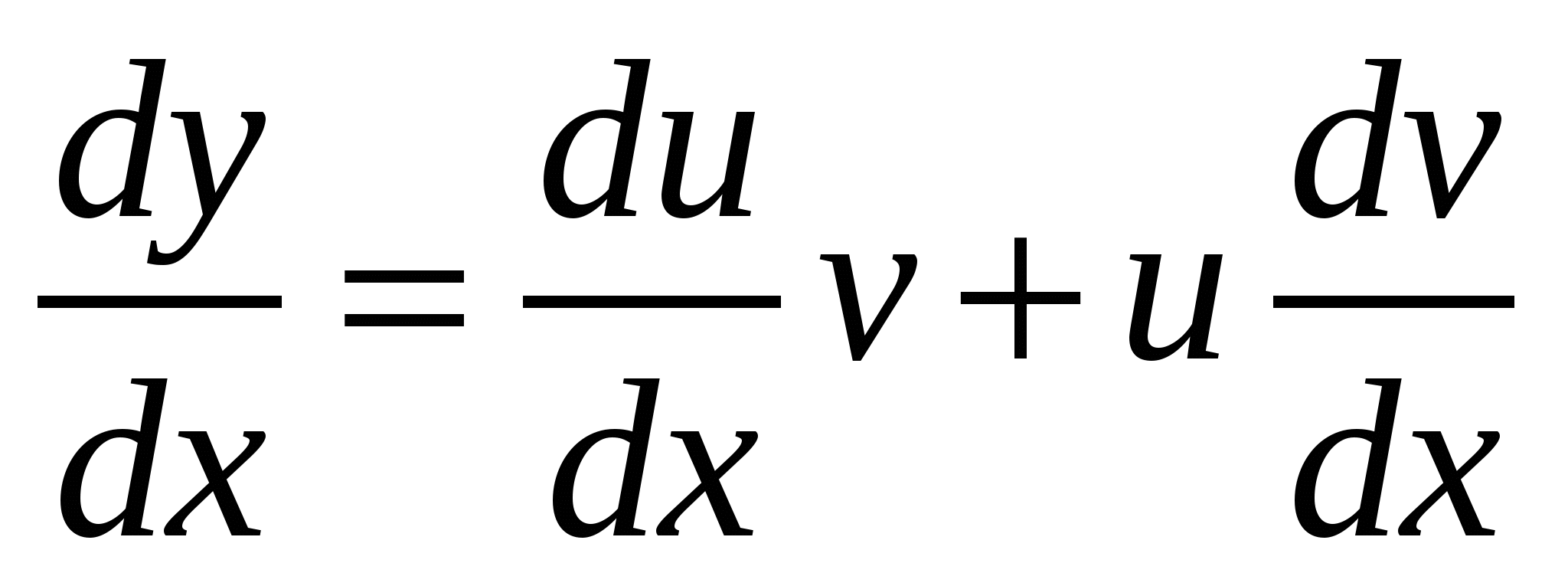 . Подставим найденную производную в исходное уравнение:
. Подставим найденную производную в исходное уравнение:  .
. (7.5)
(7.5) .
.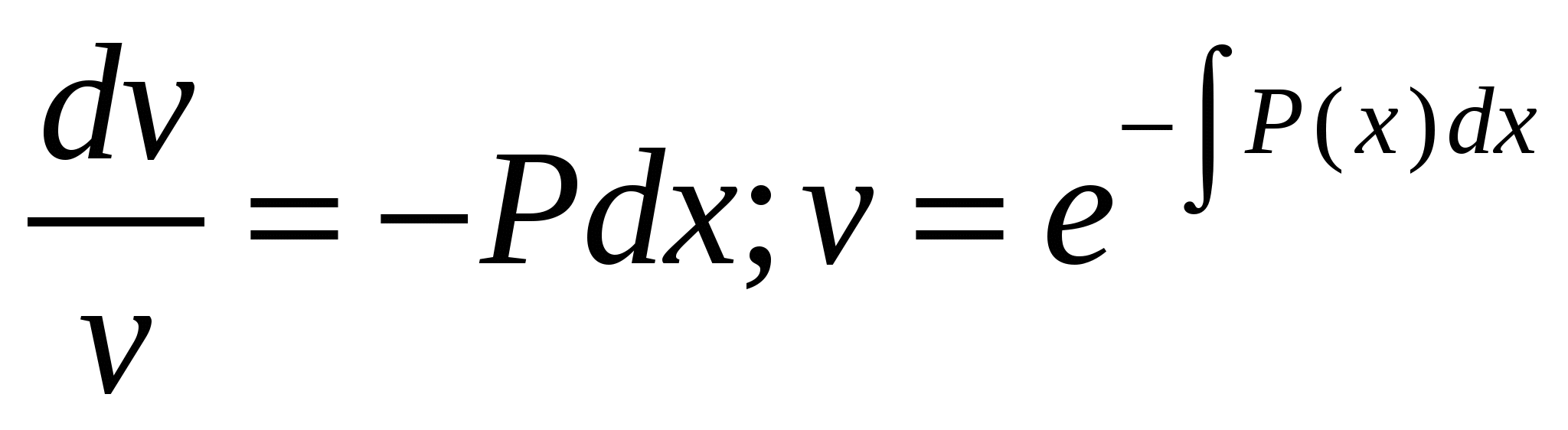 . С найденной функцией v(x) вернемся в уравнение (7.5):
. С найденной функцией v(x) вернемся в уравнение (7.5):  .
. .
. .
. , где
, где  , называется уравнением Бернулли.
, называется уравнением Бернулли. , разделим обе части уравнения Бернулли на
, разделим обе части уравнения Бернулли на  . В результате получим:
. В результате получим:  (8.1)
(8.1) . Тогда
. Тогда  . Домножим уравнение (8.1) на
. Домножим уравнение (8.1) на  и перейдем в нем к функции z(x):
и перейдем в нем к функции z(x):  , т.е. для функции z(x) получили линейное неоднородное уравнение 1-го порядка. Это уравнение решается методами, разобранными в предыдущем параграфе. Подставим в его общее решение вместо z(x) выражение
, т.е. для функции z(x) получили линейное неоднородное уравнение 1-го порядка. Это уравнение решается методами, разобранными в предыдущем параграфе. Подставим в его общее решение вместо z(x) выражение 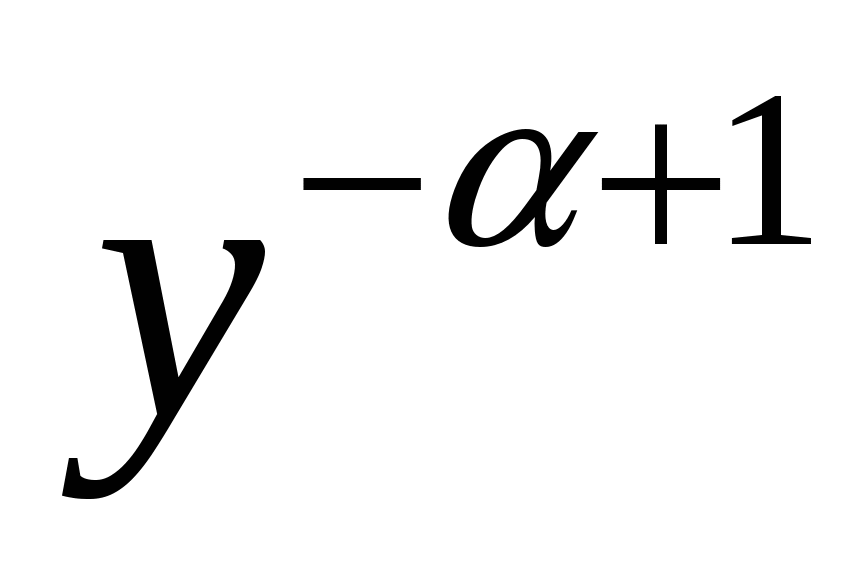 , получим общий интеграл уравнения Бернулли, который легко разрешается относительно y. При
, получим общий интеграл уравнения Бернулли, который легко разрешается относительно y. При  добавляется решение y(x)=0. Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путем подстановки
добавляется решение y(x)=0. Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путем подстановки  , а применяя метод Бернулли, подробно разобранный в § 7. Рассмотрим применение этого способа для решения уравнения Бернулли на конкретном примере.
, а применяя метод Бернулли, подробно разобранный в § 7. Рассмотрим применение этого способа для решения уравнения Бернулли на конкретном примере. и
и 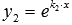 , а общим решением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами оказывается:
, а общим решением линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами оказывается: .
.
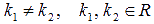 .
. . Вторым частным решением берут
. Вторым частным решением берут  .
. и произведем доказательство линейной независимости y1 и y2.
и произведем доказательство линейной независимости y1 и y2. .
. - исходное ЛОДУ.
- исходное ЛОДУ.

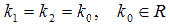 .
. и
и  . Общее решение записываем так:
. Общее решение записываем так: .
. и
и  , которые соответствуют действительной и мнимой частям. Преобразовав общее решение уравнения это можно легко заметить:
, которые соответствуют действительной и мнимой частям. Преобразовав общее решение уравнения это можно легко заметить: ,
, :
:
 , где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X.
, где p и q – произвольные действительные числа, а функция f(x) – непрерывна на интервале интегрирования X. с непрерывными на интервале интегрирования X коэффициентами
с непрерывными на интервале интегрирования X коэффициентами  и непрерывной функцией f(x) равно сумме общего решения
и непрерывной функцией f(x) равно сумме общего решения 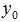 соответствующего ЛОДУ и какого-нибудь частного решения
соответствующего ЛОДУ и какого-нибудь частного решения 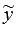 исходного неоднородного уравнения, то есть,
исходного неоднородного уравнения, то есть,  .
. , где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как
, где Qn(x) – многочлен степени n, а r – количество корней характеристического уравнения, равных нулю. Так как  .
. , то частное решение ЛНДУ второго порядка ищется в виде
, то частное решение ЛНДУ второго порядка ищется в виде  , где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных
, где Qn(x) – многочлен n-ой степени, r – число корней характеристического уравнения, равных  . Коэффициенты многочлена Qn(x) определяются из равенства
. Коэффициенты многочлена Qn(x) определяются из равенства  , где А1 и В1 – числа, то частное решение ЛНДУ представляется как
, где А1 и В1 – числа, то частное решение ЛНДУ представляется как  , где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных
, где А и В – неопределенные коэффициенты, r – число комплексно сопряженных пар корней характеристического уравнения равных  . Коэффициенты многочлена А и В находятся из равенства
. Коэффициенты многочлена А и В находятся из равенства  , то
, то  , где r – число комплексно сопряженных пар корней характеристического уравнения, равных
, где r – число комплексно сопряженных пар корней характеристического уравнения, равных  , Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства
, Pn(x), Qk(x), Lm(x) и Nm(x) - многочлены степени n, k, m и m соответственно, m = max(n, k). Коэффициенты многочленов Lm(x) и Nm(x) находятся из равенства  , а сами функции C1(x) и C2(x) находятся при последующем интегрировании.
, а сами функции C1(x) и C2(x) находятся при последующем интегрировании.


