
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные Дифференциальные уравнения первого порядка. Метод вариации.Содержание книги
Поиск на нашем сайте
Линейным дифференциальным уравнением первого порядка называется уравнение вида
Где Замена
Уравнения Бернулли и Дифференциальные уравнения в полных дифференциалах Уравнением Бернулли называется дифференциальное уравнение вида:
Где Замена
Решив уравнение (10) найдем неизвестную функцию Задание 1. Решить уравнение: Решение. Данное уравнение является уравнением с разделяющимися переменными, так как правую часть уравнения можно представить в виде произведения двух функций, каждая из которых зависит только от одной переменной. Перепишем уравнение в виде:
И разделим переменные:
Интегрируем (11):
и получаем общее решение данного уравнения:
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 449; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

 , (7)
, (7) и
и  - заданные непрерывные функции.
- заданные непрерывные функции. , где
, где  - новая неизвестная функция,
- новая неизвестная функция,  - любая первообразная функции
- любая первообразная функции  , преобразует линейное уравнение (7) в уравнение с разделяющимися переменными вида:
, преобразует линейное уравнение (7) в уравнение с разделяющимися переменными вида: . (8) Решив уравнение (8), найдем неизвестную функцию
. (8) Решив уравнение (8), найдем неизвестную функцию 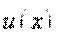 , а, следовательно, и решение уравнения (7):
, а, следовательно, и решение уравнения (7):  .
.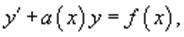 где a (x) и b (x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
· Использование интегрирующего множителя;
· Метод вариации постоянной.
.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
где a (x) и b (x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
· Использование интегрирующего множителя;
· Метод вариации постоянной.
.
Метод вариации постоянной
Данный метод аналогичен предыдущему подходу. Сначала необходимо найти общее решение однородного уравнения:
 Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C (x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C (x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Задача Коши
Если, кроме дифференциального уравнения, задано также начальное условие в форме y (x 0) = y 0, то такая задача называется задачей Коши. Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y (x 0) = y 0.
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C (x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C (x). Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.
Задача Коши
Если, кроме дифференциального уравнения, задано также начальное условие в форме y (x 0) = y 0, то такая задача называется задачей Коши. Решение задачи Коши не содержит произвольной константы C. Ее конкретное числовое значение определяется подстановкой общего решения уравнения в заданное начальное условие y (x 0) = y 0.
 , (9)
, (9) и
и  - заданные непрерывные функции,
- заданные непрерывные функции,  .
. , где
, где  - неизвестная функция,
- неизвестная функция, 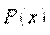 - любая первообразная функции
- любая первообразная функции 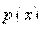 , преобразует уравнение Бернулли в уравнение с разделяющими переменными вида:
, преобразует уравнение Бернулли в уравнение с разделяющими переменными вида: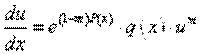 . (10)
. (10)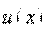 , а, следовательно, и решение уравнения Бернулли (9):
, а, следовательно, и решение уравнения Бернулли (9):  .
.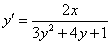 .
.
 . (11)
. (11) ,
, .
. называется уравнением в полных дифференциалах, если существует такая функция двух переменных u (x,y) с непрерывными частными производными, что справедливо выражение
называется уравнением в полных дифференциалах, если существует такая функция двух переменных u (x,y) с непрерывными частными производными, что справедливо выражение
 Общее решение уравнения в полных дифференциалах определяется формулой
Общее решение уравнения в полных дифференциалах определяется формулой
 где C − произвольная постоянная.
Необходимое и достаточное условие
Пусть функции P (x,y) и Q (x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P (x,y) dx + Q (x,y) dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:
где C − произвольная постоянная.
Необходимое и достаточное условие
Пусть функции P (x,y) и Q (x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P (x,y) dx + Q (x,y) dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:
 Алгоритм решения уравнения в полных дифференциалах
1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:
2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u (x,y):
Алгоритм решения уравнения в полных дифференциалах
1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:
2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u (x,y):
 3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:
 4. Дифференцируя по переменной y, подставим функцию u (x,y) во второе уравнение:
4. Дифференцируя по переменной y, подставим функцию u (x,y) во второе уравнение:
 Отсюда получаем выражение для производной неизвестной функции φ (y):
Отсюда получаем выражение для производной неизвестной функции φ (y):
 5. Интегрируя последнее выражение, находим функцию φ (y) и, следовательно, функцию u (x,y):
6. Общее решение уравнения в полных дифференциалах записывается в виде:
5. Интегрируя последнее выражение, находим функцию φ (y) и, следовательно, функцию u (x,y):
6. Общее решение уравнения в полных дифференциалах записывается в виде:
 Примечание: На шаге 3, вместо интегрирования первого уравнения по переменной x, мы можем проинтегрировать второе уравнение по переменной y. После интегрирования нужно определить неизвестную функцию ψ (x)
Примечание: На шаге 3, вместо интегрирования первого уравнения по переменной x, мы можем проинтегрировать второе уравнение по переменной y. После интегрирования нужно определить неизвестную функцию ψ (x)



