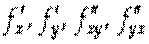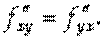Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Градиент, производная по направлению фнп, касательные плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение Градиентом функции Для обозначения градиента функции используется обозначение grad u:
Поскольку единичный вектор
Т. е. имеет форму Скалярного произведения векторов Таким образом, Градиент функции характеризует Направление и Величину максимальной скорости возрастания этой функции в точке. | |||||||||||||
При этом
Обозначение:
Свойства градиента 1. Производная Доказательство. Единичный вектор направления S имеет вид ES ={cosα, cosβ, cosγ}, поэтому правая часть формулы (4.7) представляет собой скалярное произведение векторов grad U и Es, то есть указанную проекцию. 2. Производная в данной точке по направлению вектора S имеет наибольшее значение, равное |grad U |, если это направление совпадает с направлением градиента. Доказательство. Обозначим угол между векторами S И grad U Через J. Тогда из свойства 1 следует, что
Следовательно, ее наибольшее значение достигается при J =0 и равно |grad U |. 3. Производная по направлению вектора, перпендикулярного к вектору grad U, равна нулю. Доказательство. В этом случае
4. Если Z = F (X,Y) – функция двух переменных, то
Направлен перпендикулярно к линии уровня F (X,Y) = C, проходящей через данную точку | ||||||||||||||
:Следовательно, уравнение плоскости можно записать так:
|
Частные производные и дифференциалы высшего порядка
| Дифференциалы высших порядков | 
| 
| 
|
Дифференциалом второго порядка функции U = F (X, Y, Z) называется

 Аналогично можно определить дифференциалы 3-го и более высоких порядков:
Дифференциалом порядка K называется полный дифференциал от дифференциала порядка (K – 1): D KU = D (D K- 1 U).
Свойства дифференциалов высших порядков
1. K -й дифференциал является однородным целым многочленом степени K относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные K -го порядка, умноженные на цело численные постоянные (такие же, как при обычном возведении в степень):
Аналогично можно определить дифференциалы 3-го и более высоких порядков:
Дифференциалом порядка K называется полный дифференциал от дифференциала порядка (K – 1): D KU = D (D K- 1 U).
Свойства дифференциалов высших порядков
1. K -й дифференциал является однородным целым многочленом степени K относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные K -го порядка, умноженные на цело численные постоянные (такие же, как при обычном возведении в степень):
 2. Дифференциалы порядка выше первого не инвариантны относительно выбора переменных
2. Дифференциалы порядка выше первого не инвариантны относительно выбора переменных
| |
Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например, Теорема 3. Если функция Z = F (X,Y) И ее частные производные
определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке
|
Доказательство.
Рассмотрим выражение

И введем вспомогательную функцию

Тогда

Из условия теоремы следует, что J (Х) дифференцируема на отрезке [ X, X+ Δ X ], поэтому к ней можно применить теорему Лагранжа:

Так как в окрестности точки М определена  дифференцируема на отрезке [ Y, Y + Δ Y ], поэтому к полученной разности вновь можно применить теорему Лагранжа:
дифференцируема на отрезке [ Y, Y + Δ Y ], поэтому к полученной разности вновь можно применить теорему Лагранжа:
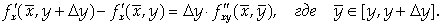
Тогда

Изменим порядок слагаемых в выражении для А:

И введем другую вспомогательную функцию

Проведя те же преобразования, что и для  , получим, что
, получим, что


Следовательно,

В силу непрерывности  и
и 
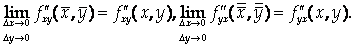 .
.
Поэтому, переходя к пределу при  получаем, что
получаем, что

Что и требовалось доказать.
Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.
|
| Поделиться: |

 задана в некоторой окрестности точки
задана в некоторой окрестности точки  . Рассмотрим некоторое направление, определяемое единичным вектором
. Рассмотрим некоторое направление, определяемое единичным вектором  , где
, где 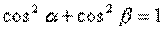 . На прямой, проходящей по этому направлению через точку М, возьмем точку
. На прямой, проходящей по этому направлению через точку М, возьмем точку  ,так что длина отрезка
,так что длина отрезка 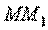 равна
равна  . Приращение функции
. Приращение функции  определяется формулой:
определяется формулой: 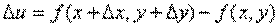 , где
, где  и
и 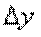 связаны соотношениями
связаны соотношениями  и
и  .
.
 Рис. 6.5.1
Определение
Предел отношения
Рис. 6.5.1
Определение
Предел отношения 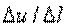 при
при  называется Производной функции по направлению
называется Производной функции по направлению  и обозначается символом
и обозначается символом  :
:
 Если функция
Если функция  дифференцируема в точке
дифференцируема в точке  , то ее приращение в этой точке, с учетом соотношений для
, то ее приращение в этой точке, с учетом соотношений для  и
и 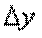 , может быть записана в форме
, может быть записана в форме
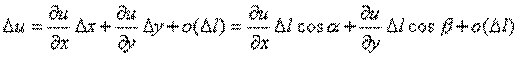 Поделив обе части этого равенства на
Поделив обе части этого равенства на  и переходя к пределу при
и переходя к пределу при  , получаем формулу для производной функции по направлению:
, получаем формулу для производной функции по направлению:
 .
.
 , дифференцируемую в точке
, дифференцируемую в точке 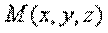 .
. в точке М называется Вектор, координаты которого равны соответственно частным производным
в точке М называется Вектор, координаты которого равны соответственно частным производным  в этой точке.
в этой точке. .
.
 имеет координаты
имеет координаты  , то производная по направлению для случая функции трех переменных запишется в виде
, то производная по направлению для случая функции трех переменных запишется в виде Grad U,
Grad U,
 и grad U.
и grad U. Называется Производной от функции U = F (X, Y, Z) По направлению вектора S и обозначается
Называется Производной от функции U = F (X, Y, Z) По направлению вектора S и обозначается 
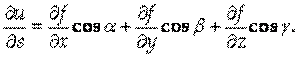

 по направлению некоторого вектора S Равняется проекции вектора grad U на вектор S.
по направлению некоторого вектора S Равняется проекции вектора grad U на вектор S.
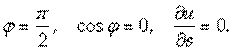

 Плоскость, определяемая этим уравнением, называется Касательной плоскостьюк графику функции Z= F (X, Y) в точке с координатами (х0,у0,Z0).
Плоскость, определяемая этим уравнением, называется Касательной плоскостьюк графику функции Z= F (X, Y) в точке с координатами (х0,у0,Z0).
 ). Докажем это утверждение.
). Докажем это утверждение.