
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная неявной функции нескольких переменных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть непрерывная функция у от х задаётся неявно F (x, y) = 0, где F (x, y), F ' x (x, y), F ' y (x, y) есть непрерывные функции в некоторой области D, содержащей точку (х, у), координаты которой удовлетворяют соотношениям F (x, y) = 0, F ' y (x, y) ≠ 0. Тогда функция у от х имеет производную
Доказательство (смотри рисунок.). Пусть F ' y (x, y) > 0. Так как производная F ' y (x, y) непрерывна, то можно построить квадрат [ х 0 - δ', х 0 + δ', у 0 - δ', у 0 + δ' ], чтобы для всех его точек было F 'y (x, y) > 0, то есть F (x, y) является монотонной по у при фиксированном х. Таким образом, выполнены все условия теоремы существования неявной функции у = f (x), такой, что F (x, f (x)) º 0. Δ F = F (x + Δ x, y + Δ y) − F (x, y) = 0 и в этом случае
где
Из (7) имеем
Так как неявная функция у = f (x) будет непрерывна, то Δ у → 0 при Δ х → 0, значит α → 0 и β → 0. Откуда окончательно имеем
Что и требовалось доказать. Частные производные и дифференциалы высших порядков.
Пусть частные производные
Частные производные второго порядка вида Дифференциалы высших порядков Будем рассматривать dx в выражении для dy как постоянный множитель.Тогда функция dy представляет собой функцию только аргумента x и ее дифференциал в точке x имеет вид (при рассмотрении дифференциала от dy будем использовать новые обозначения для дифференциалов): δ (d y) = δ [ f ' (x) d x ] = [ f ' (x) d x ] ' δ x = f '' (x) d (x) δ x. Дифференциал δ (d y) от дифференциала dy в точке x, взятый при δ x = dx, называется дифференциалом второго порядка функции f (x) в точке x и обозначается d 2 y, т.е. d 2 y = f ''(x)·(dx)2. В свою очередь, дифференциал δ(d 2 y) от дифференциала d 2 y, взятый при δ x = dx, называется дифференциалом третьего порядка функции f (x) и обозначается d 3 y и т.д. Дифференциал δ(d n-1y) от дифференциала dn -1 f, взятый при δ x = dx, называется дифференциалом n - го порядка (или n - м дифференциалом) функции f (x) и обозначается dny. dny = y (n)·(dx) n, n = 1, 2, … (3.1) При доказательстве воспользуемся методом математической индукции. Для n = 1 и n = 2 формула (3.1) доказана. Пусть она верна для дифференциалов порядка n - 1 dn −1 y = y(n −1)·(dx) n −1, и функция y (n -1)(x) дифференцируема в некоторой точке x. Тогда
Полагая δ x = dx, получаем
что и требовалось доказать.
т.е. n - я производная функции y = f (x) в точке x равна отношению n - го дифференциала этой функции в точке x к n - й степени дифференциала аргумента.
Производная по направлению функций нескольких переменных. Рассматривается функция Определение 1. Производная функции u = u (x, y, z) по переменной t называется производной по направлению l Так как на этой прямой u – сложная функция одной переменной, то производная по t равна полной производной по t (§ 12). Она обозначается Градиент функции. Связь между производной по направлению и градиентом функции. Градиентом функции u (х 1, х 2,…, х n) называется вектор, координаты которого равны частным производным функции u: В нашем случае 1. Градиент ортогонален касательной плоскости к поверхности уровня в данной точке. 2. Градиент направлен в сторону максимального роста (изменения) функции в т. М 0. {Этот максимум достигается при φ = 0, т.е. при 3. Величина наибольшей скорости роста функции равна
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 1554; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.185.202 (0.008 с.) |

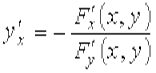 .
.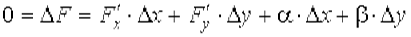 , (7)
, (7)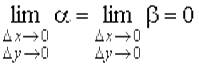 .
.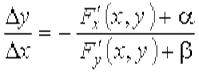 .
. .
.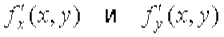 функции z = f (x, y), определенной в окрестности точки М, существуют в каждой точке этой окрестности. В этом случае частные производные представляют собой функции двух переменных х и у, определенные в указанной окрестности точки М. Назовем их частными производными первого порядка. В свою очередь, частные производные по переменным х и у от функций
функции z = f (x, y), определенной в окрестности точки М, существуют в каждой точке этой окрестности. В этом случае частные производные представляют собой функции двух переменных х и у, определенные в указанной окрестности точки М. Назовем их частными производными первого порядка. В свою очередь, частные производные по переменным х и у от функций 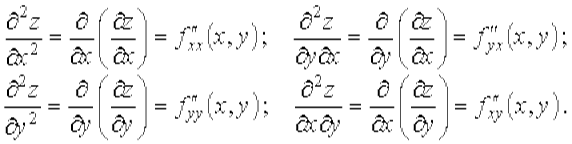
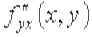 ,
, 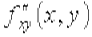 , называются смешенными частными производными.
, называются смешенными частными производными.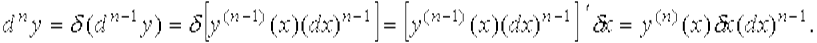
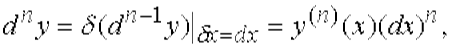
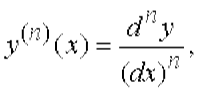 или
или 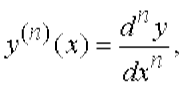
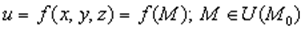 и единичный вектор
и единичный вектор  . Проводится прямая l через т. М 0 с направляющим вектором
. Проводится прямая l через т. М 0 с направляющим вектором 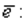

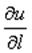 и равна
и равна 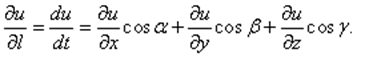
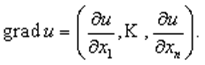
 Таким образом, производная по направлению равна:
Таким образом, производная по направлению равна: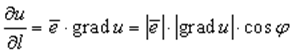 , где φ − угол между направляющим вектором прямой и градиентом функции в данной точке. Отсюда следует геометрический и физический смысл градиента функции (необходимо помнить, что
, где φ − угол между направляющим вектором прямой и градиентом функции в данной точке. Отсюда следует геометрический и физический смысл градиента функции (необходимо помнить, что  скорость изменения функции вдоль прямой l):
скорость изменения функции вдоль прямой l): }
} .
.


