Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непрерывность функции на отрезкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Второй замечательный предел
Следствия 1. 2. 3. 4. 5. 6. Непрерывность функции на отрезке Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках. Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала. Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точкеb. Свойства функций, непрерывных на отрезке Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x Î [a, b] выполняется неравенство |f(x)| ≤ C. Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β Î [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x Î [a, b] Теорема 4 (Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b], то она принимает на (a,b) все промежуточные значения между f(a) и f(b). Свойства Локальные · Функция, непрерывная в точке · Если функция · Если функции · Если функции · Если функция ]Глобальные · Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём. · Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения. · Областью значений функции · Если функция · Если функция · Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна. · Монотонная функция на отрезке · Если функции
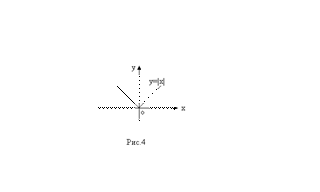
54)Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной —интегрирование. Скорость изменения функции Пусть Вообще производная функции 55) Теплоемкость – есть производная теплоты по температуре, т.е. C(t) = Q/(t) d(l)=m/(l) - линейная плотность K (t) = l /(t) - коэффициент линейного расширения ω (t)= φ/(t) - угловая скорость а (t)= ω/(t) - угловое ускорение N(t) = A/(t) - мощность 56) Связь между дифференцируемостью и непрерывностью функции. Докажем теорему, устанавливающую связь между дифференцируемостью и непрерывностью функции. Теорема 7.1. Если функция y=f(x) дифференцируема в произвольной точке x0, то она непрерывна в этой точке. Доказательство. Пусть функция y=f(x) дифференцируема в произвольной точке x0, т.е. имеет в этой точке производную ∆y = Пусть теперь ∆ x→0. Тогда, очевидно, и ∆y→0. Но это и означает, что функция y=f(x) непрерывна в точке x0. Теорема доказана. Утверждение, обратное этой теореме, неверно: из непрерывности функции в данной точке не вытекает её дифференцируемость в этой точке. Существуют функции, непрерывные в некоторой точке, но не имеющие в этой точке производной. Примером такой функции служит функция y= (см. рис.4).
Эта функция непрерывна в точке x = 0, но не дифференцируема в ней. Действительно, приращение этой функции в точке x = 0 есть ∆y = f(0+∆ x) ─ f(0) = f(∆ x) =
т.е. в любой сколь угодно малой окрестности значения Таблица производных. Гиперболические функции, их свойства и графики. Производные гиперболических и обратных к ним функций. Доказательство Функция y = c принимает значение, равное c для любого аргумента x. Таким образом, Δy = 0 при любом x. Следовательно,
Теорема доказана. Теорема3. Пустьфункции u=u(x), v=v(x) дифференцируемы. Тогда Доказательство Если аргумент x получит приращение Δx, то функции u, v получат приращения
Пусть y=u+v, тогда Воспользовавшись свойством предела суммы функции, получаем
Доказательство. Очевидно, что Dj=Dх (обратная функция непрерывна).Значит
. Если Dх®0, то Dy®0, а поэтому , то есть j'y, что и требовалось доказать. Пример. Пусть y= arcsin x, тогда x= sin y- обратная ê y= arcsin х. Так как , а, то для производной функции y= arcsin x имеем , где учтено что при yÎ[-p/2,p/2], cos y³0. Используя рассмотренные ранее теоремы для других обратных тригонометрических функций имеем: arccos x =p/2- arcsin x и поэтому (arccos x)'=-, y= arctg x, x= tg y, а значит (arctg x)'=, (arcctg x)'=-
60)
Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - вточке u=g(x)! Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга. Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".
Второй замечательный предел
Следствия 1. 2. 3. 4. 5. 6. Непрерывность функции на отрезке Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках. Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала. Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точкеb.
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 2017; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 или
или 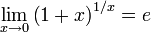
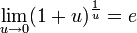
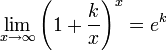
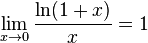
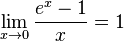
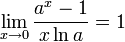 для
для  ,
, 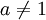

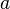 , является ограниченной в некоторой окрестности этой точки.
, является ограниченной в некоторой окрестности этой точки. непрерывна в точке
непрерывна в точке  (или
(или 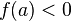 ), то
), то  (или
(или  ) для всех
) для всех 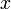 , достаточно близких к
, достаточно близких к 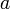 .
.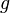 непрерывны в точке
непрерывны в точке 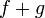 и
и 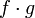 тоже непрерывны в точке
тоже непрерывны в точке 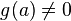 , то функция
, то функция 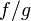 тоже непрерывна в точке
тоже непрерывна в точке 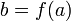 , то их композиция
, то их композиция  непрерывна в точке
непрерывна в точке  , является отрезок
, является отрезок  где минимум и максимум берутся по отрезку
где минимум и максимум берутся по отрезку  то существует точка
то существует точка 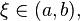 в которой
в которой  .
.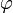 удовлетворяет неравенству
удовлетворяет неравенству 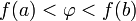 или неравенству
или неравенству  то существует точка
то существует точка 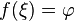 .
. и
и  .
.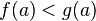 и
и 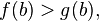 то существует точка
то существует точка 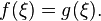 Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.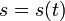 — закон прямолинейного движения. Тогда
— закон прямолинейного движения. Тогда 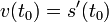 выражает мгновенную скоростьдвижения в момент времени
выражает мгновенную скоростьдвижения в момент времени 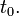 Вторая производная
Вторая производная 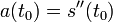 выражает мгновенное ускорение в момент времени
выражает мгновенное ускорение в момент времени  в точке
в точке  выражает скорость изменения функции в точке
выражает скорость изменения функции в точке 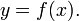
 (x0). Запишем приращение функции ∆y точке x0:
(x0). Запишем приращение функции ∆y точке x0: ∆ x, где
∆ x, где 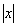 =
= 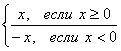
 ,
, =
=  =
= 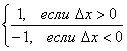 ,
,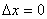 отношение
отношение 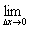




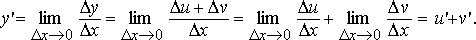
 где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция
где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f. Если f и g - дифференцируемые функции, то сложная функция 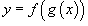 также дифференцируема по x и ее производная равна
также дифференцируема по x и ее производная равна