Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие непрерывности функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Функция f(x), определенная в некоторой окрестности точки a, называется непрерывной в точке а, если Таким образом, функция f непрерывна в точке а, если выполнены следующие условия: 1. функция f определена в некоторой окрестности точки а, т.е. существует число 2. существует 3. A = f(a). Определение непрерывности функции f(x) в точке а, выраженное условием (1), можно сформулировать с помощью неравенств (на языке
Подчеркнем, что в определении непрерывности, в отличие от определения предела, рассматривается полная, а не проколотая окрестность точки а, и пределом функции является значение этой функции в точке а. Назовем разность x – a приращением аргумента и обозначим
При этих обозначениях равенство (1) примет вид Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. По аналогии с понятием предела слева (справа) вводится понятие непрерывности слева (справа). Если функция f определена на полуинтервале Аналогично, если функция f определена на полуинтервале Например, функция f (x) = [ x ] непрерывна справа в точке x = 1 и не является непрерывной слева в этой точке, т.к. f( 1 – 0) = 0, f( 1 + 0) = f( 1 ) = 1. Очевидно, функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке. Точки разрыва. В п.2 будем предполагать, что функция определена в некоторой проколотой окрестности точки а. Точку а назовем точкой разрыва функции f, если эта функция либо не определена в точке а, либо определена, но не является непрерывной в точке а. Следовательно, а – точка разрыва функции f, если не выполняется по крайней мере одно из следующих условий: 1) 2) существует конечный 3) A = f(a). Если а – точка разрыва функции ф, причем в этой точке существуют конечные пределы слева и справа, т.е., то точку а называют точкой разрыва первого рода.
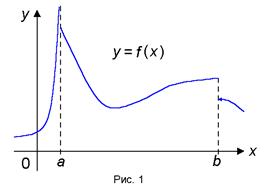
46) Односторонняя непрерывность. Классификация точек разрыва. 5.4.1. Определение односторонней непрерывности. В определении непрерывности функции в точке х0 требуется существование Опр.5.1.7. Функция f(x) называется непрерывной в точке х0 слева, если Опр.5.1.8. Функция f(x) называется непрерывной в точке х0 справа, если 47) Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b. Замечание. Функция, непрерывная на отрезке [ a, b ] может быть разрывной в точках a и b (рис. 1)
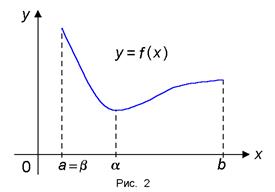
Множество функций, непрерывных на отрезке [ a, b ] обозначается символом C [ a, b ]. Свойства функций, непрерывных на отрезке Теорема 1 (об ограниченности непрерывной функции). Если функция f (x) непрерывна на отрезке [ a, b ], то она ограничена на этом отрезке, т.е. существует такое число C > 0, что " x Î [ a, b ] выполняется неравенство | f (x)| ≤ C. Теорема 2 (Вейерштрасс). Если функция f (x) непрерывна на отрезке [ a, b ], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β Î [ a, b ] такие, что m = f (α) ≤ f (x) ≤ f (β) = M для всех x Î [ a, b ] (рис.2).
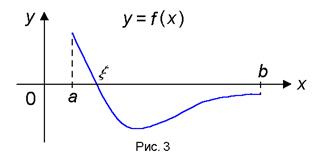
Наибольшее значение M обозначается символом max x Î [ a, b ] f (x), а наименьшее значение m — символом min x Î [ a, b ] f (x). Теорема 3 (о существовании нуля). Если функция f (x) непрерывна на отрезке [ a, b ] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f (ξ) = 0. Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).
Замечание. На этой теореме основан метод приближенного решения уравнения
48)
|
|||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1782; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.70.0 (0.01 с.) |

 (1)
(1)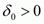 такое, что U
такое, что U 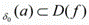 ;
;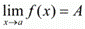 ;
;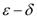 ), с помощью окрестностей и в терминах последовательностей соответственно в виде
), с помощью окрестностей и в терминах последовательностей соответственно в виде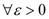
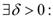
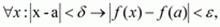

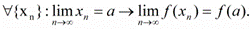
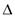 x, а разность f(x) – f(a) – приращением функции, соответствующим данному приращению аргумента
x, а разность f(x) – f(a) – приращением функции, соответствующим данному приращению аргумента  x=x – a,
x=x – a, 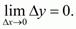
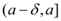 и
и 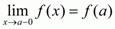 , т.е. f(a – 0) = f(a), то эту функцию называют непрерывной слева в точке а.
, т.е. f(a – 0) = f(a), то эту функцию называют непрерывной слева в точке а. и f(a + 0) = f(a), то эту функцию называют непрерывной справа в точке а.
и f(a + 0) = f(a), то эту функцию называют непрерывной справа в точке а.
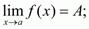
 и равенство
и равенство 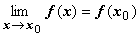 . С применением односторонних пределов определяются понятия непрерывности функции в точке слева и справа:
. С применением односторонних пределов определяются понятия непрерывности функции в точке слева и справа: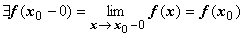 .
.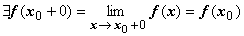 .
.