
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нахождение вектора заданного декартовыми координатами его начальной и конечной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. Так в случае плоской задачи с точками A( x1, y1 ) и B( x2, y2 ) вектор AB = {x2 - x1; y2 - y1}
Найти координаты вектора AB если A(1; 4), B(3; 1). Решение: AB = {3 - 1; 1 - 4} = {2; -3}.
Так в случае пространственной задачи с точками A( x1, y1, z1 ) и B( x2, y2, z2 ) вектор AB = {x2 - x1; y2 - y1; z2 - z1}
Найти координаты вектора AB если A(1; 4; 5), B(3; 4; 2). Решение: AB = {3 - 1; 4 - 4; 2-5} = {2; 0; -3}.
Так как координаты а в декартовой прямоугольной системе координат равны проекциям вектора на координатные оси, то Следует отметить основное свойство направляющих косинусов. Сумма квадратов направляющих косинусов вектора равна единице. Первый способ Пример: дано: вектор а={1, 3, 5). Найти его направляющие косинусы. Второй способ При нахождении направляющих косинусов вектора а, можно использовать методику определения косинусов углов с помощью скалярного произведения. В данном случае в виду имеются углы между а и направляющими единичными векторами прямоугольных декартовых координат i, j и k. Их координаты {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, соответственно. Если угол между векторами ф, то скалярное произведение двух ветров (по определению) – это число, равное произведению модулей векторов на cosф. (a, b) = |a||b|cos ф. Тогда, если b=i, то (a, i) = |a||i|cos(альфа),
20) Скалярное произведение векторов Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними. Скалярное произведение векторов Если угол между векторами
Скалярное произведение
Если векторы
то их скалярное произведение может быть вычислено по формуле
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
Угол
Свойства · теорема косинусов легко выводится с использованием скалярного произведения:
· Угол между векторами:
· Оценка угла между векторами: в формуле · Проекция вектора
· условие ортогональности (перпендикулярности) векторов
· Площадь параллелограмма, натянутого на два вектора
Неравенство Коши — Буняковского Для любых элементов
Скалярное произведение в координатной форме Воспользовавшись свойством скалярного произведения, получим
Скалярное произведение двух векторов в координатной форме равно сумме произведений одноимённых координат:
Косинус угла между двумя векторами Из определения скалярного произведения следует
В координатной форме эта формула примет вид
|
|||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1306; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.163 (0.011 с.) |


 ,
,  обозначается символом
обозначается символом  (порядок записи сомножителей безразличен, то есть
(порядок записи сомножителей безразличен, то есть  ).
).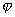 , то их скалярное произведение можно выразить формулой
, то их скалярное произведение можно выразить формулой (1)
(1) называется скалярным квадратом вектора и обозначается символом
называется скалярным квадратом вектора и обозначается символом  . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
. Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля: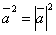 .
.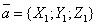 ,
,  ,
, .
. .
.

 знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой. на направление, определяемое единичным вектором
на направление, определяемое единичным вектором  :
: ,
, :
:

 и
и  линейного пространства со скалярным произведением выполняется неравенство [1]
линейного пространства со скалярным произведением выполняется неравенство [1]

 .
. .
. .
. .
.


