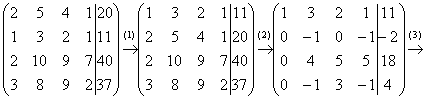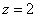Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические показательные формы КЧ.Содержание книги
Поиск на нашем сайте
Сложение комплексных чисел Сложить два комплексных числа Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части: Вычитание комплексных чисел Пример 2 Найти разности комплексных чисел
Действительная часть – составная: Рассчитаем вторую разность: пример с «нехорошей» мнимой частью: Тригонометрические показательные формы КЧ. Умножение комплексных чисел
Деление комплексных чисел Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражения.
Ранг матрицы. Рангом матрицы A r(A) называется наивысший порядок отличных от нуля миноров этой матрицы. Таким образом, ранг матрицы – натуральное число. Ранг нулевой матрицы принимается равным нулю – у нее нет отличных от нуля миноров. Очевидно, что ранг матрицы не превосходит числа ее строк и числа столбцов. Пример. Найти ранг матрицы
Здесь наивысший порядок миноров равен 3 – единственным минором 3-го порядка является определитель матрицы. Но, т. к. 1-я и 3-я строки определителя пропорциональны. Минор второго порядка, полученный выделением 1-й и 2-й строки, 1-го и 3-го столбца
Теорема (о ранге матрицы ступенчатого вида). Ранг матрицы ступенчатого вида равен числу ее ненулевых строк. Пример. Ранг матрицы
равен 3, т. к. у нее 3 ненулевых строки. Отличный от нуля минор максимального порядка в этой матрице можно выбрать, выделив все ее ненулевые строки, а столбцы выделять так, чтобы получился определитель треугольного вида. В рассматриваемом примере это будет определитель
(выбраны 1-й, 2-й, 4-й столбцы). Элементарными преобразованиями матрицы называются: - перестановка двух строк (столбцов) матрицы; - умножение строки (столбца) на число, отличное от нуля; - прибавление к строке (столбцу) другой строки (столбца). Определители второго, третьего и n-того порядков их свойства. Определителем матрицы 2-го порядка
называется число
Пример. Для матрицы
Определителем матрицы 3-го порядка
называется
При вычислении определителей третьего порядка пользуются "правилом треугольников": с плюсом берутся произведения элементов, расположенных на главной диагонали:
Определителем четвертого порядка называется число
Здесь алгебраические дополнения A1j - определители третьего порядка. Используя определитель четвертого порядка, можно аналогичным образом определить определитель пятого, затем шестого и т. д. порядков. Разложение определителя по строке(столбцу). Теорема о разложении определителя по элементам строки (столбца) справедлива для определителей любого порядка. Следовательно, определитель, например, четвертого порядка можно вычислять путем разложения по элементам любой строки или столбца (а не только по элементам первой строки - как в определении). Пример. Вычислить определитель
Разлагая определитель по элементам первого столбца и учитывая, что в нем все элементы, кроме первого, равны нулю, получим
Для вычисления полученного определителя (n–1) - го порядка применим тот же прием. Продолжая этот процесс, окончательно получим
Замечание. Определитель, в котором все элементы ниже (или выше) главной диагонали нулевые, называется определителем треугольного вида. Из примера следует, что определитель треугольного вида равен произведению элементов главной диагонали. 10) 11) Жорданова матрица (нормальная жорданова форма) — одно из фундаментальных понятий линейной алгебры, имеющее большое число приложений в различных разделах математики и физики. Жордановой матрицей называется квадратная блочно-диагональная матрица над полем
при этом каждый блок Для произвольной квадратной матрицы
является жордановой матрицей. При этом матрица
Жорданова форма матрицы определена не однозначно, а с точностью до порядка жордановых клеток. Точнее, две жордановы матрицы подобны над Эквивалентные матрицы Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными. Надо отметить, что равные матрицы и эвивалентные матрицы - понятия совершенно различные. Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.
Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы. Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора. 12) Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением. Здесь > Система (1) называется однородной, если все её свободные члены равны нулю (b 1 = b 2 = … = bm = 0), иначе — неоднородной. > Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. 13) Теорема Кронккера-Копелли: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*. Очевидно, что система (1) может быть записана в виде:
Доказательство. 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга. 2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше. Пример. Определить совместность системы линейных уравнений:
A = ~ Система несовместна.
Пример. Определить совместность системы линейных уравнений.
A* =
14) 14) Решение «СЛАУ» методом Крамера. Теория Рассмотрим систему из n уравнений с n неизвестными:
Вычислим определитель основной матрицы системы:
Обозначим через Δi определитель, получающийся из определителя Δ основной матрицы системы уравнений заменой его i -го столбца столбцом из свободных членов b1,b2,...,bn (с сохранением без изменения всех остальных столбцов).
Квадратная система линейных уравнений с определителем основной матрицы, отличным от нуля, имеет и притом единственное решение, определяемое следующей формулой:
Эта формула называется формулой Крамера, а алгоритм решения системы линейных уравнений - методом Крамера или правилом Крамера. 15)
На первом этапе нужно записать расширенную матрицу системы: Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями. Существуют следующие элементарные преобразования: 1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки: 2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу 3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули. 4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу 5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера:
На практике так подробно, конечно, не расписывают, а пишут короче: Элементарные преобразования не меняют решение системы уравнений ! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя! Вернемся к нашей системе Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке. (2) Делим вторую строку на 3. Цель элементарных преобразований – привести матрицу к ступенчатому виду: В результате элементарных преобразований получена эквивалентная исходной система уравнений: Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса. В нижнем уравнении у нас уже готовый результат: Рассмотрим первое уравнение системы Ответ: Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными. Пример 1 Решить методом Гаусса систему уравнений: Запишем расширенную матрицу системы: Сейчас я сразу нарисую результат, к которому мы придём в ходе решения: Сначала смотрим на левое верхнее число: Теперь первая строка у нас останется неизменной до конца решения. Уже легче. Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах: Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:
Результат записываем во вторую строку: Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3: Результат записываем в третью строку: На практике эти действия обычно выполняются устно и записываются в один шаг: Далее нужно получить единицу на следующей «ступеньке»: В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение: На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь: Для этого к третьей строке прибавляем вторую строку, умноженную на –2: Последнее выполненное действие – причёска результата, делим третью строку на 3. В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений: Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх. В третьем уравнении у нас уже готовый результат: Смотрим на второе уравнение: И, наконец, первое уравнение: Ответ: Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро. Пример 2 Решить систему линейных уравнений методом Гаусса Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока. Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми! Пример 3 Решить систему линейных уравнений методом Гаусса Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак). Дальше алгоритм работает уже по накатанной колее: (2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3. (3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица. (4) К третьей строке прибавили вторую строку, умноженную на 2. (5) Третью строку разделили на 3. Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх: Ответ: Пример 4 Решить систему линейных уравнений методом Гаусса Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения. В последней части рассмотрим некоторые особенности алгоритма Гаусса. Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце. Или еще такой условный пример: Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического. Дождливая осенняя погода за окном.... Поэтому для всех желающих более сложный пример для самостоятельного решения: Пример 5 Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными. Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше. Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса. Желаю успехов! Решения и ответы: Пример 2: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду. Обратный ход: Пример 4: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: Выполненные преобразования: Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы (3) К третьей строке прибавили вторую, умноженную на –1. Обратный ход: Ответ: Пример 5: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: Выполненные преобразования: Обратный ход: Ответ: 16) Вектор – это направленный отрезок. Векторы, лежащие на параллельных прямых, или на одной прямой, называются – компланырными. Компланарные вектора, имеющие одно направление и одну длину – равные. Векторы противоположно направленные и имеющие одну длину – противоположные. Векторы, лежащие в противоположных плоскостях или в одной плоскости – Компланарные. Если точку приложения выбрать произвольно, вектор называется – свободный. Если точка приложения зафиксирована – радиус вектор (связанный вектор). Если точка приложения подчиняется некому закону, то вектор называется – скользящим. 17) Ось – это прямая, на которой указано направление и начало отчета. Орт оси – единичный вектор, имеющий то же направление, что и ось Углом между и (между и осью) называется наименьший, на который надо повернуть один из векторов (ось) до совпадения по направлению с другим вектором. Проекцией на ось называется длина отрезка А`B`, заключенная между ортогональными проекциями начала А и конца В вектора, взятая со знаком (+), если и с (-), если Теорема (о проекции вектора на ось): проекция вектора на ось равна длине этого вектора, умноженной на косинус угла между векторами и осью. Следствие: Равные вектора имеют равные проекции на одну ось. Направленный отрезок называется ортогональной проекцией на ось Теорема (о проекции суммы векторов): проекция суммы двух векторов на ось равна сумме проекций двух векторов на ту же ось. Теорема (о проекции произведения скаляра на вектор): при умножении вектора на скаляр, его проекция на ось умножается на этот же скаляр Пусть в пространстве даны два вектора и. Отложим от произвольной точки O векторы и. Углом между векторами и называется наименьший из углов. Обозначается. Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице). Под углом между вектором и осью l понимают угол между векторами и. Итак, пусть l – некоторая ось и – вектор. Обозначим через A1 и B1 проекции на ось lсоответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l. Тогда проекцией вектора на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора на эту ось. Проекцию вектора на ось l будем обозначать. Ясно, что если угол между вектором и осью l острый, то x2> x1, и проекция x2 – x1> 0; если этот угол тупой, то x2< x1 и проекция x2 – x1< 0. Наконец, если вектор перпендикулярен оси l, то x2= x1 и x2– x1= 0. Таким образом, проекция вектора на ось l – это длина отрезка A1B1, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр. Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор. Рассмотрим некоторые основные свойства проекций. Проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью: Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим. Доказательство. Пусть. Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда. Но. Это свойство можно обобщить на случай любого числа слагаемых. . Доказательство. Пусть угол между вектором и осью. Если λ > 0, то вектор имеет то же направление, что и, и составляет с осью такой же угол. При λ > 0. Если же λ < 0, то и имеют противоположные направления и вектор составляет с осью угол π – φ и. Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.174 (0.015 с.) |

 ,
, 

 и
и  , если
, если 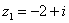


 .
.

 .
.

 Таким образом, r(A) = 2.
Таким образом, r(A) = 2.



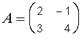
 .
.


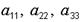 и на треугольниках со сторонами, параллельными главной диагонали; с минусом - произведения элементов побочной диагонали:
и на треугольниках со сторонами, параллельными главной диагонали; с минусом - произведения элементов побочной диагонали:  и на треугольниках, со сторонами, параллельными ей.
и на треугольниках, со сторонами, параллельными ей.



 , с блоками вида
, с блоками вида
 называется жордановой клеткой с собственным значением
называется жордановой клеткой с собственным значением  (собственные значения в различных блоках, вообще говоря, могут совпадать).
(собственные значения в различных блоках, вообще говоря, могут совпадать). над алгебраически замкнутым полем
над алгебраически замкнутым полем 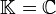 ) всегда существует квадратная невырожденная (т.е. обратимая, с отличным от нуля определителем) матрица
) всегда существует квадратная невырожденная (т.е. обратимая, с отличным от нуля определителем) матрица  над
над 
 называется жордановой формой (или жордановой нормальной формой) данной матрицы
называется жордановой формой (или жордановой нормальной формой) данной матрицы 
 — количество уравнений, а
— количество уравнений, а  — количество неизвестных. x 1, x 2, …, xn — неизвестные, которые надо определить. a 11, a 12, …, amn — коэффициенты системы — и b 1, b 2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
— количество неизвестных. x 1, x 2, …, xn — неизвестные, которые надо определить. a 11, a 12, …, amn — коэффициенты системы — и b 1, b 2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно. + x2
+ x2  + … + xn
+ … + xn 


 .
.  RgA = 2.
RgA = 2. RgA* = 3.
RgA* = 3. А =
А =  ;
;  = 2 + 12 = 14 не равно 0; RgA = 2;
= 2 + 12 = 14 не равно 0; RgA = 2;
 RgA* = 2.
RgA* = 2.
 и решим ее методом Гаусса.
и решим ее методом Гаусса. . По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления. . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае:
. Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: 
 . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:
. В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них:  .
. . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:
. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2:  . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
. Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы. , и ко второй строке прибавляем первую строку умноженную на –2:
, и ко второй строке прибавляем первую строку умноженную на –2:  . Теперь первую строку можно разделить «обратно» на –2:
. Теперь первую строку можно разделить «обратно» на –2:  . Как видите, строка, которую ПРИБАВЛЯ ЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯ ЮТ.
. Как видите, строка, которую ПРИБАВЛЯ ЛИ – не изменилась. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯ ЮТ.

 . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.
. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.
 .
. и подставим в него уже известное значение «игрек»:
и подставим в него уже известное значение «игрек»:
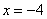


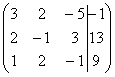



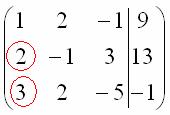
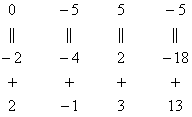










 . Значение «зет» уже известно, таким образом:
. Значение «зет» уже известно, таким образом:

 . «Игрек» и «зет» известны, дело за малым:
. «Игрек» и «зет» известны, дело за малым:






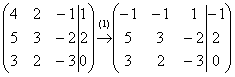

 , и, соответственно,
, и, соответственно, 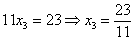 , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.


 .
.

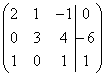
 .
. . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
. Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

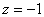
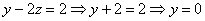

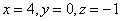 .
.