
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрическая и показательная форма комплексного числаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Любое комплексное число (кроме нуля) Изобразим на комплексной плоскости число
Модулем комплексного числа Модуль комплексного числа По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: Аргументом комплексного числа Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями. Формула Эйлера утверждает, что для любого вещественного числа
где
3) 3) Возведение комплексных чисел в степень Пример Возвести в квадрат комплексное число Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей Второй способ состоит в применение известной школьной формулы сокращенного умножения Для комплексного числа легко вывести свою формулу сокращенного умножения: формула Муавра: Если комплексное число представлено в тригонометрической форме
4) - матрицей называется система m x n чисел, расположенных в прямоугольной таблице, состоящей из m строк и n столбцов. Числа этой таблицы называются – элементами матрицы.
* Аij – элемент матрицы стоящим в ш строке и о столбце. * 2 матрицы называются равными, если они одинаковых размеров и соответственно их элементы равны. * матрица, состоящая из 1 строки – строчная матрица (матрица строка): (А11 А12 … А1n) * матрица, имеющая лишь один столбец – столбцовая матрица:
(А11) (А21) (Аm1) * нулевая матрица:
* Квадратной матрице, называется матрица, у которой число строк совпадает с числом столбцов m=n. * Порядком квадратной матрицы, называется число ее порядков (строк или столбцов). (А11) – кв. матрица 1-го порядка. А11 А22 … А33 – главная диагональ. А1n A2n-1 … An1 – второстепенная диагональ. * Квадратная матрица называется симметричной, если: Аij=Aji
* Диагональной матрицей называется кв. Матрица, у которой все элементы не принадлежащие главной диагонали = 0.
* Матрица называется единичной, если она диагональная и по гл. диагонали все элементы =1. * Символ Кранекера:
* треугольной матрицей, называется кв. матрица, у которой все элементы расположены по одну строку от гл. диагонали = 0. Верхняя треугольная матрица:
* Произвольную матрицу в этом случае, называют квазетреугольной. * Определителем 2-го и 3-го порядка, называется число, равное А11 A22 – A12 A21 │А11 А12│ он так же называется det. │А21 А22│ 5) Умножение матрицы на число
Сложение матриц
6) * Минором какого-либо элемента определителя, называется определитель полученный из данного, вычеркиванием той строки и того столбца, которым принадлежит данный элемент. * Алгебраическим дополнением элемента Аij определ., называется его минор, взятый со знаком (-1)^i+j Aij = (-1)^i+j * Mij > Обратная матрица: * Матрицей обратной кв. матрице А, называется кв. матрица В, удовлетворяющая равенство: АВ=ВА=Е [A^-1 – обратная матрица] * Матрицей присоединенной к матрице А, называется матрица С = (А11 А21 …Аn1) (A12 A22 … An2) … … … (A1n A2n … Ann) , где Aij – алгебраические дополнения матрицы А. * Если А – кв. матрица порядка n, а С – присоединенная к ней матрица, то произведение А*С=С*А=Е*│А│ * Если определитель матрицы А = 0, то матрица называется вырожденной (особенной). Теорема: Для невырожденной матрицы А существует единственная обратная матрица А^-1, определяемая формулой:
А^-1 = 1/│A│ * C Следствие: - Для вырожденной матрицы обратной нет.
Ранг матрицы. Рангом матрицы A r(A) называется наивысший порядок отличных от нуля миноров этой матрицы. Таким образом, ранг матрицы – натуральное число. Ранг нулевой матрицы принимается равным нулю – у нее нет отличных от нуля миноров. Очевидно, что ранг матрицы не превосходит числа ее строк и числа столбцов. Пример. Найти ранг матрицы
Здесь наивысший порядок миноров равен 3 – единственным минором 3-го порядка является определитель матрицы. Но, т. к. 1-я и 3-я строки определителя пропорциональны. Минор второго порядка, полученный выделением 1-й и 2-й строки, 1-го и 3-го столбца
Теорема (о ранге матрицы ступенчатого вида). Ранг матрицы ступенчатого вида равен числу ее ненулевых строк. Пример. Ранг матрицы
равен 3, т. к. у нее 3 ненулевых строки. Отличный от нуля минор максимального порядка в этой матрице можно выбрать, выделив все ее ненулевые строки, а столбцы выделять так, чтобы получился определитель треугольного вида. В рассматриваемом примере это будет определитель
(выбраны 1-й, 2-й, 4-й столбцы). Элементарными преобразованиями матрицы называются: - перестановка двух строк (столбцов) матрицы; - умножение строки (столбца) на число, отличное от нуля; - прибавление к строке (столбцу) другой строки (столбца).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.147 (0.015 с.) |

 можно записать в тригонометрической форме:
можно записать в тригонометрической форме: , где
, где  – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа.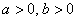 :
: называется расстояние от начала координат до соответствующей точки комплексной плоскости. модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
называется расстояние от начала координат до соответствующей точки комплексной плоскости. модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
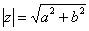 . Данная формула справедлива для любых значений «а» и «бэ».
. Данная формула справедлива для любых значений «а» и «бэ». и радиус-вектором, проведенным из начала координат к соответствующей точке.
и радиус-вектором, проведенным из начала координат к соответствующей точке. выполнено следующее равенство:
выполнено следующее равенство: ,
, — основание натурального логарифма,
— основание натурального логарифма, — мнимая единица.
— мнимая единица.
 и перемножить числа по правилу умножения многочленов.
и перемножить числа по правилу умножения многочленов. :
: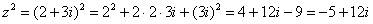
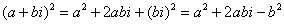 .
. справедлива формула:
справедлива формула:


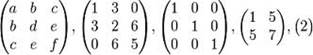




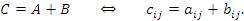



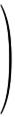

 Таким образом, r(A) = 2.
Таким образом, r(A) = 2.




