
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о комплексных числахСодержание книги Поиск на нашем сайте
Мнимая единица – это число, дающее в квадрате –1:
где Переход от показательной формы к тригонометрической выполняется при помощи формулы Эйлера: Операции над комплексными числами
Сопряженным комплексным числом Если В этой связи следует отметить, что умножение комплексного числа на «–1» означает поворот вектора на Комплексное мгновенное значение может быть представлено с помощью формулы Эйлера в тригонометрической форме При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения, сокращенно их называют комплексными значениями, а соответствующие им векторы на комплексной плоскости – векторами комплексных значений. Связь между комплексом амплитуды и комплексом действующего значения устанавливается по формуле:
Пример символического представления функции времени
Совокупность векторов комплексных значений синусоидальных величин одной частоты, изображенных на комплексной плоскости, называют векторной диаграммой. Пользуясь векторной диаграммой, сложение и вычитание комплексных значений можно заменить сложением и вычитанием соответствующих векторов. Векторные диаграммы, как правило, используются для качественной оценки расчетов и их наглядности. Они являются графическим отображением математических соотношений и расчетов электрической цепи.
Взаимное расположение векторов комплексных значений на векторной диаграмме не изменится, если начальные фазы y всех комплексных значений уменьшить или увеличить на одну и ту же величину. Это означает лишь одновременный поворот всех векторов на один и тот же угол. Часто при анализе цепей векторную диаграмму строят так, чтобы вектор одного комплексного значения был направлен вдоль оси действительных величин. Такой вектор называют исходным вектором. Направления синусоидальных величин (ток, напряжение и др.) в цепи периодически изменяются, но одно из двух направлений выбирается положительным. Это направление выбирается произвольно и показывается стрелкой на схеме соответствующего участка цепи (рис. 3.14). При выбранном положительном направлении синусоидальная величина представляется мгновенным значением Теоремы символического метода 1. Об однозначном соответствии символического изображения данной тригонометрической функции: 2. О линейном преобразовании: если 3. О сумме: если
4. О производной: если 5. Об интеграле: если Таким образом, символический метод позволяет свести дифференциальные уравнения, которыми описываются цепи переменного тока, к виду алгебраических уравнений. Полученное таким образом решение можно затем перевести во временную область.
Законы Ома и Кирхгофа По I закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле электрической цепи, равна нулю, т.е.
В соответствии с теоремой о сумме I закон Кирхгофа в символической или комплексной форме записывается в виде
По II закону Кирхгофа алгебраическая сумма мгновенных значений падений напряжений в замкнутом контуре равна нулю, т.е.
Но в соответствии с теоремами символического метода II закон Кирхгофа в символической или комплексной форме записи имеет следующий вид:
Рассмотрим закон Ома в символической форме записи для элементов цепи гармонического тока (рис. 3.15).
На рис. 3.16 приведены векторные диаграммы напряжений и токов соответственно для сопротивления, индуктивности и емкости.
3.3.3. Последовательное соединение R, L, C
На основании теоремы о сумме
где На основании теоремы Эйлера
Полное сопротивление равно модулю полного комплексного сопротивления Комплексное сопротивление можно представить в виде
где R – действительная часть комплексного сопротивления, называется активным сопротивлением, X – мнимая часть комплексного сопротивления, называется реактивным сопротивлением, Таким образом, закон Ома в общем виде Введем понятие комплексной проводимости Для рассматриваемой цепи построим векторную диаграмму токов и напряжений. Поскольку для всех элементом общим является ток, вектор тока и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.18).
Возможны три режима работы такой цепи:
Угол j(разность начальных фаз напряжения и тока) определяется углом поворота вектора тока к вектору напряжения по кратчайшему пути: если поворот определяется против часовой стрелки, то 3.3.4. Параллельное соединение R, L, C Пусть к цепи, состоящей из параллельного соединения R, L, C элементов (рис. 3.19), приложено напряжение
Согласно теореме о сумме
Применим для каждой ветви закон Ома в комплексной форме:
Тогда где активная проводимость индуктивная проводимость емкостная проводимость На основании формулы Эйлера
Действительная часть комплексной проводимости мнимая часть комплексной проводимости Для рассматриваемой цепи построим векторную диаграмму токов и напряжений. Поскольку для всех элементом общим является напряжение
Возможны три режима работы такой цепи:
Таким образом, в параллельных ветвях характер цепи определяет большая реактивная проводимость или меньшее реактивное сопротивление.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.98.117 (0.009 с.) |

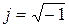 . Введение мнимой единицы дает возможность перейти к комплексному числу (рис. 3.13).
. Введение мнимой единицы дает возможность перейти к комплексному числу (рис. 3.13).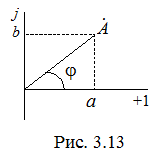 Применяется четыре формы записи комплексного значения синусоидальной величины: полярная, показательная, тригонометрическая и алгебраическая:
Применяется четыре формы записи комплексного значения синусоидальной величины: полярная, показательная, тригонометрическая и алгебраическая: (3.29)
(3.29)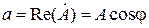 и
и 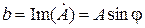 –соответственно действительная и мнимая составляющие комплексного числа;
–соответственно действительная и мнимая составляющие комплексного числа; 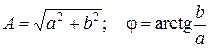 .
.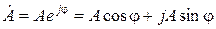 . При значении угла
. При значении угла 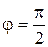 и
и 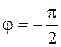 из формулы Эйлера следуют два часто встречающихся соотношения:
из формулы Эйлера следуют два часто встречающихся соотношения: 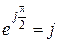 и
и  .
.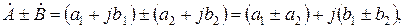

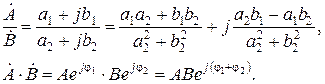
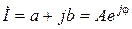 называют число, имеющее противоположный знак фазы или мнимой части
называют число, имеющее противоположный знак фазы или мнимой части 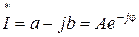 .
. , то
, то 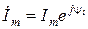 – комплексная амплитуда, а
– комплексная амплитуда, а 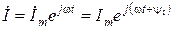 – комплексное изображение мгновенного значения, где
– комплексное изображение мгновенного значения, где 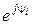 называют фактором поворота, умножение на который означает поворот на угол y i в комплексной плоскости;
называют фактором поворота, умножение на который означает поворот на угол y i в комплексной плоскости; 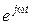 называют фактором вращения, умножение на который означает вращение вектора с постоянной частотой wв положительном направлении вокруг начала координат.
называют фактором вращения, умножение на который означает вращение вектора с постоянной частотой wв положительном направлении вокруг начала координат. , умножение на
, умножение на 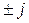 – поворот на
– поворот на 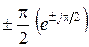 .
. . Интересующая нас функция времени, описывающая изменение тока в цепи, есть мнимая часть мгновенного комплексного значения тока
. Интересующая нас функция времени, описывающая изменение тока в цепи, есть мнимая часть мгновенного комплексного значения тока  :
:  . Именно это соотношение позволяет утверждать, что между мгновенным значением синусоидальной величины и ее символическим изображением существует однозначное соответствие.
. Именно это соотношение позволяет утверждать, что между мгновенным значением синусоидальной величины и ее символическим изображением существует однозначное соответствие.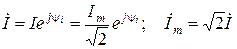 . (3.30)
. (3.30)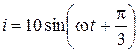 .
.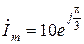 – комплекс амплитуды;
– комплекс амплитуды; – комплекс мгновенного значения;
– комплекс мгновенного значения;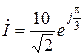 – комплекс действующего значения или комплекс.
– комплекс действующего значения или комплекс.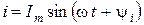 и соответствующим комплексным значением
и соответствующим комплексным значением 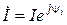 . Следовательно, взаимно однозначному
. Следовательно, взаимно однозначному  представлению синусоидальных токов, напряжений и других величин в виде мгновенных и комплексных значений соответствуют их одинаковые положительные направления.
представлению синусоидальных токов, напряжений и других величин в виде мгновенных и комплексных значений соответствуют их одинаковые положительные направления.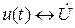 . Это было показано выше:
. Это было показано выше:  , где
, где 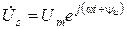 .
.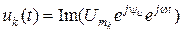 , то
, то 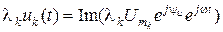 , т.е.
, т.е.  .
. , то
, то 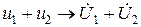 . Следствие:
. Следствие: . Следует отметить, что в правой части складываются векторы по правилам векторной алгебры.
. Следует отметить, что в правой части складываются векторы по правилам векторной алгебры. , а
, а 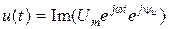 , тогда
, тогда 
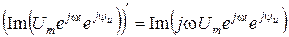 , т.е. взятие производной во временной области означает умножение вектора на j wв комплексной области или поворот вектора на
, т.е. взятие производной во временной области означает умножение вектора на j wв комплексной области или поворот вектора на  :
:  .
.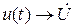 , а
, а  , то
, то 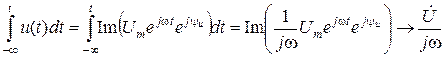 , т.е. интегралу функции во временной области соответствует деление вектора на j wв комплексной области или поворот вектора на угол
, т.е. интегралу функции во временной области соответствует деление вектора на j wв комплексной области или поворот вектора на угол  .
. .
. (3.31)
(3.31) или
или  или
или  . (3.32)
. (3.32) или
или 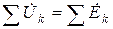 . (3.33)
. (3.33)


 ,
,  (по теореме о линейном преобразовании), то
(по теореме о линейном преобразовании), то 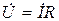 . Это закон Ома в символической форме.
. Это закон Ома в символической форме.

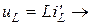
 (по теореме о производной)
Закон Ома:
(по теореме о производной)
Закон Ома:  .
.

 (по теореме об интеграле)
Закон Ома:
(по теореме об интеграле)
Закон Ома:  .
.



 По II закону Кирхгофа
По II закону Кирхгофа .
.
 , (3.34)
, (3.34) – комплексное сопротивление цепи.
– комплексное сопротивление цепи. . (3.35)
. (3.35)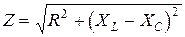 , аргумент полного комплексного сопротивления равен разности фаз напряжения и тока
, аргумент полного комплексного сопротивления равен разности фаз напряжения и тока  .
. (3.36)
(3.36)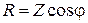 ;
; .
. , где
, где 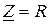 , для индуктивности
, для индуктивности  , для емкости
, для емкости 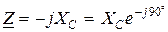 .
. . (3.37)
. (3.37)

 – индуктивный режим,
– индуктивный режим,  ;
; – резонанс напряжений,
– резонанс напряжений,  ;
; – емкостный режим,
– емкостный режим,  .
. , которому соответствует
, которому соответствует  . Определим токи во всех ветвях.
. Определим токи во всех ветвях. По I закону Кирхгофа мгновенное значение тока
По I закону Кирхгофа мгновенное значение тока .
. .
. ,
, ,
, .
. , (3.38)
, (3.38) – полная комплексная проводимость
– полная комплексная проводимость 
 ;
; ;
; ;
; .
. . (3.39)
. (3.39) , называется активной проводимостью;
, называется активной проводимостью; , называется реактивной проводимостью.
, называется реактивной проводимостью. , вектор напряжения и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.20).
, вектор напряжения и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.20).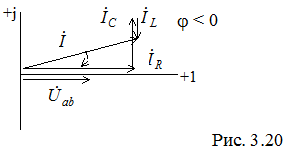

 – индуктивный режим,
– индуктивный режим, 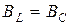 – резонанс токов,
– резонанс токов,  – емкостный режим,
– емкостный режим, 


