
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения мощности в символической формеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вспомним, что мгновенная мощность определяется следующим образом:
Если принять Тогда Мгновенная мощность имеет постоянную составляющую Активная мощность – это постоянная составляющая мгновенной мощности или среднее за период:
Единица измерения мощности – ватт (Вт). Активная мощность всегда положительна. Электрические машины и аппараты конструируют для работы при определенных значениях напряжения и тока, поэтому их характеризуют не активной мощностью, зависящей от сдвига фаз, а полной мощностью
где U, I – действующие значения соответственно напряжения и тока. Полная мощность равна наибольшему значению активной мощности при заданных напряжениях и токах. Также амплитуда гармонической составляющей мгновенной мощности численно равна полной мощности. Размерность полной и активной мощностей одинаковая, однако единицу измерения мощности в применении к полной мощности S называют вольт-ампер ( Отношение активной мощности к полной, равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:
Для эффективного использования электрических машин и аппаратов желательно иметь более высокий коэффициент мощности или меньший сдвиг по фазе тока относительно напряжения, т.е. Высокий коэффициент мощности также желателен для уменьшения потерь при передаче энергии по линиям электропередачи. При данном значении Р приемника ток в линии тем меньше, чем больше При расчетах электрических цепей находит применение реактивная мощность Q:
которая положительна при индуктивном характере цепи (j> 0) и отрицательна при емкостном характере цепи (j < 0). Единицу мощности в применении к измерению реактивной мощности называют вар. Активная, реактивная и полная мощности связаны соотношениями
Как следует из формул, для повышения коэффициента мощности приемника нужно уменьшать его реактивную мощность. В то время, как активная мощность определяет совершаемую работу или передаваемую энергию в единицу времени, полная и реактивная мощности не определяют ни совершаемой работы, ни передаваемой энергии в единицу времени. Однако в электроэнергетике по аналогии с понятием активной мощности приписывают реактивной мощности аналогичный смысл, рассматривают ее как мощность отдачи, получения или передачи некоторой величины, которую хотя она и не является энергией, условно называют реактивной энергией Введем понятие комплексной мощности. Для того чтобы получить полную, активную и реактивную мощности из известных комплексов тока и напряжения, используют следующие соотношения
где Отсюда видно, что действительная часть комплексной мощности равна активной мощности, а мнимая часть – реактивной мощности. Модуль комплексной мощности равен полной мощности S:
Рассмотрим комплексные мощности для различных потребителей: для активного сопротивления:
для индуктивного сопротивления:
для емкостного сопротивления:
Баланс мощности Из закона сохранения энергии следует, что в любой цепи соблюдается баланс как мгновенных, так и активных мощностей. Сумма всех отдаваемых мощностей равна сумме всех получаемых мощностей. Рассмотрим, как соблюдается баланс для комплексных мощностей, а, следовательно, и для реактивных мощностей. Пусть общее число узлов схемы равно n. Запишем для каждого узла уравнение по I закону Кирхгофа для комплексных сопряженных токов:
Эти уравнения записаны в общей форме в предположении, что каждый узел (здесь узел – место соединения не менее двух ветвей) связан с остальными n – 1узлами. При отсутствии каких-либо ветвей соответствующие слагаемые в уравнениях становятся равными нулю. При наличии между какой-либо парой узлов нескольких ветвей число слагаемых соответственно увеличивается. Умножим каждое уравнение (3.59) на комплексный потенциал узла, для которого составлено уравнение:
Просуммируем все уравнения (3.60) с учетом того, что сопряженные комплексные токи входят в эти уравнения дважды (для двух различных направлений), причем
В этом выражении столько слагаемых, сколько ветвей и каждое слагаемое представляет собой комплексную мощность ветви
(3.62) При равенстве сумм комплексных величин суммы их модулей в общем случае не равны друг другу. Отсюда следует, что для полных мощностей S баланс не соблюдается. Метод контурных токов Алгоритм расчета цепей гармонического тока методом контурных токов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.2) с поправкой на символический метод. При решении задачи данным методом составляется система уравнений вида
где
Составим систему уравнений для контурных токов:
где
Метод узловых потенциалов Алгоритм расчета цепей гармонического тока методом узловых потенциалов аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.3) с поправкой на символический метод. При решении задачи данным методом составляется система уравнений вида
где
Для представленной цепи на рис. 3.25 система уравнений вырождается в одно уравнение, поскольку в цепи два узла.
Метод наложения Алгоритм расчета аналогичен рассмотренному при изучении цепей постоянного тока (глава 2.3.4). Рассмотрим применение этого метода на примере схемы на рис. 3.25, которую можно заменить на две составляющие подсхемы (рис. 3.26):
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.200.7 (0.01 с.) |

 .
. , тогда из
, тогда из  следует, что
следует, что  .
. .
. и гармоническую составляющую, изменяющуюся с двойной частотой.
и гармоническую составляющую, изменяющуюся с двойной частотой. (3.49)
(3.49)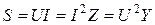 , (3.50)
, (3.50) ).
). (3.51)
(3.51) .
. :
:  .
. (3.52)
(3.52) . (3.53)
. (3.53) (вар×ч), на практике измеряют счетчиками.
(вар×ч), на практике измеряют счетчиками. (3.54)
(3.54) – комплексная мощность,
– комплексная мощность,  – сопряженное значение тока.
– сопряженное значение тока. . (3.55)
. (3.55) (3.56)
(3.56) (3.57)
(3.57) (3.58)
(3.58) (3.59)
(3.59) (3.60)
(3.60) и т.д. В результате получим
и т.д. В результате получим (3.61)
(3.61) . Таким образом, сумма комплексных получаемых мощностей во всех ветвях равна нулю. Полученное равенство выражает баланс мощностей
. Таким образом, сумма комплексных получаемых мощностей во всех ветвях равна нулю. Полученное равенство выражает баланс мощностей  . Из него следует равенство нулю в отдельности суммы определяемых активных и суммы определяемых реактивных мощностей.
. Из него следует равенство нулю в отдельности суммы определяемых активных и суммы определяемых реактивных мощностей. Следует отметить, что взаимное направление токов и напряжений на потребителях и на источниках противоположно, как показано на рис. 3.24. Поскольку отрицательные получаемые мощности представляют собой мощности отдаваемые, то можно утверждать, что суммы всех отдаваемых и всех получаемых реактивных мощностей равны друг другу:
Следует отметить, что взаимное направление токов и напряжений на потребителях и на источниках противоположно, как показано на рис. 3.24. Поскольку отрицательные получаемые мощности представляют собой мощности отдаваемые, то можно утверждать, что суммы всех отдаваемых и всех получаемых реактивных мощностей равны друг другу:  или
или  .
. .
. , (3.63)
, (3.63)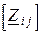 – квадратная матрица комплексных сопротивлений, в которой
– квадратная матрица комплексных сопротивлений, в которой  – собственное комплексное сопротивление,
– собственное комплексное сопротивление, – общее комплексное сопротивление i и j контуров;
– общее комплексное сопротивление i и j контуров; – матрица-столбец контурных токов;
– матрица-столбец контурных токов;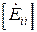 – матрица-столбец контурных ЭДС.
– матрица-столбец контурных ЭДС. Пример. В цепи на рис. 3.25 гармонические источники ЭДС
Пример. В цепи на рис. 3.25 гармонические источники ЭДС



 , (3.63)
, (3.63) – квадратная матрица комплексных проводимостей, в которой
– квадратная матрица комплексных проводимостей, в которой  – собственная комплексная проводимость,
– собственная комплексная проводимость,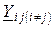 – общая комплексная проводимость ветвей, соединяющих i и j узлы;
– общая комплексная проводимость ветвей, соединяющих i и j узлы; – матрица-столбец потенциалов;
– матрица-столбец потенциалов; – матрица-столбец узловых токов.
– матрица-столбец узловых токов.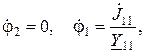





 .
.



