
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение теплового баланса ЭП.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При работе ЭД в различных условиях и при различных нагрузках на его валу изменяются условия протекания тепловых процессов ЭД. Как известно работа ЭД сопровождается потерями мощности а во вторых рассеивается в окружающую среду:
В начале основная часть выделяемого тепла идет на нагревание самого двигателя и значительно меньшая часть отдается в окружающую среду. В процессе нагревания ЭД это соотношение изменяется в сторону 1. Эл.маш. является однородным телом с одинаковой по всему телу теплоёмкостью 2. Теплоотдача в окружающую среду пропорциональна разности температур двигателя и окружающей среды, т.е.:
Чаще всего при анализе тепловых переходных процессов в качестве
С учетом этих допущений, уравнение 3 запишется в виде:
где
теплоёмкость – численно равна количеству тепла, необходимое для нагрева двигателя на 1 градус. теплоотдача- количеству тепла, выделявшему в ОС при изменении температуры на один градус за время равное 1 секунде.
Если
Уравнение (104) описывает тепловые переходные процессы в ЭД и в частном случае для установившегося режима примет вид.
Если в уравнении (104) отношение
(105)- представляет из себя дифференциальное уравнение 1-го порядка и носит название дифференциальное уравнение теплового баланса. При нагреве от некоторого начального значения
Графически это уравнение может быть представлено в виде экспоненциальной функции следующего вида:
Рис.79
В частном случае если включение двигателя происходит в момент когда его температура равна температуре окружающей среды, график будет иметь следующий вид:
Рис.80 Если двигатель в процессе работы нагреть до
Постоянная времени нагрева. Физический смысл Если мы в уравнении (103) условно примем
Уравнение (107) решим относительно времени. за которое при этих условиях двигатель нагреется от
Учитывая, что Таким образом доказали, что физический смысл постоянной времени нагрева соответствует записанному определению нагреву. Для определения постоянной времени нагрева можно использовать решение уравнения теплового баланса в виде:
Примем в уравнении (108)
Поэтому для определения постоянной времени нагрева необходимо экспериментально, построить график
Рис.81 Однако на практике значительно чаще приходиться иметь дело с другими постановками задачи для того чтобы, кривую нагрева, необходимо знать постоянную времени нагрева. Как уже было сказано теплоотдача двигателя.
Рис.82
Необходимо отметить также, что длительность переходного режима при изменении температуры двигателя
Рис.83
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1088; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.165 (0.011 с.) |

 , которые складываются из магнитных потерь (в стали),электрических потерь (потерь в меди), а также механических потерь. За время
, которые складываются из магнитных потерь (в стали),электрических потерь (потерь в меди), а также механических потерь. За время  двигатель с потерями мощности равными
двигатель с потерями мощности равными  . Это тепло во первых расходуется на нагревание самого двигателя:
. Это тепло во первых расходуется на нагревание самого двигателя: (99)
(99) (100)
(100) (101)
(101) и при некоторой температуре двигателя наступает установившийся режим, после чего всё выделяемое при работе тепло рассеивается в окружающую среду., а температура двигателя при условии неизменности нагрузки на его валу в дальнейшем не меняется. Необходимо отметить, что реальные термодинамические процессы в ЭП носят весьма сложный характер, т.к. эл. машины во первых не однородна по материалу, во вторых имеет рассредоточенные внутренние источники тепла, интенсивность которых зависит от режима, скорости и т.д. Поэтому для дальнейшего анализа тепловых переходных процессах в ЭП, применим следующие допущения:
и при некоторой температуре двигателя наступает установившийся режим, после чего всё выделяемое при работе тепло рассеивается в окружающую среду., а температура двигателя при условии неизменности нагрузки на его валу в дальнейшем не меняется. Необходимо отметить, что реальные термодинамические процессы в ЭП носят весьма сложный характер, т.к. эл. машины во первых не однородна по материалу, во вторых имеет рассредоточенные внутренние источники тепла, интенсивность которых зависит от режима, скорости и т.д. Поэтому для дальнейшего анализа тепловых переходных процессах в ЭП, применим следующие допущения: и с одинаковой температурой по всём точном объема тела.
и с одинаковой температурой по всём точном объема тела. (102)
(102) - теплоотдача
- теплоотдача - температура двигателя в градусах
- температура двигателя в градусах - температура окружающей среды
- температура окружающей среды
 - превышение температуры
- превышение температуры 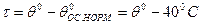
 (103)
(103) -потери мощности в двигателе
-потери мощности в двигателе -изменение превышения температуры
-изменение превышения температуры все члены уравнения 103 на
все члены уравнения 103 на  , то
, то (104)
(104)
 (сек) обозначим
(сек) обозначим  - постоянна времени нагрева, то с учётом этого уравнение (104) будет иметь вид:
- постоянна времени нагрева, то с учётом этого уравнение (104) будет иметь вид: (105)
(105) до
до  . Решение этого уравнения имеет вид:
. Решение этого уравнения имеет вид:
 текущее время (с).
текущее время (с).
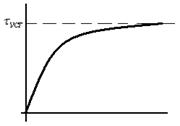
 , а затем выключить из питающей сети, то процесс его охлаждения до температуры окружающей среды может быть представлен в виде уравнения которое носит название решение уравнения теплового баланса при охлаждении и имеет следующий вид:
, а затем выключить из питающей сети, то процесс его охлаждения до температуры окружающей среды может быть представлен в виде уравнения которое носит название решение уравнения теплового баланса при охлаждении и имеет следующий вид: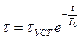 (106)
(106) - постоянная времени охлаждения она имеет такой же физический смысл что и постоянная времени нагрева, но в силу того, что в термодинамике процессы охлаждения имеют несколько большую инерционность, чем процессы нагрева для одного и того же двигателя, находятся примерно в таком соотношении:
- постоянная времени охлаждения она имеет такой же физический смысл что и постоянная времени нагрева, но в силу того, что в термодинамике процессы охлаждения имеют несколько большую инерционность, чем процессы нагрева для одного и того же двигателя, находятся примерно в таком соотношении:
 , то
, то (107)
(107)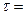

 получим, что
получим, что  .
. (108)
(108) , тогда:
, тогда: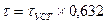
 .
.

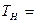 1-й степени габаритов двигателя и определение номинальной мощности двигателя малой мощности (до 100кВт) открытого исполнения постоянной времени нагрева находиться в пределах 1 минуты
1-й степени габаритов двигателя и определение номинальной мощности двигателя малой мощности (до 100кВт) открытого исполнения постоянной времени нагрева находиться в пределах 1 минуты  при
при  имеет следующий вид:
имеет следующий вид:
 зависит от нагрузки на валу двигателя (
зависит от нагрузки на валу двигателя ( - механической мощности), чем больше нагрузка, тем двигатель нагревается быстрее. Однако при этом будет изменяться величина установившейся температуры. Зависимость
- механической мощности), чем больше нагрузка, тем двигатель нагревается быстрее. Однако при этом будет изменяться величина установившейся температуры. Зависимость 




