
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представление 2-х массовой системы в переменных состояниях.Содержание книги
Поиск на нашем сайте
На ряду с представленной моделью в переменных «входы-выходы» в которой используются передаточной функции отдельных звеньев и построенные из них структурные схемы, в настоящее время их используют для моделирования сложных систем, так называемый метод «пространство-состояний».
входные выходные переменные состояния
Рис.8.
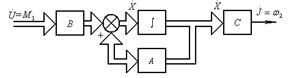
При этом структурная схема имеет следующий вид:
Рис.9.
матрица коэффициентом перед членами уравнений связи между входными и выходными величинами. Для 2-х массовой механической системы этот метод будет иметь следующее решение:
Уравнение
(10)
Рис.10.
Представить динамические модели в переменных состояниях для постановки задачи
Одномассовая механическая модель силового канала ЭП.
Тогда:
Рис.11.
Тогда система уравнений описывающая 2-х массовую механическую модель сведётся к одному уравнению:
В этом уравнении левая часть может быть графически представлена в виде 2-х функций
При анализе механической части с помощью этого уравнения возникает проблема связанная с недостатком каталожных данных о суммарном моменте инерции вращающихся частей, поэтому зачастую используют уравнение (11) записываемые в так называемых инженерных координатах.
Рис.12.
В этом уравнении:
Если представить:
Уравнения записываемые в виде (11) – уравнение движения в классических координатах (классическое, основное). (13) – уравнение движения в инженерных координатах. В уравнении (13)
Одномассовая механическая модель как объект управления (аналоговый вариант).
|
|||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.247.170 (0.01 с.) |

 В математическом описании метода, присутствуют не только входные воздействия и выходные переменные, а также внутренние промежуточные переменные, число которых равно числу дифференциальных уравнений входящих в систему и которые называются переменными состояниями. Все эти переменные образуют следующую структуру:
В математическом описании метода, присутствуют не только входные воздействия и выходные переменные, а также внутренние промежуточные переменные, число которых равно числу дифференциальных уравнений входящих в систему и которые называются переменными состояниями. Все эти переменные образуют следующую структуру:





 В общем виде решения задачи для существующих сколь угодно сложной системы в переменной состоянии сводиться к системе 2-х уравнений:
В общем виде решения задачи для существующих сколь угодно сложной системы в переменной состоянии сводиться к системе 2-х уравнений:
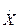 - вектор состояния системы.
- вектор состояния системы. - число уравнений.
- число уравнений.
 - соответственно для каждого из уравнений переменная выраженная в каждом из уравнений в качестве входных
- соответственно для каждого из уравнений переменная выраженная в каждом из уравнений в качестве входных - вектор входных переменных
- вектор входных переменных - число входных переменных
- число входных переменных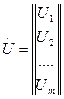
 -вектор выходных переменных
-вектор выходных переменных - число выходных переменных
- число выходных переменных

 - матрица промежуточных переменных или параметрическая матрица которая представляет из себя матрицу коэффициентов при переменных состояния.
- матрица промежуточных переменных или параметрическая матрица которая представляет из себя матрицу коэффициентов при переменных состояния.
 - строки -
- строки -  - входная матрица системы представляет из себя матрицу коэффициентов перед входными переменными.
- входная матрица системы представляет из себя матрицу коэффициентов перед входными переменными.
 - выходная матрица системы – параметрическая матрица.
- выходная матрица системы – параметрическая матрица.
 - проходная матрица
- проходная матрица
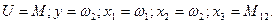
 относительно производных:
относительно производных: (7)
(7) (8)
(8) (9)
(9)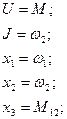







 Если считать, что жесткость механической связи между 2-мя вращающимися массами равна бесконечности, то можно считать 2-х массовую механическую модель адекватной 1-о массовой.
Если считать, что жесткость механической связи между 2-мя вращающимися массами равна бесконечности, то можно считать 2-х массовую механическую модель адекватной 1-о массовой.

 (11)
(11) и
и  , при этом если строго следовать физическому смыслу этих функций, то
, при этом если строго следовать физическому смыслу этих функций, то  В этом случае нахождение точки статического равновесия, а именно равенства
В этом случае нахождение точки статического равновесия, а именно равенства  окажется невозможным. Поэтому обе характеристики для удобства анализа располагает в одном квадранте, чаще во 2-м. Тогда уравнение (11) будет иметь вид арифметического уравнения.
окажется невозможным. Поэтому обе характеристики для удобства анализа располагает в одном квадранте, чаще во 2-м. Тогда уравнение (11) будет иметь вид арифметического уравнения. момент инерции выражается через произведение массы на квадрант приведенного радиуса инерции, которое достаточно легко определиться при наличии данных о габаритах и массе вращающихся частей, тогда уравнение примет вид:
момент инерции выражается через произведение массы на квадрант приведенного радиуса инерции, которое достаточно легко определиться при наличии данных о габаритах и массе вращающихся частей, тогда уравнение примет вид: (12)
(12) , где
, где  , то уравнение примет вид:
, то уравнение примет вид: (13)
(13)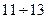 являются математическим описанием 1-о массовой механической моделью и называе6тся соответственно:
являются математическим описанием 1-о массовой механической моделью и называе6тся соответственно: принято называть маховый момент.
принято называть маховый момент.


