
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ЭП в переменных «ВХОДА-ВЫХОДА»Содержание книги
Поиск на нашем сайте
Математическое описание Синхронной машины, необходимое для создания простой и удобной динамической модели должно включать в себя: 1. уравнение зависимости синхронного момента синхронной машины от нагрузки. 2. уравнение зависимости асинхронного момента синхронной машины от динамической жесткости. 3. математическая модель синхронного ЭП кроме перечисленных 2-х уравнений должна содержать также классическое уравнение движения ЭП:
Момент созданный 3-х фазной обмоткой статора коммутации и ОВ. Если иметь в виду что область номинальных нагрузок (моментов) соответствует
Известно, что
Кроме того, известно, что ротор синхронной машины снабжён дополнительной обмоткой типа «беличье колесо», которая обеспечивает дополнительную составляющую момента (асинхронную), которую можно представить как:
где
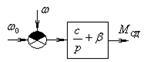
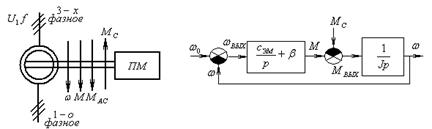
Рис. 72 - Структурная схема динамической модели синхронного электродвигателя
Динамическая модель синхронного электропривода кроме 2-ух уравнений (78-79) будет включать в себя уравнение (80):
Рис.73 - Структурная схема динамической модели синхронного ЭП.
Переходные процессы в ЭП возникают при регулировании угловой скорости вращения пуске, торможение, изменении нагрузки на валу ЭД
Одновременно с изменением угловой скорости изменяют моменты, действующее в ЭП и температура двигателя 1-анализ электромеханических переходных процессов. 2- анализ тепловых переходных процессов.
Электромеханические переходные Процессы и их анализ. Математическим описанием динамического процесса в ЭП является известное классическое уравнение движения:
где Практически любой процесс в ЭП можно считать динамическим, а статический режим, при Они имеют вид: 1. 2. 3. 4. 3 и 4 характеристики зачастую называют нагрузочными диаграммами ЭП. Кроме того при анализе используют так же динамические характеристики: 5. 6. Прежде, чем построить эти характеристики необходимо решить задачу по определению длительности переходного процесса. Такие задачи решают путём анализа уравнения (83), который заключается в решении этого уравнения относительно
В зависимости от характера изменения моментов в этом уравнении интегрирования может быть линейным,либо нелинейным. Различают следующие разновидности этой задачи: 1. 2. 3. а) б)
Решение уравнения движения при постоянном В общем, виде эта задача решается при
Частный случай: при определении
где Как правило такие задачи решаются наиболее часто. Иногда по технологическому процессу необходимо знать также а) самоторможение. б) электрическое торможение.
а) Двигатель останавливается посредством отключения его от источника питания
При определении времени электрического необходимо учитывать величину тормозного электромагнитного момента, направление которого совпадает с
Обычно такие задачи являются идеализированными и как правило, используются для проведения предварительных расчётов.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.006 с.) |

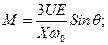 (73)
(73) находящихся в пределе
находящихся в пределе 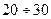 и в этой области зависимости
и в этой области зависимости 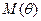 носит практически линейный характер, то:
носит практически линейный характер, то: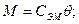 (74)
(74) может быть физически представлен в виде жесткости упругой электромагнитной связи, которая в этом случае будет аналогична жесткости упругой связи в механической модели ЭП (см. гл «Динамические модели 2-х массовой механической системы»). При этом растяжение упругой электромагнитной связи между осями в магнитном поле и ротора, равное углу
может быть физически представлен в виде жесткости упругой электромагнитной связи, которая в этом случае будет аналогична жесткости упругой связи в механической модели ЭП (см. гл «Динамические модели 2-х массовой механической системы»). При этом растяжение упругой электромагнитной связи между осями в магнитном поле и ротора, равное углу 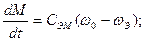 (75)
(75)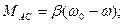 (76)
(76)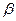 - динамическая жесткость
- динамическая жесткость 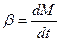 (см. «динамическая модель 2-х массовой машины»)
(см. «динамическая модель 2-х массовой машины»)  Синхронный двигатель может быть представлен в виде следующей структурной схемы с учётом выбора переменных:
Синхронный двигатель может быть представлен в виде следующей структурной схемы с учётом выбора переменных: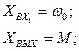
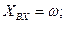
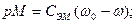 (77)
(77)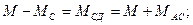 (79)
(79)
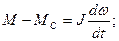 (80)
(80)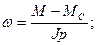 (81)
(81)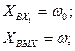
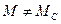
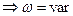 (изменяется угловая скорость вращения). Динамический процесс может быть представлен в виде классического уравнения двигателя ЭП.
(изменяется угловая скорость вращения). Динамический процесс может быть представлен в виде классического уравнения двигателя ЭП. , (83)
, (83)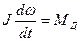 - избыточный динамический момент.
- избыточный динамический момент.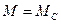 ;
; 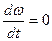 ;
; 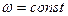 -т частный случай динамических процессов. Обычно в качестве конечной задачей по анализу переходных процессов в ЭП является расчёт и построение так называемых динамических характеристик ЭП.
-т частный случай динамических процессов. Обычно в качестве конечной задачей по анализу переходных процессов в ЭП является расчёт и построение так называемых динамических характеристик ЭП.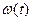 - график движения (кривая движения) частные случаи этой характеристики - кривая разгона (пуска); кривая торможения.
- график движения (кривая движения) частные случаи этой характеристики - кривая разгона (пуска); кривая торможения.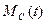 - характеризует характер изменения статического момента сопротивления механизма во времени.
- характеризует характер изменения статического момента сопротивления механизма во времени. - характер изменения электромагнитного момента во времени.
- характер изменения электромагнитного момента во времени.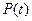 - характеризует изменения механической мощности на валу двигателем во времени.
- характеризует изменения механической мощности на валу двигателем во времени.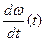 -характер изменения угловой скорости во времени.
-характер изменения угловой скорости во времени.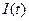 - характер изменения тока, потребляемого двигателя во времени.
- характер изменения тока, потребляемого двигателя во времени. :
: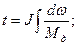
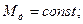
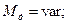 (линейно изменяется).
(линейно изменяется).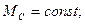
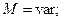
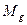 .
.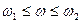 .
.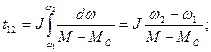 (84)
(84)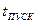 при
при 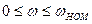 .
.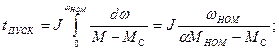
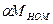 - среднее значение электромагнитного момента за время пуска.
- среднее значение электромагнитного момента за время пуска.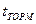 анализируется 2 варианта:
анализируется 2 варианта: )двигатель останавливается под действием
)двигатель останавливается под действием  .
.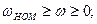
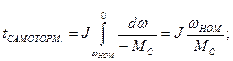 (85)
(85)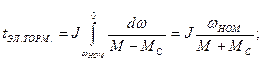 (85)
(85)


