
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое описание обобщенной асинхронной машины.Содержание книги
Поиск на нашем сайте
Обобщенная асинхронная машина показана на рис 59. Она содержит трехфазную обмотку на статоре и трехфазную обмотку на роторе. Обмотки статора и ротора подключены к симметричным трехфазным источникам напряжения. Математическое описание такой машины базируется на известных законах. Уравнением равновесия э.д.с. на обмотках статора и ротора базируются на втором законе Кирхгофа.
Рис.59 – Обобщенная асинхронная машина
Для статора: Для ротора:
(48)
В уравнениях (481) фигурируют мгновенные напряжения, токи потокосцепления статора и ротора, а также активное сопротивление обмоток. Обычно обмотки выполняются симметричными, и поэтому Вторым используемым законом является закон Ампера, который связывает потокосцепление обмоток с токами, протекающими по обмоткам:
(48*)
Для ротора:
Удивительно симметричные уравнения для определения потокосцеплений показывают, что потокосцепление каждой обмотки зависит от токов во всех обмотках; эти зависимости проявляются через взаимоиндукцию. В уравнениях (48*) Третьим законом, лежащим в основе анализа, является второй закон Ньютона – закон равновесия моментов на валу машины:
где
Наконец, четверым и последним законом, лежащим в основе анализа машины, является закон, сформулированный Ленцем как правило левой руки. Этот закон связывается векторные величины момента, потокосцепления и тока:
Следует сразу подчеркнуть, что, несмотря на полное и строгое математическое описание, использование уравнений (48) – (50) для исследование машины встречает серьезные трудности. В уравнениях (49 и 50) фигурируют векторные величины, а в уравнениях (48 и 48*) скалярные;
Количество взаимосвязанных уравнений равно 14, а количество коэффициентов – 4; Коэффициенты взаимоиндуктивности между обмотками статора и ротора в уравнениях (48*) является нелинейным, так как в нем перемножаются переменные. На пути упрощения математического описания асинхронной машины, да и вообще всех машин переменного ток, удивительно удачным и изящным оказался метод пространственного вектора, который позволит существенно упростить и сократить вышеприведенную систему уравнений; метод позволяет связать уравнения (48 -50) в единую систему с векторными переменными состояния. Суть метод состоит в том, что мгновенные значения симметричным трехфазных переменных состояния (напряжения, токи, потоскостцепления0 можно математически преобразовать так, чтобы они были представлены одним пространственным вектором. это математическое преобразование имеет вид (например, для тока статора):
где
На рисунке 60 представлена геометрическая интерпретация пространственного вектора тока – это вектор на комплексной плоскости с модулем (длиной) Теперь можно переходить к упрощению уравнении. Рисунок 60– Пространственный вектор тока.
Шаг первый. Для преобразования уравнений (48) в мгновенных значениях к уравнениям в пространственных векторах умножим их на выражения, (первый уравнения на
(52) где
Таким образом, вместо двенадцати уравнений (48) – (48*) получено лишь четыре уравнения(52). Шаг второй. Переменные коэффициенты взаимной индуктивности у уравнениях для потокосцеплений (52) являются результатом того, что уравнения равновесия э.д.с. для статора записаны в неподвижной системе координат, связанной со статором, а уравнения равновесия э.д.с. для ротора записаны во вращающейся системе координат, связанной с ротором. Метод пространственного вектора позволяет записать эти уравнения в единой системе координат, вращающейся с произвольной скоростью
(53)
где В уравнениях (53) все коэффициен6ты являются величинам постоянным, имеют четкий физический смысл и могут быть определены по паспортным данным двигателя, либо экспериментально. Шаг третий. Этот шаг связан с определением момента. момент в уравнении (50) является векторным произведением любой пары векторов. Из уравнения (53) следует, что таких пар может быть шесть
Шаг четвертый. На этом этапе уравнения (49), (53) и (54) приводят к безразмерным (относительным) величинам. В качестве основных базовых величин набираются амплитудные номинальные значения фазного напряжения и тока, а также номинальные значения угловой частоты:
На этой основе определяются базовые значения всех переменных и коэффициентов, входящих в уравнение, а также базового времени:
(56)
В этих уравнениях все переменные относительные, полученные как результат деления реальных значений на базовые, все коэффициенты также безразмерные, полученные аналогично. Переменные и параметры в относительных единицах:
В уравнениях (55) время принято безразмерные
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.25.216 (0.01 с.) |




 - активное сопротивление статорной обмотки,
- активное сопротивление статорной обмотки,  - активное сопротивление роторной обмотки.
- активное сопротивление роторной обмотки. Для статора:
Для статора:
 являются собственными индуктивностями соответствующих обмоток, все остальные – взаимоиндуктивностями между соответствующими обмотками.
являются собственными индуктивностями соответствующих обмоток, все остальные – взаимоиндуктивностями между соответствующими обмотками. (49)
(49) (кГМ2)- момент инерции на валу машины, учитывающий инерционность как самой машины, так и приведенной к валу инерционности рабочего механизма и редуктора;
(кГМ2)- момент инерции на валу машины, учитывающий инерционность как самой машины, так и приведенной к валу инерционности рабочего механизма и редуктора;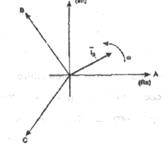
 (
( ) – угловая скорость вала машины;
) – угловая скорость вала машины; (Нм) – момент рабочего механизма, приведенный к валу, в общем случае он может быть функцией скорости и угла поворота.
(Нм) – момент рабочего механизма, приведенный к валу, в общем случае он может быть функцией скорости и угла поворота. (50)
(50) (51)
(51)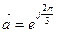 ,
,  - векторы, учитывающие пространственное смещение обмоток;
- векторы, учитывающие пространственное смещение обмоток; - Трехфазная симметричная токов статора. подставим в уравнения (51) значение мгновенных токов, найдем математическое описание пространственного вектора статора ока:
- Трехфазная симметричная токов статора. подставим в уравнения (51) значение мгновенных токов, найдем математическое описание пространственного вектора статора ока: (51*)
(51*)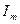 , вращающийся с угловой скоростью
, вращающийся с угловой скоростью 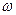 в положительном направлении. Проекции вектора
в положительном направлении. Проекции вектора  на фазные оси А, В, С определяют мгновенные токи в фазах. Аналогично пространственными векторами можно представить все напряжения, токи и потокосцепление, входящие в уравнения (48), (48*).
на фазные оси А, В, С определяют мгновенные токи в фазах. Аналогично пространственными векторами можно представить все напряжения, токи и потокосцепление, входящие в уравнения (48), (48*).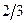 , вторые – на
, вторые – на  , третьи – на
, третьи – на 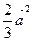 )и сложим раздельно для статора и ротора. Тогда получим:
)и сложим раздельно для статора и ротора. Тогда получим:
 - собственные индуктивности статора и ротора;
- собственные индуктивности статора и ротора; - взаимная индуктивность между статором и ротором.
- взаимная индуктивность между статором и ротором.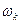 . В этом случае уравнения (52) преобразуются к виду:
. В этом случае уравнения (52) преобразуются к виду: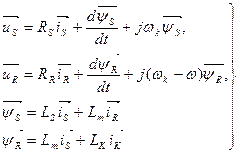
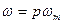 ,
,  - число пар полюсов в машине.
- число пар полюсов в машине. ;
;  ;
;  ;
;  ;
;  ;
;  . Часто в рассмотрение вводиться потокосцепление взаимной индукции
. Часто в рассмотрение вводиться потокосцепление взаимной индукции  . В том случае появляется ещё четыре возможности представления электромагнитного момента машины через следующие пары:
. В том случае появляется ещё четыре возможности представления электромагнитного момента машины через следующие пары:  ;
;  ;
;  ;
;  . После выбора той или иной пары уравнение момента приобретает определённости, а количество уравнений в системе (53) сокращается до двух. Кроме того, в уравнениях (49) и (50) векторные величины момента и скорости могут быть заменены их модульными значениями. Это является следствием того, что пространственные векторы токов и потокосцепления расположены в плоскости, перпендикулярной оси вращения, а векторы момента и угловой скорости совпадают с осью. В качестве примера покажем запись уравнений момента через некоторые пары переменных состояния машины.
. После выбора той или иной пары уравнение момента приобретает определённости, а количество уравнений в системе (53) сокращается до двух. Кроме того, в уравнениях (49) и (50) векторные величины момента и скорости могут быть заменены их модульными значениями. Это является следствием того, что пространственные векторы токов и потокосцепления расположены в плоскости, перпендикулярной оси вращения, а векторы момента и угловой скорости совпадают с осью. В качестве примера покажем запись уравнений момента через некоторые пары переменных состояния машины. (54)
(54) ,
,  ,
,  , (55)
, (55)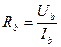 ,
,  ,
,  ,
,  ,
,  . (55*)
. (55*) В дальнейшем используются только в относительных величинах. Обобщенная система уравнений для описания асинхронной машины принимает вид:
В дальнейшем используются только в относительных величинах. Обобщенная система уравнений для описания асинхронной машины принимает вид: ,
,  ,
,  - относительные электромагнитные переменные состояния;
- относительные электромагнитные переменные состояния; ,
,  - относительная частота статора и относительная скорость ротора;
- относительная частота статора и относительная скорость ротора; - относительный момент на валу машины;
- относительный момент на валу машины; ,
,  ,
,  ,
, 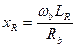 ,
,  ,
,  - относительные параметры.
- относительные параметры. , то есть единицей измерения времени является не секунда, а
, то есть единицей измерения времени является не секунда, а  . Следует заметить, что введение относительных величин сокращает время моделирования и позволяет устранить многие проблемы моделирования. Рассмотрим предварительно вопросы преобразования координат, а затем модели асинхронной машины в различных системах координат и их основные характеристики.
. Следует заметить, что введение относительных величин сокращает время моделирования и позволяет устранить многие проблемы моделирования. Рассмотрим предварительно вопросы преобразования координат, а затем модели асинхронной машины в различных системах координат и их основные характеристики.


