
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каноническое уравнение прямойСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
8 Уравнение пучка прямых с центром в точке А(x1, y1) имеет вид: y-y1 = (x-x1), где - параметр пучка. Если пучок задается двумя пересекающимися прямыми A1 x + B1 y + C1= 0, A2 x + B2 y + C2 = 0, то его уравнение имеет вид: (A1 x + B1 y + C1) + (A2 x + B2 y + C2)=0, где и - параметры пучка, не обращающиеся в 0 одновременно. Величина угла между прямыми y = kx + b и y = k1 x + b1 задается формулой: tg = Равенство 1 + k1 k = 0 есть необходимое и достаточное условие перпендикулярности прямых. Параллельные прямые Для того, чтобы два уравнения A1 x + B1 y + C1= 0, (7) A2 x + B2 y + C2 = 0, (8) задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны: A1/A2 = B1/B2 = C1/C2. Уравнения (2.7), (2.8) задают две различные параллельные прямые, если A1/A2 = B1/B2 и B1/B2 C1/C2; прямые пересекаются, если A1/A2 не = B1/B2. Расстояние от точки до прямой
Расстояние d от точки Mо(xо, yо) до прямой есть длина перпендикуляра, проведенного из точки Mо к прямой. Если прямая задана нормальным уравнением, то d = rо nо - р , где rо - радиус-вектор точки Mо или, в координатной форме, d = xо cos + yо sin - р . Угол между двумя прямыми
Необходимое и достаточное условие перпендикулярности двух прямых
Расстояние между параллельными прямыми Если прямые заданы уравнениями
а если уравнениями
8. Прямая линия в пространстве. Способы задания Прямая в пространстве может быть задана: 1) как линия пересечения двух плоскостей, т.е. системой уравнений: A1 x + B1 y + C1 z + D1 = 0, A2 x + B2 y + C2 z + D2 = 0; (2) 2) двумя своими точками M1(x1, y1, z1) и M2(x2, y2, z2), тогда прямая, через них проходящая, задается уравнениями: 3) точкой M1(x1, y1, z1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями: Уравнения (4) называются каноническими уравнениями прямой. Вектор a называется направляющим вектором прямой. Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: x = x1 +mt, y = y1 + nt, z = z1 + рt. (5) Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой: x = mz + a, y = nz + b. (6) От уравнений (6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения: От общих уравнений (2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор n = [n1, n2], где n1(A1, B1, C1) и n2(A2, B2, C2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система равносильна системе Система На практике можно пользоваться готовой формулой: если прямая задана пересечением двух плоскостей
9. Плоскость, способы её задания Всякое уравнение первой степени относительно координат x, y, z Ax + By + Cz +D = 0 (1) задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (1), которое называется уравнением плоскости. Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (1) коэффициенты A, B, C одновременно не равны 0. Особые случаи уравнения (1): 1) By + Cz + D = 0 - параллельна оси Ox; 2) Ax + Cz + D = 0 - параллельна оси Oy; 3) Ax + By + D = 0 - параллельна оси Oz; 4) Cz + D = 0 - параллельна оси Oxy; 5) By + D = 0 - параллельна оси Oxz; 6) Ax + D = 0 - параллельна оси Oyz; 7) Ax + By + Cz = 0 - проходит через начало координат; 8) By + Cz = 0 - проходит через ось Ox; 9) Ax + Cz = 0 - проходит через ось Oy; 10) Ax + By = 0 - проходит через ось Oz; 11) z = 0 - плоскость Oxy; 12) y = 0 - плоскость Oxz; 13) x = 0 - плоскость Oyz. Уравнения координатных плоскостей: x = 0, y = 0, z = 0. Уравнение плоскости в отрезках где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.
где Приведение общего уравнения плоскости к нормальному виду:
Здесь Уравнение плоскости по точке и нормальному вектору В векторном виде В координатах
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 478; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.181 (0.006 с.) |


 .
.


 или
или  или
или 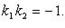
 и
и  то
то
 и
и  то
то 
 =
=  ; (3)
; (3) . (4)
. (4) .
.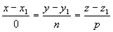
 ; такая прямая перпендикулярна к оси Ох.
; такая прямая перпендикулярна к оси Ох. равносильна системе x = x1, y = y1; прямая параллельна оси Oz.
равносильна системе x = x1, y = y1; прямая параллельна оси Oz. , то вектор
, то вектор  является направляющим вектором данной прямой.
является направляющим вектором данной прямой.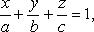

 - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.
- углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.
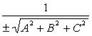 - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если
- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если  произвольно, если D = 0.
произвольно, если D = 0.




