
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нормальное уравнение прямой.Содержание книги
Поиск на нашем сайте
Рассмотрим произвольную прямую. Проведем из начала координат перпендикуляр к данной прямой. Пусть Р – основание перпендикуляра (см. рис. 3.3). Вектор x cos a + y sin a – p = 0. (3.9)
Рис. 3.3
Заметим, что р не может быть отрицательным, так как это расстояние от точки О до прямой. Пусть М¢ (х¢, у¢) – произвольная точка плоскости. Выражение Укажем алгоритм приведения общего уравнения прямой (3.1) к нормальному виду (3.9): для этого надо умножить всё уравнение Ах + Ву + +С = 0 на нормирующий множитель Обозначим d – расстояние от точки М¢ (х¢, у¢) до данной прямой. Используя нормирующий множитель, можно получить формулу для нахождения расстояния от точки М¢ (х¢, у¢) до прямой, заданной общим уравнением:
5. Условия параллельности и перпендикулярности прямых. Пусть две прямые заданы общими уравнениями: Условие параллельности этих прямых эквивалентно условию коллинеарности (2.8) векторов нормалей к этим прямым
Условие перпендикулярности этих прямых эквивалентно равенству нулю скалярного произведения (2.11) векторов нормалей
Угол между прямыми равен углу между нормалями к этим прямым, который определяется по формуле
Абсолютно аналогично обстоит дело, если прямые заданы каноническими уравнениями: Условие параллельности, перпендикулярности, а также угол между прямыми можно определить, используя направляющие векторы прямых Условие параллельности:
Условие перпендикулярности:
Угол между прямыми: Пусть теперь прямые заданы уравнениями с угловыми коэффициентами: Условие параллельности прямых:
Угол между прямыми находится по формуле:
Условие перпендикулярности прямых: Пример. Написать уравнение прямой, проходящей через точку М (1, –2) и составляющей угол в 45° с прямой у = 2 х + 5. Решение. Ясно, что такую прямую можно провести двумя способами (рис. 3.4):
Рис. 3.4
Воспользуемся формулой (3.18), причем имеем tga = 1,
Решая эти уравнения, получаем два разных значения углового коэффициента искомой прямой: Воспользуемся теперь уравнением (3.8) прямой с угловым коэффициентом и проходящей через заданную точку. Получим два варианта искомой прямой:
Окончательно получаем
Виды уравнений плоскости
Определение 3.2. Уравнение вида Ах + Ву + Сz + D = 0, где А, В, C и D – некоторые числа, называется уравнением первой степени. Теорема 3.1. В декартовой системе координат любое уравнение первой степени определяет некоторую плоскость и, наоборот, любая плоскость в декартовой системе координат определяется уравнением первой степени. Рассмотрим различные виды уравнений плоскости. Общее уравнение плоскости. Уравнение вида Ах + Ву + Сz + D = 0 (3.20) называется общим уравнением плоскости. Геометрический смысл коэффициентов А, В и С в уравнении (3.20): они являются координатами вектора нормали n к этой плоскости, т.е. вектора, перпендикулярного данной плоскости.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.154.133 (0.008 с.) |

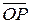 является вектором нормали к данной прямой. Если a – угол наклона вектора
является вектором нормали к данной прямой. Если a – угол наклона вектора 
 называется отклонением точки М¢ от данной прямой. По знаку отклонения d (M¢) можно определить взаимное расположение точек М¢ и О относительно прямой: если d (M¢) > 0, то М¢ и О лежат по разные стороны от прямой; если d (M¢) < 0, то М¢ и О лежат по одну сторону от прямой.
называется отклонением точки М¢ от данной прямой. По знаку отклонения d (M¢) можно определить взаимное расположение точек М¢ и О относительно прямой: если d (M¢) > 0, то М¢ и О лежат по разные стороны от прямой; если d (M¢) < 0, то М¢ и О лежат по одну сторону от прямой. , знак которого противоположен знаку свободного коэффициента.
, знак которого противоположен знаку свободного коэффициента. (3.10)
(3.10) и
и  .
. и
и  , т.е.
, т.е. (3.11)
(3.11) или
или (3.12)
(3.12) (3.13)
(3.13) .
. и
и  .
.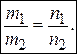 (3.14)
(3.14) (3.15)
(3.15) (3.16)
(3.16) .
. (3.17)
(3.17) (3.18)
(3.18) (3.19)
(3.19)
 . Тогда
. Тогда  . Это уравнение эквивалентно двум уравнениям:
. Это уравнение эквивалентно двум уравнениям: или
или  .
. или
или  .
. или
или  .
. или
или  .
.


