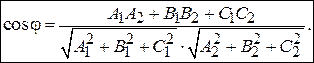Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметрические уравнения прямой.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим канонические уравнения (3.29) прямой и примем за параметр t каждое из данных отношений:
Эти уравнения являются параметрическими уравнениями прямой. Примеры. Написать уравнения прямой, проходящей через точку Решение. Направляющим вектором этой прямой служит нормальный вектор плоскости a: п = (2, –3, 1). Воспользуемся каноническими уравнениями (3.29), тогда уравнения искомой прямой примут вид:
5. Взаимное расположение прямых и плоскостей в пространстве 1). Пусть в пространстве заданы плоскость a и прямая L:
Условие параллельности прямой L и плоскости a эквивалентно условию перпендикулярности нормали п = (А, В, С) плоскости a и направляющего вектора а = (l, m, n) прямой L и выражается равенством нулю скалярного произведения (2.11) векторов п и а, т.е. Al + Bm + Cn = 0. (3.32) Условие перпендикулярности прямой L и плоскости a эквивалентно условию коллинеарности (2.8) векторов п и а, т.е.
Как легко убедиться, условие принадлежности прямой L к плоскости a выражается двумя равенствами:
Угол j между прямой L и плоскостью a находится по формуле
2). Пусть в пространстве заданы две прямые своими каноническими уравнениями:
Условия параллельности, перпендикулярности Условие параллельности: Условие перпендикулярности: Угол между прямыми: 3). Пусть в пространстве заданы две плоскости
Условия параллельности, перпендикулярности Условие параллельности:
Условие перпендикулярности:
Угол между плоскостями: (3.41)
Контрольные вопросы 1. Общее уравнение прямой, неполные уравнения прямой, уравнение прямой в отрезках. 2. Каноническое уравнение прямой, уравнение прямой, проходящей через две заданные точки, уравнение прямой, проходящей через заданную точку, перпендикулярно заданному вектору. 3. Параметрические уравнения прямой, уравнение прямой с угловым коэффициентом, нормальное уравнение прямой. 4. Расстояние от точки до прямой. 5. Условия параллельности и перпендикулярности прямых, заданных общими уравнениями. Нахождение угла между этими прямыми. 6. Условия параллельности и перпендикулярности прямых, заданных в виде с угловым коэффициентом. Нахождение угла между этими прямыми. 7. Общее уравнение плоскости, неполные уравнения плоскости, уравнение плоскости в отрезках. 8. Уравнение плоскости, проходящей через три точки, Уравнение плоскости, параллельной заданному вектору и проходящей через две заданные точки, уравнение плоскости, параллельной двум неколлинеарным векторам и проходящей через заданную точку. 9. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору. Нормальное уравнение плоскости. Расстояние от точки до плоскости. 10. Общие, канонические и канонические уравнения прямой в пространстве. Уравнения прямой, проходящей через две заданные точки. 11. Условия параллельности и перпендикулярности прямой и плоскости. Вычисление угла между прямой и плоскостью. 12. Условия параллельности и перпендикулярности двух прямых. Вычисление угла между прямыми. 13. Условия параллельности и перпендикулярности двух плоскостей. Вычисление угла между плоскостями.
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 596; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.251.103 (0.007 с.) |

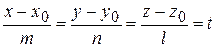 . Получим:
. Получим: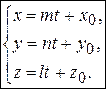 (3.31)
(3.31)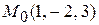 и перпендикулярно плоскости a: 2 х – 3 y + z – 1 = 0.
и перпендикулярно плоскости a: 2 х – 3 y + z – 1 = 0.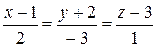 .
.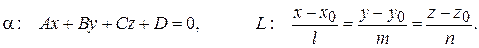
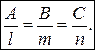 (3.33)
(3.33)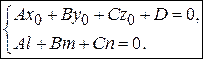 (3.34)
(3.34)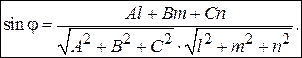 (3.35)
(3.35)
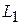 и
и 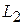 , а также угол между
, а также угол между  и
и 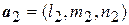 данных прямых.
данных прямых. (3.36)
(3.36)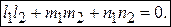 (3.37)
(3.37)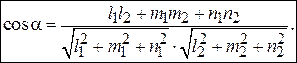 (3.38)
(3.38)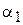 и
и 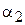 своими общими уравнениями:
своими общими уравнениями:
 и п
и п 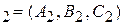 к плоскостям.
к плоскостям.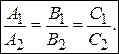 (3.39)
(3.39)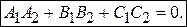 (3.40)
(3.40)