
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения масс в функции от главных размеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Входящие в уравнение (2.7) слагаемые можно выразить в зависимости от главных размерений судна, что позволяет, решив это уравнение непосредственно определять размерения как искомые величины. При этом можно рассматривать следующие три частных случая. 1. В исходных данных на проектирование задана мощность главных двигателей. С учетом уравнения масс и плавучести и используемых выше подстановок уравнение (2.7) запишем следующим образом LBTrd = Y к LBH + ( или после преобразования
Введем следующие обозначения соотношений главных размерений:
Тогда уравнение (2.14) после подставки в него главных размерений выраженных из этих соотношений, примет вид
откуда
Остальные главные размерения могут быть получены по известной ширине судна из условия сохранения геометрического подобия корпуса L = l B, T = b B, H = cT. По полученным главным размерениям далее может быть определено в первом приближении водоизмещение судна D = S Рi, или в развернутом виде
2. В исходных данных на проектирование наряду с мощностью главных двигателей задана осадка судна. В этом случае уравнение (2.14) можно записать
3. Если в исходных данных задана скорость хода судна, тогда мощность главных двигателей, входящая в уравнение (2.14) следует представить, используя формулу адмиралтейского коэффициента и уравнение масс и плавучести
Тогда уравнение масс в виде (2.15) преобразуется в кубическое уравнение
решением которого определяется ширина судна В. В случае если задана осадка судна и скорость его хода, тогда подставив в (2.16) выражение для мощности получим
Входящие в расчетные выражения относительные величины принимаются по судну-прототипу либо по соответствующим статистическим данным.
Уравнение масс в форме коэффициентов Утилизации водоизмещения
Различают два вида коэффициентов утилизации водоизмещения: - коэффициент утилизации водоизмещения по грузоподъемности
- коэффициент утилизации водоизмещения по дедвейту
Данные коэффициенты широко используются на различных стадиях создания судна в связи с тем, что они характеризуют его транспортный потенциал. Коэффициенты утилизации показывают долю полезной нагрузки (грузоподъемности или дедвейта) в полном водоизмещении судна. Например, судно грузоподъемностью Р гр=1000 т имеет полное водоизмещение D = 1400 т. Следовательно, коэффициент утилизации водоизмещения по грузоподъемности будет Наличие двух коэффициентов утилизации водоизмещения ставит вопрос об условиях применения каждого из них. Понятно, что если судно не грузовое (например, пассажирское, буксир и т.д.), то однозначно следует использовать коэффициент утилизации по дедвейту. Применительно к грузовым судам при выборе коэффициента следует руководствоваться следующими соображениями. При сопоставлении однотипных, близких по размерам, скоростям хода и автономности по запасам судов можно пользоваться коэффициентом утилизации водоизмещения по грузоподъемности. В противном случае, при различающихся скоростях хода и автономности по запасам – коэффициентом утилизации по дедвейту, поскольку сравнение судов в этом случае по h грбудет некорректным, так как при этом не будут учтены различия в ряде масс дедвейта. Учитывая, что грузовые суда внутреннего плавания близкой грузоподъемности, исходя из идентичных условий плавания, имеют и близкие значения скорости хода и автономности по запасам, то для них можно в таком случае рекомендовать использование коэффициента утилизации по грузоподъемности. Соответственно для грузовых судов смешанного (река-море) плавания и морских судов такой подход неприемлем. При анализе их весовой отдачи следует применять коэффициент утилизации водоизмещения по дедвейту. Другим направлением практического применения коэффициентов утилизации является их использование для оперативного определения водоизмещения судна при заданной его грузоподъемности или дедвейте
Насколько такой способ определения водоизмещения является простым, настолько же он является и приближенным. Приближенность эта связана с трудностью достоверного прогнозирования величины коэффициента утилизации. Обычно при подобных расчетах, величину коэффициента утилизации принимают по судну-прототипу. В табл. 2.1 приведены значения коэффициента утилизации водоизмещения по грузоподъемности для ряда типов грузовых судов.
Таблица 2.1 Коэффициент утилизации h гр для речных грузовых судов
Из табл. 2.1 видно, что величина коэффициента утилизации у грузовых судов колеблется в достаточно большем диапазоне и зависит, прежде всего, от грузоподъемности судна, конструктивного типа его корпуса, класса Регистра, скорости хода. Поскольку приведенные характеристики проектируемого судна и судна-прототипа часто отличаются, то возникает необходимость иметь способ количественного учета влияния данных характеристик на коэффициент утилизации водоизмещения. Запишем уравнение масс в следующем виде D = Р к + Р м + Р тс + Р гр + DD. Здесь принято допущение DW ° = Р гр, что для грузовых судов внутреннего плавания является приемлемым в силу небольших величин запасов по сравнению с грузоподъемностью судна. Сделав подстановки, аналогичные принятым в п.2.2, получим
При этом нужно иметь ввиду, что формула адмиралтейского коэффициента здесь использована в следующей модификации
Разделим уравнение (2.21) на водоизмещение D, а первое слагаемое справа умножим и разделим на или Сделаем подстановку х 2 = h гр, тогда получим
Решив данное квадратичное уравнение и сделав обратную подстановку h гр = х 2 для положительного значения корня будем иметь
Если пренебречь малыми членами этого выражения, имеющими вид
Полученное выражение иногда называют уравнением Поздюнина В.Л., который разработал способ определения водоизмещения с использованием коэффициента утилизации. Выражение для коэффициента утилизации по дедвейту получается аналогичным путем и имеет вид
Анализируя выражение (2.22) и (2.23) можно отметить, что увеличение грузоподъемности судна (дедвейта) ведет к увеличению коэффициента утилизации водоизмещения и, как отмечалось раньше, увеличивает долю полезной нагрузки в полной массе судна, его транспортный потенциал. Сказанное является одним из объяснений тому, что при наличии больших грузо- и пассажиропотоков используются суда большой грузоподъемности или пассажировместимости. Кстати отметим, что подобная закономерность «работает» и применительно к другим транспортным средствам и является одной из причин создания самолетов-аэробусов, большегрузных автомобилей и т.д. Увеличение скорости хода существенно снижает коэффициент утилизации водоизмещения, поскольку приводит пропорционально v3 к увеличению вычитаемого члена в анализируемых выражениях. Проектирование судна на более высокий класс (с большей высотой расчетной волны) приводит к увеличению доли массы корпуса в полном водоизмещении (измерителя а), что соответственно уменьшает коэффициент утилизации. Аналогичным образом по полученным выражениям можно проследить влияние на h гризменение характеристик энергетической установки
2.5. Дифференциальный способ Норманна определения Водоизмещения судна
Рассмотренные выше способы определения водоизмещения судна в конечном счете сводятся к решению той или иной системы нелинейных алгебраических уравнений. Точного результата при таком подходе можно получить лишь в некоторых специальных случаях. Точность решения можно существенно повысить, если его находить путем внесения малых изменений в проект уже построенного судна, которое может служить прототипом. Применительно к задаче определения водоизмещения судна это означает, что искомая величина D 1находится
где D – водоизмещение судна-прототипа; D 1 D – изменение (приращение) водоизмещения судна-прототипа, обусловленное его отличием от характеристик проектируемого судна. Задача нахождения главных неизвестных по данным судна-прототипа имеет вполне определенный математический смысл, и ее решение достигается на базе способа, который принято называть дифференциальным. В его основе лежит известная формула разложения непрерывной функции многих переменных в ряд Тейлора. Пусть имеется функция f (x, Y, …, t), значение которой при некоторых конкретных аргументах х = х о, у = у о … t = t оизвестно: f o = f (x o, y o, … t o ). Поставим задачу нахождения значения функции при новых аргументах х 1 = х о + Dх, у 1 = у о + Dу, … t 1 = t о + Dt, где D х, D у, D t – конечные приращения известных аргументов. Очевидно, что новое значение функции f 1 можно представить в следующем виде f 1 = f о + D f, где D f – приращение функции f, получающееся вследствие изменения (приращения) аргументов. Величину приращения функции D f можно найти, используя ряд Тейлора, если при значениях аргументов x o, y o, … t oизвестна не только сама функция f о, но и ее частные производные
здесь При условии, что приращения аргументов невелики, то без существенного ущерба для точности во многих технических задачах членом
Если вместо конечных приращений аргументов D х, Dу, D t подставить их дифференциалы, то полученное выражение оказывается полностью совпадающим с формулой полного дифференциала функции многих переменных, то есть
Отметим, что если вместо функции f (х, у,…t) рассматривать функцию
где Р – независимое слагаемое, то ее приращение можно записать D F = D P + D f» dP + d f. Учитывая конечность приращения независимого слагаемого (DР = dP) можно записать
Полученное выражение используется для определения приращения D 1 D в соответствии с которым принимают D 1 D = dD. После этих предварительных пояснений перейдем к изложению самого способа Нормана. Согласно выражения (2.24) при расчете по этому методу водоизмещения проектируемого судна задача сводится к определению приращения D 1 D. В этом случае уравнение масс имеет вид
Предположим, что в соответствии с заданием на проектирование нового судна ему требуется обеспечить иную по сравнению с прототипом скорость v = vо + D v, в связи со сменой типа главных двигателей изменяется измеритель масс механизмов
Полученное выражение содержит в качестве неизвестного приращение водоизмещения dD. Остальные же величины либо известны по заданию (d v, d Тогда искомая величина после простых преобразований будет равна
Данное выражение и носит название дифференциального уравнения масс Нормана. Если в (2.29) ввести обозначение для множителя и учесть при этом, что дифференциал (производная) от суммы равен сумме дифференциалов, то получим выражение для так называемого коэффициента Нормана
Дифференциальное уравнение масс Нормана (2.29) может быть истолковано следующим образом: выражения в скобках правой части формулы (2.27) есть приращение массы проектируемого судна по сравнению с прототипом (как сумма приращений отдельных его масс) вследствие изменения независимых переменных РН, v, dD = hН (dPH + SdPi). Уравнение (2.29) раскрывает механику парадокса теории проектирования: увеличение нагрузки существующего судна на величину DР увеличивает водоизмещение ровно на столько же, тогда как увеличение нагрузки на DР в задаче проектирования нового судна (обеспечение требуемых его характеристик) приводит к увеличению водоизмещения на dD = hН DР. Получим в качестве примера расчетные выражения для определения водоизмещения проектируемого судна методом Нормана т.е. в виде (2.24), приняв следующие зависимости составляющих массы судна (по уравнению (2.7) от его элементов и характеристик.
Согласно (2.27) найдем приращение водоизмещения судна-прототипа D1D как полный дифференциал от уравнения масс (2.7), который будет равен сумме частных дифференциалов от его членов, т.е.
Решая это уравнение относительно dD, получим
Множитель перед скобкой полученного выражения (2.32) есть коэффициент Нормана Конкретизируем вид данного выражения, для чего найдем значения входящих в него производных, используя при этом зависимости масс, принятые в (2.31).
и аналогично
Тогда выражение для коэффициента Нормана будет
или после умножения на D
Окончательно, учитывая значение разности масс выражения в знаменателе, получим
Полученное выражение при принятых условиях (2.31) можно использовать как расчетное для определения величины коэффициента hН. Кроме того, анализ этого выражения позволяет сделать некоторые выводы. Во-первых, коэффициент утилизации Нормана всегда положителен и больше единицы, поскольку числитель в (2.33) больше знаменателя. Во-вторых, если сравнивать два судна, имеющие приблизительно одинаковые величины водоизмещения, массы механизмов и топлива, то увидим, что численное значение коэффициента Нормана в этом случае будет зависеть от величины чистого дедвейта этих судов. А именно: чем больше чистый дедвейт судна, тем меньше коэффициент hН и наоборот. Как частный вывод из сказанного следует отметить, что если рассматривать грузовое и пассажирское судно близкого водоизмещения, то коэффициент Нормана пассажирского будет больше, чем у грузового. Это как раз и связано с тем, что дедвейт последнего больше, так как в его состав входит грузоподъемность судна. Данный вывод объясняет то обстоятельство, что у грузовых судов коэффициент hН в среднем имеет значение порядка 1,2¸1,5, тогда как у пассажирских он доходит до 2¸5. Выражение (2.32) можно привести к следующему виду
Здесь в скобках записана сумма приращений составляющих масс судна-прототипа при изменении тех или иных его характеристик, определяемая как полный дифференциал этих масс. Последний, в свою очередь, находится как сумма частных дифференциалов по соответствующим аргументам. В рассматриваемом примере
Найдем эти частные дифференциалы
Для массы запасов топлива и смазки аналогично будем иметь
Учитывая, что дифференциал аргумента может быть приравнен его приращению, окончательно для принятых зависимостей (2.31) получим расчетное выражение для определения дифференциала (приращения) водоизмещения судна-прототипа.
Рассмотренный способ определения водоизмещения судна является приближенным, поскольку в его основе лежит условие (2.27). Разность между приращением водоизмещения и его дифференциалом, а, следовательно, и погрешность метода будет тем меньше, чем меньше приращение (разница) между соответствующими характеристиками проектируемого судна и судна-прототипа. Погрешность получается приемлемой, если приращения, например скорость, не превышает 5¸10%. Другой причиной приближенности метода является то, что при расчете соответствующих производных используются данные судна-прототипа. Одновременно надо еще раз отметить, что специальным преимуществом дифференциального метода является то, что ошибка из-за неточности исходных формул, как из-за пренебрежения производными высших порядков, происходит только в рамках определения приращений искомых величин. В данном случае при определении D 1 D, тогда как основная часть искомой величины определяется практически точно по данным уже существующего судна-прототипа.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1796; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.120.64 (0.015 с.) |

 ) N + DW° + D LBТrd,
) N + DW° + D LBТrd,
 ) N + DW°,
или В 3 [(1–D) l br d – y к l b с ] = (
) N + DW°,
или В 3 [(1–D) l br d – y к l b с ] = ( .
. .
.
 .
.

 .
.
 ;
;
 .
.
 То есть в данном случае коэффициент h грпоказывает, что 71,3% от полной массы судна приходится на перевозимый груз. Естественно, что чем выше коэффициент утилизации при прочих равных условиях, тем лучше рассматриваемый вариант судна. Из сказанного вытекает первое направление использования этих коэффициентов – оценивать по доле полезной нагрузки качество проекта судна. При этом для специалиста коэффициент утилизации водоизмещения скажет не только о транспортном потенциале спроектированного варианта судна. В случае если его величина будет существенно отличаться в ту или другую сторону от средних значений для рассматриваемого типа судна, появятся основания для анализа причин этого, поиска возможных ошибок, допущенных при разработке проекта.
То есть в данном случае коэффициент h грпоказывает, что 71,3% от полной массы судна приходится на перевозимый груз. Естественно, что чем выше коэффициент утилизации при прочих равных условиях, тем лучше рассматриваемый вариант судна. Из сказанного вытекает первое направление использования этих коэффициентов – оценивать по доле полезной нагрузки качество проекта судна. При этом для специалиста коэффициент утилизации водоизмещения скажет не только о транспортном потенциале спроектированного варианта судна. В случае если его величина будет существенно отличаться в ту или другую сторону от средних значений для рассматриваемого типа судна, появятся основания для анализа причин этого, поиска возможных ошибок, допущенных при разработке проекта.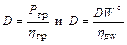 .
. .
.
 .
.



 , окончательно можно записать
, окончательно можно записать

 и q пропульсивного комплекса.
и q пропульсивного комплекса. ,
,
 – сумма производных высшего (n ³ 2) порядка, помноженная на коэффициенты, соответствующие степени приращения аргументов.
– сумма производных высшего (n ³ 2) порядка, помноженная на коэффициенты, соответствующие степени приращения аргументов.



 t, … a, b. c)
t, … a, b. c)
 , изменяется автономность судна по запасам топлива t = to + D t, а также предусматривается иная сумма независимых масс
, изменяется автономность судна по запасам топлива t = to + D t, а также предусматривается иная сумма независимых масс  Кроме того, по соображениям самого проектанта могут оказаться измененными параметры а, б, с, которые получают свои приращения. Тогда в соответствии с (2.27) приращение водоизмещения может быть найдено как полный дифференциал от уравнения масс (2.28)
Кроме того, по соображениям самого проектанта могут оказаться измененными параметры а, б, с, которые получают свои приращения. Тогда в соответствии с (2.27) приращение водоизмещения может быть найдено как полный дифференциал от уравнения масс (2.28)
 , dt, dPH – отождествляем с соответствующими конечными приращениями D v, D
, dt, dPH – отождествляем с соответствующими конечными приращениями D v, D  ).
).



 .
.












