
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обеспечение ходкости при проектировании суднаСодержание книги
Поиск на нашем сайте
Наряду с другими качествами судно должно обладать хорошей ходкостью, то есть должно двигаться с заданной скоростью при минимальных затратах мощности энергетической установки. Уровень этого важнейшего навигационного качества зависит от сопротивления внешней среды, действующей на судно во время его движения, эффективности движителя и взаимодействия системы «корпус-двигатель-движитель». Величина сопротивления движению судна зависит от размерений судна, формы его корпуса (соотношения главных размерений, коэффициентов полноты, формы обводов). Совместно с параметрами движителя они определяют необходимую мощность энергетической установки, которую необходимо знать уже при обосновании главных размерений и водоизмещения судна, хотя бы в первом приближении. Поэтому, говоря об обеспечении ходкости на начальных стадиях, задача сводится, прежде всего, к определению необходимой мощности судовой энергетической установки. Проблема состоит в том, что на рассматриваемых этапах проектирования судна отсутствует необходимая информация, которая могла бы позволить использовать известные методы теории корабля для оценки ходкости. поэтому вынуждены применять методы, использующие ограниченное число исходных данных, и, естественно, поэтому достаточно приближенные. В настоящее время получено достаточно много приближенных формул, позволяющих оценить мощность главных двигателей, необходимой для обеспечения заданной скорости хода. В зависимости от состава входящих в них исходных данных по судну эти формулы можно объединить в четыре группы. Все они в той или иной мере являются империческими, поскольку получены с использованием данных по ходкости соответствующих групп судов. Формулы первой группы. Это наиболее приближенные формулы, поскольку они связывают мощность энергетической установки только с ограниченным числом основных элементов и характеристик, чаще всего со скоростью хода и водоизмещением судна. Наиболее известным примером такого подхода является формула адмиралтейского коэффициента. Получается она исходя из следующего. Мощность, необходимая непосредственно на движение судна с заданной скоростью, или так называемая буксировочная мощность, равна произведению N d = R v, кВт, где R – полное сопротивление движению, кН; v – скорость хода, м/сек. Мощность двигателя, сообщающего судну скорость v
где c – число винтов; h пр – пропульсивный коэффициент полезного действия движительного комплекса; h вр – коэффициент полезного действия валопровода и передачи (редуктора). Пропульсивный кпд включает в себя коэффициент полезного действия винта hв, работающего в равномерном свободном, без присутствия корпуса судна потоке, а так же коэффициенты, учитывающие неравномерность потока и влияние корпуса на винт h пр = h в h к i, i - коэффициент неравномерности потока. Коэффициент влияния корпуса h к учитывает эффект засасывания винта, то есть увеличение сопротивления движению корпуса судна вследствие уменьшения давления в его кормовой части из-за разряжения возникающего на засасывающей поверхности лопасти работающего винта. Кроме того, h к включает в себя, так называемый, коэффициент попутного потока, который позволяет получить действительную скорость винта относительно воды
где t – коэффициент засасывания; y – коэффициент попутного потока. Полное сопротивление движению судна можно представить R = R г + R q, где R г – гидродинамическое сопротивление голого корпуса; R q – дополнительное сопротивление. Сопротивление R q учитывающие сопротивление выступающих частей, аэродинамическое сопротивление составляет некоторую долю c от сопротивления корпуса R = R г + c R г = (1 + c) R г. Тогда мощность главных двигателей в соответствии с (8.1) будет
Сопротивление голого корпуса в соответствии с квадратичным законом можно записать
где Величину смоченной поверхности представим по формуле Тейлора
где k т – коэффициент пропорциональности; V – объем водоизмещения. Выражение (8.2) преобразуем следующим образом
где l – относительная длина судна. Тогда
или
где С¢а – так называемый адмиралтейский коэффициент,
Формулу (8.3) в практике обычно применяют в следующем виде
В таком случае адмиралтейский коэффициент будет
Очевидно, что на стадиях обоснования элементов и характеристик судов определить Ca по (8.6) из-за отсутствия соответствующих данных не представляется возможным. Поэтому его либо принимают по судну-прототипу, либо используют соответствующую статистику. Но при этом надо иметь в виду, что результаты расчета мощности будут тем точнее, чем ближе совпадают у проектируемого судна и прототипа величины, входящие в (8.4) или (8.6). Проанализируем их степень влияния на Са. Величина плотности воды r в колеблется мало. Несколько больше колеблется коэффициент k т, но его изменением, также как и различием для составляемых судов коэффициента с, учитывающим дополнительное сопротивление, можно пренебречь. В пределах одной скоростной группы при соответствующей отработке характеристик движителя пропульсивный коэффициент h пр, также и коэффициент h вр, тоже считать постоянным. Основная причина, которая может привести к отличию Са по сравнению с принятым по судну-прототипу является изменения у этих судов в коэффициенте полного сопротивления x и по относительной длине l. Обе эти величины зависят от скорости хода, а также формы и размеров корпуса судна. Значительные колебания адмиралтейского коэффициента Cа характерны как для одной и той же скорости разных судов, так и для разных скоростей одного и того же судна. Полагая, что по геометрии корпуса проектируемое судно и прототип должны быть довольно-таки близкие, погрешность в принятии величины Са по прототипу является следствием, прежде всего, различий в скоростях хода. Рядом автором предложены способы пересчета Са при переходе от прототипа к проектируемому судну. Так В.А. Лесюков [10] получил следующую формулу для определения Са путем корректировки С¢а прототипа (величины со штрихом относятся к судну-прототипу)
где k = 0,16 – для морских грузовых судов; k = 0,21 – для судов внутреннего плавания. m – коэффициент, характеризующий отношение безразмерных коэффициентов полного сопротивления прототипа и проектируемого судна, определяется по следующим аппроксимационным выражениям для грузовых судов
для пассажирских судов
Fr¢ – число Фруда по длине судна-прототипа. Как отмечалось выше, недостатком формулы (8.5) является зависимость адмиралтейского коэффициента Ca от скорости хода. Это, например, не позволяет ее использовать для расчета зависимости N = f ( v) при проектировании судна. Нестабильность Са заставило искать другие формулы, имеющие более стабильные коэффициенты, мало зависящие от водоизмещения и скорости хода. Наиболее продуктивным является подход, базирующийся на использовании формул (8.3) и (8.5), но c измененными показателями степени V и v. Их подбирают таким образом, чтобы стабилизировать значение коэффициента C mn
Так для судов объемным водоизмещением от 2100 до 5800 м3 и скоростью хода от 5 до 12 м/сек, В.В. Давыдов получил следующую формулу
где V – объемное водоизмещение, м3; N – мощность главных двигателей, кВт; v – скорость в узлах; C mn = 150 ± 10. Известен ряд формул такого типа. В работе [11] на основании обследования большой группы транспортных судов (более 1000 единиц) предлагаются следующие значения показателей степени
при которых коэффициент C mn = 5,17 ± 0,54 при v в метрах в секунду, N – в киловаттах, V – в кубических метрах. Для судов смешанного плавания Данг Хыу Фу получил C mn = 4,18 ± 0,35 (v – в метрах в секунду). Для судов с Fr ³ 0,3 хороший результат дает формула Энстли
где по А.И. Гайковичу и И.В. Челпанову C mn= 7,8 ± 1,8 при v – в метрах в секунду. Формулы второй группы включают в себя кроме водоизмещения и скорости хода некоторые главные размерения судна, в силу чего они являются более точными по сравнению с формулами первой группы. Такие формулы получают статистическим анализом соответствующих функционально связанных элементов и характеристик судов. Примером таких формул может быть выражение, предложенное для речных судов А.Б. Карповым
где N – мощность главных двигателей в лошадиных силах; v – скорость хода в км/ч; L – расчетная длина, м. Для морских судов известна формула Ф. Папмеля для буксировочной мощности
где V – водоизмещение, м3; L – расчетная длина, м; l к – поправочный коэффициент при L £ 100 м l к = 0,7+0,3 при L > 100 м l к = 1 х – коэффициент, учитывающий дополнительное сопротивление от выступающих частей при неодинаковом числе валов, при этом х = 1 для одновальных установок и соответственно х = 1,05, х = 1,075, х = 1,10 для двух, трех и четырехвальных установок; Y к=10 d Формулы третьей группы. Более точное определение потребной мощности главных двигателей может быть произведено в зависимости от мощности сопротивления судна и расчета пропульсивного коэффициента системы корпус-движитель
где R – сопротивление движению судна; ŋ – пропульсивный коэффициент полезного действия; c – число движителей. Сопротивление движению водоизмещающего судна при этом записывается в следующем виде
где R – полное сопротивление движению судна; r – плотность воды; S – смоченная поверхность корпуса судна; x тр – коэффициент сопротивления трения гладкой плоской поверхности; x шер – надбавка к коэффициенту сопротивления трения на шероховатость смоченной поверхности; R ост – остаточное сопротивление; R доп – дополнительное сопротивление. Сопротивление трения определяют через экстраполятор трения с достаточно высокой точностью по известным методикам, используемым и при классическом пересчете результатов модельных испытаний на натурное судна. При этом величина смоченной поверхности при отсутствии теоретического чертежа рассчитывается по приближенным формулам, варианты которых весьма полно опубликованным в работах по ходкости судов. Так для судов внутреннего плавания хороший результат дает формула А.Б. Карпова
а так же формулы ЦНИИЭВТа
Таким образом, основная проблема при этом исходе оценки мощности сводится к определению R ост, для чего используются различные приближенные методики, применимые на стадии обоснования главных элементов судна. Так, например, для речных судов А.Б. Карпов дает следующее выражение
Fr – число Фруда по длине. Ряд авторов предложили приближенные способы расчета коэффициента остаточного сопротивления, а через него, с использованием квадратичного закона, и самого остаточного сопротивления R ост = Величину коэффициента остаточного сопротивления для грузовых судов согласно методике ЦНИИЭВТа определяется по следующему выражению
где xd – базовый коэффициент остаточного сопротивления, определяется по графику в зависимости от числа Фруда и коэффициента полноты d. Наиболее широко при таком подходе используются различные способы пересчета x ост. Они и составляют в принятой классификации формулы четвертой группы. Так В.А. Лесюков приводит способ, в котором для учета влияния различий в форме корпуса проектируемого судна и судна-прототипа на x ост используются перестроенные графики И.В. Гирса. В соответствии с ним коэффициент остаточного сопротивления x ост определяется
где x' ост – коэффициент остаточного сопротивления судна-прототипа. Коэффициента влияния формы корпуса на остаточное сопротивление для рассчитываемого судна Кj, Кl, Кj и для судна-прототипа К¢j, К¢l, К¢В/Т определяются по графикам рис. 8.1, 8.2 и 8.3 при одном и том же числе Фруда, соответствующим скорости проектируемого судна. Пределы применимости этих графиков:
Рис. 8.1. График для определения коэффициента влияния отношения В/Т на остаточное сопротивление
Рис. 8.2. График для определения коэффициента влияния продольной полноты φ=d / b на остаточное сопротивление
Рис. 8.3. График для определения коэффициента влияния относительной длины корпуса
В качестве геометрических параметров, характеризующих форму корпуса судна приняты: В/Т – отношение ширины судна к осадке; Значения x¢ ост для основных типов серийных судов внутреннего плавания, принятые по данным [2], приведены в табл. 8.1¸8.4. Прототип следует принимать наиболее близкий к проектируемому судну по величине коэффициента j, затем Y и, наконец, по отношению В/Т. Заданием на проектирование, как правило, задается скорость хода судна на глубокой воде. Однако при определении эксплуатационно-экономических показателей и, в частности времени кругового рейса, необходимо знать действительную скорость хода судна на линии с учетом влияния на нее различных эксплуатационных факторов и, прежде всего, мелководья, поскольку на ограниченной глубине сопротивление воды существенно возрастает. Для учета влияния мелководья на сопротивление движению судна могут быть использованы методы, изложенные в специальной литературе, например, [12]. На начальных стадиях проектирования в соответствии с [10] сопротивление на мелководье можно определить
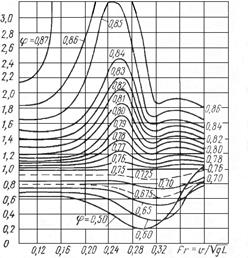
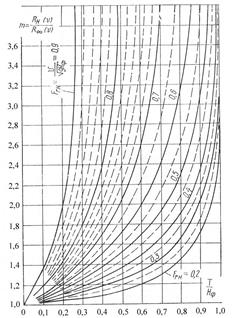
где Rн (v) – сопротивление воды на ограниченной глубине; Коэффициент увеличения сопротивления воды в докритическом режиме движения на мелководье m может быть найден по графику, приведенному на рис. 8.4 в зависимости от отношения Т/Н ф (где Н ф – глубина судового хода), характеризующего степень мелководья, и числа Фруда по глубине Fr н.
Рис. 8.4 Коэффициент увеличения сопротивления воды m при движении судна на мелководье
9. Методология определения основных элементов проектируемого судна
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.62.10 (0.013 с.) |


 ,
,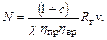
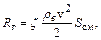
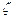 – коэффициент полного сопротивления; r в – плотность воды, S с м – смоченная поверхность корпуса судна.
– коэффициент полного сопротивления; r в – плотность воды, S с м – смоченная поверхность корпуса судна.



 ,
,
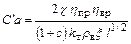 .
.
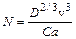
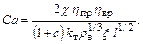
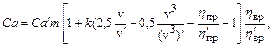
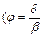 > 0,75)
> 0,75)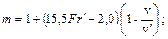

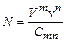 или
или 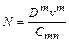 .
.
 ,
, ,
,

 ,
,
 ,
, (здесь d – коэффициент полноты водоизмещения, В/L – отношение ширины корпуса к расчетной длине судна); С – имперический коэффициент, определяемый по графику в зависимости от характеристики остроты Y к и приведенной скорости
(здесь d – коэффициент полноты водоизмещения, В/L – отношение ширины корпуса к расчетной длине судна); С – имперический коэффициент, определяемый по графику в зависимости от характеристики остроты Y к и приведенной скорости 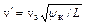 (vs – скорость хода в узлах).
(vs – скорость хода в узлах).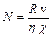 ,
,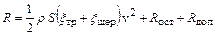
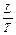 – 0,4 d),
– 0,4 d),
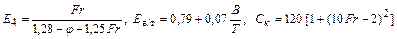
 x ост r S v2.
x ост r S v2.
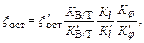
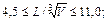 0,50 £ j £ 0,85; 1,5 £ В/Т £ 15,0.
0,50 £ j £ 0,85; 1,5 £ В/Т £ 15,0.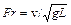


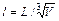 на остаточное сопротивление
на остаточное сопротивление – относительная длина судна;
– относительная длина судна; 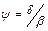 – призматический коэффициент продольной полноты.
– призматический коэффициент продольной полноты.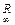 (v),
(v),
 0,32
0,32
 Коэффициент остаточного сопротивления x ост ×103
при числах Фруда
Коэффициент остаточного сопротивления x ост ×103
при числах Фруда
 Коэффициент остаточного сопротивления x ост ×103 при числах Фруда
Коэффициент остаточного сопротивления x ост ×103 при числах Фруда
 Коэффициент остаточного сопротивления x ост ×103
при числах Фруда
Коэффициент остаточного сопротивления x ост ×103
при числах Фруда



