
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение остойчивости и его анализСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Чтобы установить связь характеристик остойчивости с главными размерениями судна рассмотрим известное выражение для начальной метацентрической высоты
где r o – метацентрический радиус, м; zc, z g – аппликаты центра величины и центра тяжести судна, м. Величина метацентрического радиуса определяется
где Ix – момент инерции площади ватерлинии относительно продольной оси; V – объемное водоизмещение судна. Если полагать, что форма корабельной ватерлинии заключена между двух крайних по форме – прямоугольной и ромбической (a = 0,5), для которых соответственно
Найдем показатель степени n, удовлетворяющий граничным условиям (прямоугольной и ромбической ватерлиниям). Для ватерлинии в виде ромба (a = 0,5) согласно (5.4) можно записать
или
откуда n=2. Для прямоугольной ватерлинии (a = 1) условие Следовательно, удовлетворяя граничным условиям можно принять n = 2. Тогда подставив (5.4) в (5.3) метацентрический радиус будет
Однако реально ромбических ватерлиний в силу отсутствия у них требуемой плавности не бывает. Обеспечение их плавности приводит к S -образной ватерлинии, момент инерции которой несколько отличается от ромбической. Это обстоятельство в некоторой степени имеет место во всем диапазоне 0,5 < a < 1,0. Поэтому в выражение (5.5) вводится поправочный коэффициент Кr, с учетом которого получаем
Расчеты показывают, что для S -образных ватерлиний kr»1,06 ± 0,05, для выпуклых kr» 1,03 ± 0,05. А.П. Фан-дер-Флинт для ватерлиний описываемых параболой получил kr = 1,05, что привело к известной формуле
Поэтому в общем случае выражение (5.6) можно представить
Аппликата центра величины может быть определена в зависимости от осадки судна
Анализируя строевые по ватерлиниям Л.П.Эйлер и В.А. Поздюнин получили
Аналогичные решения получены и другими авторами [6], которые показывают, что kz зависит, прежде всего, от коэффициентов a и d. Поэтому в общем виде выражение (5.9) можно записать
Величина аппликаты центра тяжести судна связывается с его высотой борта
kg – коэффициент, характеризующий зависимость аппликаты центра тяжести от высоты борта, зависит от типа судна. Тогда, выражение для метацентрической высоты будет иметь вид
Разделив это выражение на ширину судна, получим, так называемое, уравнение остойчивости.
Обозначим
Из этого выражения видно, что основное влияние на остойчивость судна оказывает отношение В/Т. Поэтому рассматривая данный тип судна, можно поставить задачу определения значения В/Т, которое обеспечит требуемый уровень остойчивости h o. Для этого решим выражение (5.12) относительно b т, которое после приведения к общему знаменателю буде иметь вид
Положительный корень этого уравнения дает выражение
которое позволяет находить отношение В/Т, обеспечивающее требуемую остойчивость, задаваемую величиной Для целей анализа и предварительных оценок выражение (5.13) можно упростить. Примем вид функции fr (a,d) согласно (5.8)
Значение коэффициента полноты конструктивной ватерлинии можно представить
Тогда с учетом этого (5.14) примет значение fr (a, d) =0,084. Подставляя полученную величину в (5.13) получим
или подставив kg, a и d средние, например, для грузовых судов внутреннего плавания
Значение относительной метацентрической высоты для большинства судов внутреннего и смешанного плавания не превышает 0,25. Это позволяет величиной
Используя полученное выражение можно оценить изменение b т в результате изменения
или
Для малых конечных приращений в том случае, когда
Оценить влияние изменения b т на остойчивость судна можно по обратной зависимости
Как видно из полученного выражения, увеличить остойчивость можно за счет b т. Эти рассуждения справедливы для судна с принятым значением Н/Т, kg и коэффициентами полноты. Но это не означает, что при решении вопроса обеспечения остойчивости влиянием этих элементов судна следует пренебрегать. В более общем виде зависимость (5.20) приобретает вид
Отсюда видно, что неблагоприятное влияние первого слагаемого может быть компенсировано за счет второго. В частности приращение коэффициента kg может быть получено, например, за счет изменения числа ярусов надстройки или материала, из которого она изготавливается.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 893; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.123.41 (0.007 с.) |


 и
и  , то можно заключить, что момент инерции ватерлинии растает с увеличением коэффициента a. Для всех ватерлиний, лежащих между ромбической и прямоугольной момент инерции можно выразить
, то можно заключить, что момент инерции ватерлинии растает с увеличением коэффициента a. Для всех ватерлиний, лежащих между ромбической и прямоугольной момент инерции можно выразить


 выполняется при любом значении n.
выполняется при любом значении n.




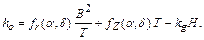

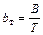 и, умножив и разделив вычитаемое на Т, будем иметь
и, умножив и разделив вычитаемое на Т, будем иметь


 . Кроме того, из выражения (5.13) видно, что уровень остойчивости судна прямопропорционален величине этого отношения. Он объясняет известное обстоятельство, что грузовые суда внутреннего и смешанного плавания, являющиеся относительно низкобортными и поэтому, имея сравнительно низкие значения аппликаты центра тяжести (коэффициент Кg» 0,65), обладают избыточной остойчивостью. Это является следствием того, что их отношение В/Т из-за ограничения по осадке принимает большие значения, например по сравнению с однотипными морскими судами, а в результате – высокий уровень остойчивости.
. Кроме того, из выражения (5.13) видно, что уровень остойчивости судна прямопропорционален величине этого отношения. Он объясняет известное обстоятельство, что грузовые суда внутреннего и смешанного плавания, являющиеся относительно низкобортными и поэтому, имея сравнительно низкие значения аппликаты центра тяжести (коэффициент Кg» 0,65), обладают избыточной остойчивостью. Это является следствием того, что их отношение В/Т из-за ограничения по осадке принимает большие значения, например по сравнению с однотипными морскими судами, а в результате – высокий уровень остойчивости.


 вследствие ее малости пренебречь. Тогда (5.16) примет вид
вследствие ее малости пренебречь. Тогда (5.16) примет вид
 и элементов судна, входящих во второе слагаемое формулы (5.18), для чего продифференцируем ее
и элементов судна, входящих во второе слагаемое формулы (5.18), для чего продифференцируем ее

 не изменяется
не изменяется





