
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Остойчивость на больших углах наклоненияСодержание книги
Поиск на нашем сайте Общие положения. В процессе изложения теории начальной остойчивости судна было отмечено, что определение восстанавливающего момента и плеча остойчивости метацентрическими формулами допустимо только при малых углах наклонения. При увеличении этих углов приходится прибегать к теории остойчивости на больших углах наклонения. Основы данной теории излагаются в настоящем параграфе, где рассматривается лишь остойчивость на больших углах крена, поскольку большой дифферент у неповрежденного судна практически никогда не возникает. Условимся, как и ранее, что в исходном равновесном положении судно сидит прямо и на ровный киль, его наклонение происходит в вертикальной поперечной плоскости, а деривационный момент, возникающий в процессе наклонения вследствие несимметрии судна относительно плоскости мидель-шпангоута уравновешивается некоторым воображаемым внешним моментом. Другими словами, будем рассматривать плоскую задачу поперечного наклонения судна, считая, что все характерные точки - ЦВ, ЦТ, метацентр, а также линии действия сил веса и плавучести представлены их проекциями на плоскость наклонения, совпадающую с координатной плоскостью yOz (рис. 2.21).
Рассмотрим равнообъемное наклонение судна на угол Θ; не налагая на его значение каких-либо ограничений. При таком наклонении ЦВ судна переместится в точку cθ, а сила веса и сила плавучести γV, действуя перпендикулярно новой ватерлинии ВθЛθ, составят пару сил. Плечо этой пары При наклонении судна на большой угол теорема Эйлера недействительна и ось наклонения уже не проходит через ЦТ площади начальной ватерлинии, отвечающей прямому положению судна. Кроме того, кривая ССθ уже не может считаться дугою круга; аналитического выражения она не имеет, и форма ее зависит от обводов судна. В общем случае поперечный метацентр mθ выходит из ДП и его положение определяется метацентрическим радиусом rθ =Ixθ /V, (2.69) где Ixθ - центральный момент инерции площади наклонной ватерлинии ВθЛθ относительно ее продольной оси. Если из ЦВ опустить перпендикуляр CN на линию действия силы плавучести судна в его наклонном положении, то плечо остойчивости можно представить как разность:
Отрезок lф называют плечом остойчивости формы, так как при данных водоизмещении судна и угле крена его значение зависит только от координат ЦВ, определяемых формой подводного объема. Отрезок lв = α sinθ называют плечом остойчивости веса, так как при данном угле крена его величина зависит только от возвышения α ЦТ над ЦВ. Соответственно момент Мф=Рlф называют моментом остойчивости формы, а момент МВ =РlВ = Pa sin θ - моментом остойчивости веса. Иногда в качестве плеча остойчивости формы
Рассмотренное выше разделение плеча остойчивости на две части имеет целью выделение той его части (плеча веса), которая зависит от данного состояния нагрузки судна и, следовательно, может быть определена только на судне после его погрузки. Оставшаяся же часть (плечо формы) может быть рассчитано заранее в функции водоизмещения и угла крена, а результаты такого расчета могут быть выданы на судно в виде соответствующих графиков. Диаграмма статической остойчивости. Кривую, выражающую зависимость плеча статической остойчивости l или восстанавливающего момента МВ=Рl от угла крена θ называют диаграммой статической остойчивости или диаграммой Рида по имени английского корабельного инженера, впервые предложившего ее для оценки остойчивости судна на больших углах крена. По оси абсцисс диаграммы откладывают значения угла крена: положительные (на правый борт) вправо и отрицательные (на левый борт) влево от начала координат, а по оси ординат - значение плеча остойчивости или восстанавливающего момента (рис. 2.22). Поскольку диаграмму остойчивости строят для некоторого определенного водоизмещения судна, между плечом остойчивости и восстанавливающим моментом существует прямая пропорциональная зависимость и, следовательно, одна и та же кривая может служить одновременно диаграммой моментов и диаграммой плеч остойчивости - изменяется только масштаб ее ординат. В таких случаях говорят, что диаграмма остойчивости построена „в плечах" или „в моментах".
В силу симметрии судна относительно ДП обычно ограничиваются построением только одной половины диаграммы остойчивости для положительных значений угла крена - на правый борт. Остойчивость на малых углах крена можно рассматривать, очевидно, как частный случай остойчивости на больших углах крена. Следовательно, диаграмма статической остойчивости должна характеризовать некоторым образом также начальную поперечную остойчивость судна. Действительно, дифференцируя по углу крена θ приближенную (метацентрическую) формулу для плеча статической остойчивости l ≈ h sin θ, получаем
При θ = 0 эта производная принимает точное значение:
Таким образом, в начальном (прямом) положении судна производная плеча статической остойчивости по углу крена численно равна начальной поперечной метацентрической высоте. Но, как известно из аналитической геометрии, производная функции геометрически выражает угловой коэффициент касательной в данной точке к графику функции, т. е. тангенс угла между этой касательной и положительным направлением оси абсцисс. Следовательно, для изображения начальной метацентрической высоты на диаграмме плеч статической остойчивости можно воспользоваться следующим построением (рис. 2.23): по оси абсцисс откладывают от начала координат отрезок ОА, равный в масштабе углов крена 1 рад, затем в точке А восстанавливают перпендикуляр к оси абсцисс, который пересекается в точке В с касательной к диаграмме, проведенной в начале координаn. Отрезок АВ этого перпендикуляра, измеренный в масштабе плеч остойчивости, будет равен начальной метацентрической высоте. В самом деле, из прямоугольного треугольника ОБА находим
Соответственно, если диаграмма остойчивости построена в моментах, то производная восстанавливающего момента по углу крена при θ = 0 будет численно равна коэффициенту поперечной остойчивости k=Ph. Рисунок 2.23 наглядно показывает допустимые пределы использования метацентрической формулы (2.10), графиком которой является касательная 0В. При малых θ прямая ОВ и кривая ОСЕ, выражающая действительный закон изменения плеча статической остойчивости по углу Θ, практически совпадают. Резкое расхождение между ними начинается обычно после входа в воду кромки палубы или выхода из воды скулы судна.
При положительной начальной остойчивости характерными точками диаграммы являются точка О - положение устойчивого равновесия судна - и точки В и В', расположенные симметрично относительно начала координат и определяющие углы заката диаграммы Θ3, при которых судно находится в положениях неустойчивого равновесия (см. рис. 2.22). При углах крена, меньших угла заката, судно остойчиво, поскольку восстанавливающий момент стремится вернуть его в положение устойчивого равновесия О. Наибольшую по абсолютному значению ординату диаграммы, определяемую точками А или А', называют максимальным плечом диаграммы (или максимальным восстанавливающим моментом), а отвечающий этой ординате угол крена - углом максимума диаграммы остойчивости. Наибольшая ордината диаграммы соответствует предельному статическому кренящему моменту, приложение которого еще не вызывает опрокидывания судна. На рис. 2.24 приведены типичные диаграммы статической остойчивости для низкобортного судна с большой начальной остойчивостью и высокобортного судна с малой начальной остойчивостью.
Рис. 2.24. Типичные формы диаграммы статической остойчивости: α — низкобортного судна; б — высокобортного судна На рис. 2.25 изображена диаграмма статической остойчивости судна, имеющего отрицательную начальную остойчивость (в прямом положении). В этом случае положениям неустойчивого равновесия судна будут отвечать не только точки заката диаграммы В и В', но и начало координат О. Положениям устойчивого равновесия будут соответствовать две точки - С и С'. Таким образом, судно с отрицательной начальной остойчивостью не может свободно плавать в прямом положении; оно будет иметь крен θ1на правый борт или равный ему крен θ’1 на левый борт в зависимости от случайных внешних причин (ветра, волнения, перекладки руля и т. п.). Наличие отрицательной начальной остойчивости еще не может служить основанием для заключения, что данное судно вообще неостойчиво и должно опрокинуться. Судно опрокидывается только в том случае, когда его диаграмма остойчивости примет вид, показанный на рис. 2.25 штриховой линией, и будет пересекать ось абсцисс только в одной точке - в начале координат О.
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1029; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

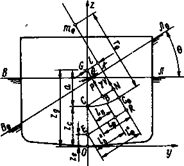 Рис. 2.21. Наклонение судна на большой угол
Рис. 2.21. Наклонение судна на большой угол = l, как и ранее, при рассмотрении малых наклонений назовем плечом статической остойчивости, а момент Мв = Рl - восстанавливающим моментом судна.
= l, как и ранее, при рассмотрении малых наклонений назовем плечом статической остойчивости, а момент Мв = Рl - восстанавливающим моментом судна.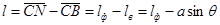 . (2.70)
. (2.70)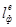 принимают перпендикуляр ER, опущенный на линию действия силы плавучести из полюса Е, расположенного неподвижно в ДП судна. Тогда плечо остойчивости веса равно
принимают перпендикуляр ER, опущенный на линию действия силы плавучести из полюса Е, расположенного неподвижно в ДП судна. Тогда плечо остойчивости веса равно 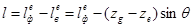 . (2.71)
. (2.71)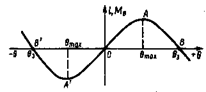 Рис. 2.22. Диаграмма статической остойчивости
Рис. 2.22. Диаграмма статической остойчивости (2.72)
(2.72)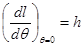 (2.73)
(2.73)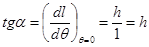 (2.74)
(2.74)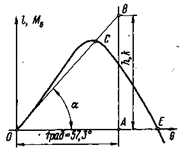 Рис. 2.23. Начальная остойчивость на диаграмме статической остойчивости
Рис. 2.23. Начальная остойчивость на диаграмме статической остойчивости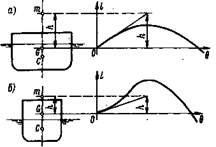
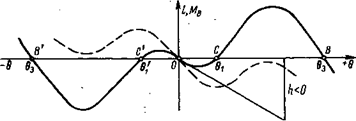 Рис. 2.25. Диаграмма статической остойчивости
Рис. 2.25. Диаграмма статической остойчивости


