
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение диаграммы статической остойчивости и практическое ее использованиеСодержание книги
Поиск на нашем сайте Задача о построении диаграммы статической остойчивости с использованием ЭВМ при максимальной автоматизации ввода исходных данных в принципе решена. Однако в настоящее время до осуществления массового (серийного) изготовления бортовых ЭВМ с соответствующими устройствами и снабжения ими судов морского флота для построения диаграмм статической остойчивости могут служить в качестве вспомогательных материалов интерполяционные кривые плеч остойчивости формы, пантокарены и универсальные диаграммы остойчивости, содержащиеся в комплекте судовой документации. Интерполяционные кривые плеч остойчивости формы и пантокарены. При заданных обводах корпуса плечи формы lф можно рассматривать как функцию двух переменных - объемного водоизмещения V и угла крена θ: lф = f(V,θ). (2.75) Если в уравнении (2.75) положить θ = θi = const, плечо формы становится функцией одного переменного lф=f(V). Кривые lф=f(V) называют интерполяционными кривыми плеч остойчивости формы. Их строят в конструкторских бюро для ряда углов крена от 0 до 90° (с интервалами 10°) для водоизмещении, лежащих в пределах, представляющих практический интерес, т.е. от водоизмещения порожнего судна Vnop до водоизмещения судна с полным грузом Vгр (рис. 2.26). С помощью интерполяционных кривых плеч остойчивости формы можно построить диаграмму статической остойчивости судна для любого состояния его нагрузки. Для этого на оси абсцисс интерполяционных кривых откладывают точку, соответствующую данному водоизмещению, восставляют в ней перпендикуляр и снимают с кривых значения l ф для углов крена 10°, 20° и т. д. Дальнейшее вычисление плеч статической остойчивости производят по формуле l = lф – a sin θ = lф – (zg-zc)sin θ (2.76) При этом аппликату ЦТ судна zg находят из расчета нагрузки, отвечающей данному водоизмещению, а аппликату ЦВ zc - по соответствующей кривой, имеющейся в документе “Кривые элементов теоретического чертежа”. После определения всех плеч формы строят кривую l фи синусоиду α sin θ, разности ординат которых являются плечами статической остойчивости (рис. 2.27). Если плечи остойчивости формы l ф отсчитываются от полюса Ε (см. рис. 2.21), то соответствующие кривые l ф = f (V) носят название пантокарен. При помощи пантокарен диаграммы статической остойчивости строят так же, как при помощи кривых плеч остойчивости формы. Универсальная диаграмма статической остойчивости. Для быстрого построения диаграммы статической остойчивости в судовых условиях наряду с интерполяционными кривыми плеч остойчивости формы и пантокаренами используют универсальную диаграмму остойчивости, которую чертят в конструкторском бюро и включают в состав вспомогательных материалов для самостоятельных расчетов, содержащихся в Информации об остойчивости. Различными авторами были предложены различные формы универсальной диаграммы, включаемой в Типовую информацию об остойчивости и прочности грузового судна, при использовании которой исходными данными являются фактический дедвейт судна и начальная метацентрическая высота судна при данном состоянии его нагрузки.
Рис. 2.26. Пантокарены Рис. 2.27. Построение диаграммы статической остойчивости с помощью пантокарен Теоретические основы универсальной диаграммы статической остойчивости заключаются в следующем: к выражению (2.76) для плеча статической остойчивости прибавляют и одновременно вычитают из него одну и ту же величину hcpsin θ и, принимая во внимание, что a=r-h, представляют это выражение в следующей форме: l = lф – (r - h)sin θ + hcpsin θ - hcpsin θ (2.77) где hcp - некоторое произвольное приблизительно среднее для данного судна значение начальной метацентрической высоты. Если положить = lф – r sin θ + hcpsin θ (2.78) l`в = (h - hcp) sin θ (2.79) то выражение (2.77) принимает вид l= l`ф + l`в (2.80) При некотором заданном угле крена θ первое слагаемое - условное плечо формы l`ф - зависит только от формы подводного объема данного судна, а следовательно, от его водоизмещения или дедвейта, а второе слагаемое - условное плечо веса l`в - только от его начальной метацентрической высоты. При построении универсальной диаграммы вычерчивают два семейства кривых: условных плеч формы l`ф для ряда значений дедвейта судна и условных плеч веса l`в для ряда значений начальной метацентрической высоты от h = 0 до некоторого ее значения, которое для данного судна является наибольшим (рис. 2.28). Для того чтобы кривые l`в представляли собой не синусоиды, а пучок прямых линий, выходящих из начала координат (что упрощает построение диаграммы), шкалу углов крена принимают синусоидальной, т. е. на оси абсцисс диаграммы наносят деления, расстояния которых от начала координат пропорциональны не углам крена, а синусам этих углов. Диаграмма статической остойчивости для любого заданного значения дедвейта и любой метацентрической высоты видна непосредственно на универсальной диаграмме. Например, на рис. 2.28 показана жирной линией диаграмма статической остойчивости для Δw = 4600 т и h = 0,7 м при hср = 1,0 м. При желании эту диаграмму можно легко перестроить в обычную форму, откладывая плечи остойчивости от горизонтальной оси и пользуясь обычной шкалой углов крена.
Практическое использование диаграммы статической остойчивости. Диаграмму статической остойчивости, построенную для данного состояния нагрузки судна, во-первых, используют для того, чтобы подтвердить выполнение требований Регистра СССР к остойчивости судна на больших углах крена, изложенных ниже. Такое подтверждение может стать необходимым в тех случаях, когда нагрузка судна не соответствует типовой (предусмотренной Информацией об остойчивости) и его остойчивость вызывает сомнения.
Рис. 2.29. Применение диаграммы статической остойчивости для определения угла крена судна при горизонтально-поперечном переносе груза
Во-вторых, с помощью диаграммы статической остойчивости может быть определен крен судна тогда, когда метацентрическая формула, пригодная только для малых углов крена, оказывается неприменимой. Для нахождения угла крена на диаграмме статической остойчивости строят кривую кренящего момента Мкр =f(θ) или кренящего плеча lкp = Mкp/P= f(θ). Точки пересечения этой кривой с диаграммой остойчивости определят положения устойчивого и неустойчивого равновесий судна. Например, кренящее плечо при горизонтально-поперечном переносе груза на расстояние у 2 – у1 выражается зависимостью lкр=Р(y2-y1)соsθ/Р. (2.81) Углу статического крена θ1 (положение устойчивого равновесия) будет соответствовать точка А пересечения косинусоиды (2.81) с диаграммой остойчивости (рис. 2.29). Точка В определит угол θ2, отвечающий положению неустойчивого равновесия. Динамическая остойчивость Общие положения. Динамической остойчивостью называют способность судна выдерживать, не опрокидываясь, динамическое воздействие кренящего момента. Задача о крене судна при воздействии на него кренящего момента была рассмотрена выше в статической постановке, т. е. анализировалось положение судна, при котором наблюдается статическое равновесие между кренящим и восстанавливающим моментами. Предполагалось, что кренящий момент прикладывается к судну постепенно, вызывая пренебрежимо малые ускорения, либо что с момента его приложения истекло достаточно много времени. Значительный практический интерес представляет рассмотрение той же задачи в динамической постановке, когда нарастание кренящего момента до его наибольшего значения происходит в течение очень короткого времени, не соизмеримого со временем накренения судна, или практически мгновенно. Так действует, например, на судно внезапно налетевший порыв ветра (шквал). В каждый момент времени при этом не будет наблюдаться равенства между кренящим и восстанавливающим моментами, и судно получит так называемый динамический крен, кратковременный, но значительно больший крена, возникающего при статическом действии такого же кренящего момента. Рассмотрим процесс наклонения судна под действием внезапно приложенной внешней кренящей пары сил, продолжающей действовать неограниченно долго после приложения. В целях упрощения задачи будем считать, что момент этой пары Мкр не зависит от угла крена (в частности, для ветрового момента это приблизительно соответствует действительности). В этом случае график кренящего момента изобразится на диаграмме остойчивости прямой линией АС, параллельной оси θ (рис. 2.30). На участке наклонения судна АВ кренящий момент больше восстанавливающего, и судно будет крениться с нарастающей угловой скоростью и убывающим угловым ускорением, которое обратится в нуль в точке В, т. е. при достижении статического угла крена θст. Однако угловая скорость накренения в этом положении судна достигнет максимума, поэтому оно не остановится, а будет продолжать крениться по инерции с убывающей угловой скоростью, которая наконец обратится в нуль в некоторой точке Е при достижении динамического угла крена θдин. Эта точка не является положением равновесия, так как восстанавливающий момент в ней больше кренящего; поэтому судно задержится в ней лишь на одно мгновение, а затем его крен будет убывать и рассмотренный процесс повторится в обратном направлении, т. е. судно начнет совершать колебательные движения, постепенно затухающие под влиянием сопротивления среды. Размахи колебаний судна будут при этом постепенно уменьшаться и, наконец, оно придет в положение статического равновесия с углом крена θст.
В процессе колебаний судна происходит непрерывный переход кинетической энергии его накренения в потенциальную, и наоборот. Следовательно, наибольший угол динамического крена может быть определен из условия равенства работ кренящего и восстанавливающего моментов при накренении от θ = 0 до θ = θдин (сопротивлением среды, а следовательно, и его работой при этом пренебрегают). Известно, что работа пары сил выражается произведением ее момента на угол поворота, а при переменном моменте - площадью под его графиком, построенным в функции угла поворота. В данном случае математическим выражением указанного равенства работ будет служить уравнение
Подынтегральная функция в правой части уравнения (2.82) не может быть выражена аналитически, поэтому это уравнение может быть решено относительно θдин только графическим способом - таким подбором положения ординаты DF, при котором площади, выраженные правой и левой частями уравнения, будут равны, т. е. площадь OAEF = площадь OBDF. (2.83) Обе площади включают общую для них площадь OBEF, следовательно, условие для подбора ординаты DF можно записать в виде равенства площадей, заштрихованных на рис 2.30: площадь OAB = площадь BDE. (2.84) Предельный динамический кренящий момент, действие которого судно способно выдержать не опрокидываясь (называемый обычно опрокидывающим моментом), определится равенством заштрихованных площадей ОАВ и BCD (рис. 2.31). Этому моменту соответствует предельный динамический угол крена θдин.пред.
Из сказанного следует, что мерой динамической остойчивости судна служит работа Т восстанавливающего момента при наклонении судна от Начального равновесного положения до некоторого заданного угла крена. Эта работа равна
В практике получила также распространение относительная мера динамической остойчивости - отношение работы восстанавливающего момента к силе веса судна, называемое плечом динамической остойчивости
В теории судна доказывается, что плечо динамической остойчивости имеет размерность длины и определенный геометрический смысл: оно равно приращению возвышения ЦТ над ЦВ судна при его равнообъемном наклонении из прямого положения до заданного угла крена θ (рис. 2.32). Действительно, работа восстанавливающего момента равна работе сил веса и плавучести при наклонении судна, которая, в свою очередь, равна произведению одной из этих сил на приращение расстояния между ними.
Диаграмма динамической остойчивости. Кривую, выражающую зависимость работы восстанавливающего момента (или плеча динамической остойчивости) от угла крена, называют диаграммой динамической остойчивости.
Формулы (2.85) и (2.86) показывают, что диаграмма динамической остойчивости является интегральной кривой по отношению к диаграмме статической остойчивости (рис. 2.33) и поэтому обладает следующими свойствами, общими для всех интегральных кривых: - точки пересечения подынтегральной кривой (диаграммы статической остойчивости) с осью абсцисс отвечают точкам О и D экстремума интегральной кривой (диаграммы динамической остойчивости); - точка А максимума диаграммы статической остойчивости соответствует точке перегиба С диаграммы динамической остойчивости; - любая ордината диаграммы динамической остойчивости, отвечающая некоторому углу крена θ, представляет в масштабе соответствующую этому углу крена площадь диаграммы статической остойчивости (заштрихована на рисунке). Рабочая форма вычисления ординат диаграммы динамической остойчивости приведена в табл. 2.1. Таблица 2.1. Вычисление ординат диаграммы динамической остойчивости
δ θ/2 = 10°/2 = 0,1745/2 = 0,0873 рад Диаграмму динамической остойчивости целесообразно использовать в судовых условиях для решения двух рассмотренных выше задач: определения динамического угла крена при заданном динамическом кренящем моменте и определения опрокидывающего момента. Приведенное выше решение этих задач при помощи диаграммы статической остойчивости, хотя и наглядно, но методически не вполне удобно, так как требует довольно трудоемкого подбора ординат, обеспечивающих равенство известных площадей. При использовании диаграммы динамической остойчивости это неудобство устраняется. Рассмотрим диаграмму динамической остойчивости, построенную в плечах lдин, (рис.2.34), и соответственно графическое решение уравнения, аналогичного уравнению (2.82),
где l кр = Мкр /Р - плечо кренящего момента. Динамический кренящий момент принимается постоянным по углам крена. Следовательно, его работа находится в линейной зависимости от угла θ, а график произведения lκρθ =f(θ) изобразится на диаграмме динамической остойчивости прямой наклонной линией. В наиболее простом случае, когда рассматривается воздействие динамического кренящего момента на судно, находящееся в прямом равновесном положении, эта прямая будет проходить через начало координат. Для ее построения достаточно провести вертикаль через точку, отвечающую крену в 1 рад (57,3°), и отложить на этой вертикали заданное кренящее плечо lκρ. Прямая, соединяющая найденную таким образом точку Ε с началом координат 0, представит искомый график произведения lκρθ, т.е. график работы кренящего момента, отнесенной к силе веса судна Р. Эта прямая пересечет диаграмму динамической остойчивости в двух точках: А и В. Абсцисса первой из этих точек определяет угол динамического крена θдин, при котором имеет место равенство работ кренящего и восстанавливающего моментов. Вторая точка пересечения практического значения не имеет.
Если построенный таким образом график произведения lκρθ вообще не пересекает диаграмму динамической остойчивости, то это означает, что судно опрокидывается. Для того чтобы найти предельный кренящий момент Мопр, который судно еще может выдержать не опрокидываясь, следует провести из начала координат касательную к диаграмме динамической остойчивости до пересечения ее в точке D с вертикалью, соответствующей крену в 1 рад. Отрезок этой вертикали от оси θ до пересечения ее с касательной определит плечо опрокидывающего момента l опр, а сам момент определится умножением плеча lопр на силу веса судна Р. Точка касания С определит предельный угол динамического крена θдин.пред. Рассмотренное выше решение задачи определения опрокидывающего момента несколько идеализирует физическую картину явления применительно к воздействию на судно кренящего момента от налетевшего шквала ветра. В реальных условиях судно, как правило, воспринимает действие ветра, находясь в открытом море и испытывая бортовую качку. Поэтому Правила Регистра СССР (часть IV „Остойчивость") предписывают использовать следующую методику определения опрокидывающего момента с учетом качки. На диаграмме динамической остойчивости находят вспомогательную точку А (рис. 2.35). Для этого вправо от начала координат откладывают максимальную амплитуду бортовой качки (определяемую по приводимой в Правилах методике) и на кривой динамической остойчивости фиксируют соответствующую точку А', через которую проводят прямую, параллельную оси абсцисс. На этой прямой влево от вспомогательной точки А откладывают отрезок АА', равный двойной амплитуде качки (АА'=2θr). Найденная таким образом точка А, расположенная симметрично точке А', определяет начало динамического процесса накренения судна под действием динамического кренящего момента. Далее из точки А проводят касательную АС к диаграмме динамической остойчивости и от точки А на прямой, параллельной оси абсцисс, откладывают отрезок АВ, равный 1 рад. В точке В восставляют перпендикуляр BE до пересечения с касательной АС. Отрезок BE равен плечу опрокидывающего момента lопр = Мопр/Р, еслидиаграмма динамической остойчивости построена в масштабе плеч, как на рис. 2.35, или равен опрокидывающему моменту Мопр, если диаграмма построена в масштабе работ.
|
||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 2246; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.012 с.) |



 Рис. 2.28. Универсальная диаграмма статической остойчивости
Рис. 2.28. Универсальная диаграмма статической остойчивости
 Рис. 2.30. Действие внезапно приложенного кренящего момента
Рис. 2.30. Действие внезапно приложенного кренящего момента . (2.82)
. (2.82) Рис. 2.31. Определение опрокидывающего момента
Рис. 2.31. Определение опрокидывающего момента . (2.85)
. (2.85) . (2.86)
. (2.86)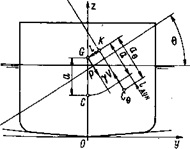 Рис. 2.32. К объяснению геометрического смысла плеча динамической остойчивости
Рис. 2.32. К объяснению геометрического смысла плеча динамической остойчивости Рис. 2.33. Диаграммы статической и динамической остойчивости
Рис. 2.33. Диаграммы статической и динамической остойчивости
 , (2.87)
, (2.87)
 Рис. 2.35. Определение опрокидывающего момента с учетом качки
Рис. 2.35. Определение опрокидывающего момента с учетом качки


