
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Влияние переноса, приема или снятия твердых и жидких грузов на посадку и начальную остойчивость суднаСодержание книги
Поиск на нашем сайте Влияние переноса твердых грузов на посадку и начальную остойчивость судна. Примем сначала допущение, что в исходном равновесном положении судно имеет посадку прямо и на ровный киль. Предположим далее, что в общем случае некоторый твердый груз массой m переносится на судне в произвольном направлении так, что его ЦТ перемещается из точки А (х1 у1 z1) в точку В (x2, y2, z2) так, как показано на рис. 2.10. Для того, чтобы определить влияние такого переноса груза на посадку и начальную остойчивость судна, воспользуемся следующим методом исследования. Располагая в точке А начало вспомогательной координатной системы A x yz, разложим перемещение АВ на три перемещения в направлениях координатных осей и будем рассматривать сначала влияние вертикальной составляющей перемещения груза (в направлении оси Az), азатем влияние горизонтально-поперечной и горизонтально-продольной составляющих (в направлениях осей Ау и Ах).
Перемещение груза вдоль оси Oz (рис. 2.11) не создает момента, способного вызвать наклонение судна, и, следовательно, его посадка при таком перемещении не изменится, если начальная остойчивость останется положительной и судно будет по прежнему находиться в состоянии устойчивого равновесия.
Приращения поперечной и продольной метацентрических высот определяем как суммы приращений их отдельных компонентов согласно формулам (2.7) и (2.8): δh = δzm - δzg; δΗ = δzΜ - δzg. (2.24) При неизменной посадке судна δzm = δzΜ = 0, поэтому δh = δH = - δzg. (2.25) Для определения приращения δzg аппликаты ЦТ судна может быть использована известная теорема теоретической механики: если в системе материальных тел одно из тел получит перемещение в каком-либо направлении, то ЦТ всей системы переместится в том же направлении, причем величины перемещений будут обратно пропорциональны массам тела и всей системы. Применительно к рассматриваемому случаю вертикального перемещения груза указанная теорема приводит к выражению Δzg = (m/Δ)(z2-z1) (2.26) где Δ - водоизмещение судна вместе с переносимым грузом; z1 и z2 -координаты ЦТ груза до и после переноса. Подставляя (2.26) в (2.25), получаем δh = H = -(m/Δ)(z2-z1) (2.27) Выражение (2.27) показывает, что перенос груза по вертикали вниз (z2<z1) приводит к увеличению остойчивости судна, а перенос по вертикали вверх - к ее уменьшению. При горизонтально-поперечном переносе груза (в направлении оси Оу) из точки А1(у1) в точку В1(у2) начальная остойчивость не изменится, так как ни аппликата метацентра, ни аппликата ЦТ судна не получат приращений (рис. 2.12). Однако посадка судна изменится - оно получит крен Θ. Заметим, что перенос груза на расстояние А1В1 можно представить как снятие груза из точки А1 и прием такого же груза в точку Вх. Приложив к судну в этих точках две равные, но противоположно направленные силы p = mg, видим, что перенос груза приводит к образованию пары сил на плече (у2 – y1)cos θ. Момент этой пары сил, являющийся кренящим моментом, равен Мкр = p(y2-y1)cos θ (2.28)
Рис. 2.12. Горизонтально- Рис. 2.13. Горизонтально-продольный поперечный перенос груза перенос груза Поскольку угол θ предполагается малым, можно принять cos θ Мкр = p(y2-y1) (2.29) Приравнивая (в равновесном наклонном положении судна) кренящий момент восстанавливающему Мв =P(h + δh)θ, находим
где δ h- приращение начальной метацентрической высоты, являющееся следствием рассмотренного ранее влияния вертикальной составляющей перемещения груза. При горизонтально-продольном переносе груза из точки В1(х1) в заданную точку В2(х2)(рис. 2.13) начальная остойчивость судна, как и в предыдущем случае, не изменится, но возникнет дифферент судна, угол которого по аналогии может быть найден в соответствии с формулой:
Практически важно знать не угол дифферента, который обычно весьма мал, а изменение осадок носом и кормой и дифферент судна. Проведем новую ватерлинию равновесия В1Л1 под углом ψ к первоначальной ватерлинии ВЛ. При малом угле ψ можно считать, что ватерлинии ВЛ и В1Л1 как равнообъемные пересекутся по оси, проходящей через их общий ЦТ F (xf).Тогда новые осадки носом и кормой будут равны dHl = d + (L/2 -xf)ψ; dK1 =(L/2 + xf)ψ. (2.32) Как было отмечено ранее, все полученные зависимости основаны на допущении, что судно до переноса груза сидело прямо и на ровный киль. Если же в действительности судно имело начальные (малые) углы крена и дифферента, то при определении новых углов крена и дифферента по формулам (2.30) и (2.31) в числители этих формул следует подставить алгебраические суммы моментов, возникающих в результате переноса груза, и моментов Ρhθ0 и ΡΗψ0, отвечающих начальным углам крена и дифферента. Выполнив это, получим
Формулы (2.33) показывают, что в этом случае даже при отсутствии перемещений груза в направлении осей Ох и Оу его перемещение в направлении оси Οz приводит не только к изменению начальной остойчивости судна, но и к появлению дополнительных углов крена и дифферента

Влияние подвешенного груза на начальную остойчивость судна. Предположим, что находящийся в трюме груз массой т поднимают судовым краном или стрелой (рис. 2.14). В момент отрыва от настила трюма груз становится подвешенным, и в этот же момент начальная метацентрическая высота мгновенно получает некоторое приращение δh. Для определения этого приращения мысленно наклоним судно на малый угол Θ. Тогда шкентель, на котором подвешен груз, примет положение, перпендикулярное плоскости наклонной ватерлинии, а ЦТ груза g переместится в положение g1. Перемещение груза можно представить как приложение к судну двух противоположно направленных вертикальных сил p = mg вточках g и g1. Эти силы создают пару сил на плече l sin θ, где l - длина линии подвеса от нока стрелы О до ЦТ груза g. Момент этой пары δ М = р l sin θ уменьшает первоначальный восстанавливающий момент судна MB=Phsinθ, действовавший до отрыва груза от настила трюма. Восстанавливающий момент судна с подвешенным грузом равен MВ1 = МВ - δМ = Р(h-pl/P)sinθ (2.35)
Из формулы (2.35) видно, что в момент отрыва поднимаемого груза от настила, т. е. в тот момент, когда он становится подвешенным грузом, метацентрическая высота изменяется на величину δh = -pl/P = -ml/Δ (2.36) Из сравнения формул (2.36) и (2.27) следует, что влияние на остойчивость судна подвешенного груза равносильно влиянию подъема груза по вертикали на расстояние l, т. е. мгновенного перемещения его ЦТ в точку подвеса. Таким образом, дальнейший подъем груза на шкентеле после отрыва его от настила уже не сказывается на остойчивости судна. Влияние свободной поверхности жидкого груза на начальную остойчивость судна. На каждом судне размещается значительное количество жидких грузов (топлива, воды, смазочного масла) в цистернах (танках). Для наливных транспортных судов (танкеров) жидкий груз является основным перевозимым грузом. Если жидкий груз заполняет цистерну полностью, т. е. цистерна запрессована, то для задач статики он ничем не отличается от любого твердого груза такой же массы. Однако если жидкий груз заполняет лишь часть цистерны и, следовательно, имеет свободную поверхность, то он получает возможность переливаться при наклонении судна. В результате этого изменяется форма объема жидкости в цистерне и перемещается ЦТ судна, что отражается на его остойчивости. Предположим, что в одном из отсеков судна, первоначально запрессованном, остался жидкий груз с удельным весом γж, который в прямом положении судна заполняет отсек до уровня вл, имея объем υ (рис. 2.15). Если мы наклоним мысленно судно на малый угол Θ, то свободная поверхность жидкости в отсеке также наклонится и займет положение в1л1, параллельное наклонной ватерлинии В1Л1, а ЦТ жидкости g переместится в новое положение g1. Вследствие малости угла θ можно считать, что перемещение ЦТ жидкости происходит по дуге круга радиусом l с центром в точке m0, в которой пересекаются линии действия силы веса жидкого груза до и после наклонения судна. Как и в случае подвешенного твердого груза, переливание жидкого груза можно представить как приложение к судну двух противоположно направленных вертикальных сил Р = γж υ. Эти силы создают, пару сил с плечом l sinθ, момент которой δМ = γжυ l sinθ уменьшает первоначальный восстанавливающий момент MB=Phsinθ. Таким образом, с учетом переливания жидкости в отсеке восстанавливающий момент судна равен MВ1 = Phsinθ - γжυlsinθ = P(h-γжυl/P) sinθ (2.37)
Рис. 2.15. Влияние свободной поверхности жидкого груза на начальную остойчивость судна Сравнивая рис. 2.1 и 2.15, видим, что точку m0 можно рассматривать как метацентр жидкости в цистерне. Соответственно отрезок l = m0g является ее метацентрическим радиусом и поэтому может быть определен формулой, аналогичной формуле (2.5): I = ix/υ, (2.38) где IХ - центральный момент инерции свободной поверхности жидкости в цистерне относительно продольной оси (параллельной координатной оси Ох). Подставив выражение (2.38) в формулу (2.37), получим MВ1 = P(h-γж ix /P) sinθ (2.39) Как видно из уравнения (2.39), изменение начальной метацентрической высоты, отражающее переливание жидкости, может быть выражено формулой δ h = -γж ix /Р = -ρж iх/Δ. (2.40) Из выражения (2.40) следует, что при расходовании жидкого груза из запрессованных цистерн и появлении свободной поверхности всегда уменьшается остойчивость судна и что уменьшение метацентрической высоты не зависит от количества жидкого груза, поскольку в выражение для поправки δh не входит его объем υ. Если на судне расходуется с образованием свободных поверхностей несколько жидких грузов в отдельных, не сообщающихся между собой цистернах, то в формулу (2.40) вместо произведения ρжiх следует подставить сумму При возникновении свободных поверхностей в большом числе цистерн отрицательное приращение δh может оказаться по абсолютному значению столь велико, что начальная поперечная остойчивость судна станет отрицательной. Поэтому во избежание потери начальной остойчивости недопустимо одновременно расходовать жидкий груз из большого числа запрессованных цистерн (или принимать его одновременно в несколько порожних цистерн). Имеющиеся на судах Инструкции по приему и расходованию жидких грузов устанавливают определенный порядок расходования жидких грузов каждого вида (топлива, воды). Согласно этим инструкциям жидкость разрешается выкачивать из одной цистерны (или из одной пары цистерн правого и левого бортов) до полного их опорожнения, а затем переходить к расходованию из следующей цистерны и т. д. Прием жидких грузов производится в том же порядке, причем в каждую цистерну жидкость принимают до полной ее запрессовки. Следует иметь в виду, что если в цистерне имеется лишь очень тонкий слой жидкости, объем которой составляет менее 5 % объема цистерны (рис. 2.16, а), или цистерна заполнена почти доверху, т.е. объем жидкости составляет более 95 % объема цистерны (рис. 2.16, б), то ширина свободной поверхности bθ начинает резко уменьшаться после наклонения судна до некоторого весьма малого предельного угла крена θпред. Соответственно резкое уменьшение будет претерпевать и момент инерции свободной поверхности, а следовательно, и поправка к метацентрической высоте. В таких случаях говорят, что влияние свободной поверхности приводит к недейственной потере остойчивости, которую практически можно не учитывать при определении крена судна по метацентрической формуле.
Рис. 2.16. Случай недейственной потери остойчивости Появление свободной поверхности жидкого груза влияет также и на продольную остойчивость судна. Поправка к продольной метацентрической высоте будет определяться формулой δH = -ρжiу/Δ, (2.41) где iy - центральный момент инерции свободной поверхности жидкости относительно поперечной оси (параллельной координатной оси Оу). Однако ввиду значительной величины продольной метацентрической высоты H, превышающей примерно на два порядка величину поперечной метацентрической высоты, поправкой δH обычно пренебрегают. Влияние приема или снятия малого груза на посадку и начальную остойчивость судна. Будем считать сначала, как и ранее (при рассмотрении влияния перемещения груза), что в исходном равновесном положении судно сидит прямо и на ровный киль. Прием на судно малого груза в произвольную точку с координатами х, у, z (подразумеваются координаты ЦТ груза) можно рассматривать как процесс, слагающийся из двух последовательных операций: приема груза в точку с координатами Xf, Уf = О, z, т. е. в точку, расположенную на одной вертикали с ЦТ площади ватерлинии; переноса груза по горизонтали в заданную точку с координатами х, у. После выполнения первой операции судно сохранит свою первоначальную посадку прямо и на ровный киль; изменятся только его осадка и остойчивость (если сохранить по-прежнему допущение, что ввиду малости груза борта судна могут быть приняты вертикальными в пределах изменения осадки). После выполнения второй операции возникают моменты переноса ру и p (x - xf), которые приводят к образованию крена и дифферента судна. Углы крена и дифферента могут быть найдены по метацентрическим формулам
 
где h1 = h + δh и H1 = H+ δ H - начальные метацентрические высоты судна после приема груза; m - масса принятого груза; Δ - водоизмещение судна до приема груза. Для определения приращений высот δh и δH рассмотрим прием малого груза массой m, ЦТ которого располагается на одной вертикали с ЦТ площади ватерлинии в точке с аппликатой z (рис. 2.17). В результате увеличения осадки объемное водоизмещение судна увеличится на δV = m/ρ и возникнет дополнительная сила плавучести γδV, приложенная в ЦТ слоя между ватерлиниями ВЛ и В1Л1. В силу принятого допущения о прямобортности судна аппликата ЦТ дополнительного слоя плавучести будет равна d + δd/2, где приращение осадки δd определится формулами (1.21) или (1.22).
Наклоним мысленно судно на малый угол Θ, тогда сила веса груза p и равная ей дополнительная сила плавучести γδV составят пару сил с плечом (d + δd/2 - z) sin θ. Момент этой пары δM = p(d + δd/2 - z) sin θ увеличивает первоначальный восстанавливающий момент судна MB = Ph sin θ, поэтому восстанавливающий момент после приема груза становится равным МВ1 = Мв + δM, или (P + p)(h + δh)sinθ = Phsinθ + p(d + δd/2-z)sin θ (2.43) Решив уравнение (2.43) относительно искомого приращения δh и полагая Ρ = Δg и p = mg, получим δh = [m/(Δ + m)](d + δ d/2 – z – h). (2.44) Приращение продольной метацентрической высоты может быть найдено аналогичным путем: ΔH = [m/Δ + m)](d+δd/2 – z – H) (2.45) В формуле (2.45) сумма первых трех членов в скобках относительно мала по сравнению с H. Поэтому практически можно пользоваться приближенной формулой:
ΔH = -pH/(P + p) = - mH/(Δ + m) (2.46) В этом случае вторая формула (2.42) после преобразований примет вид Ψ = m(x-xf)/ΔH (2.47) Для приращений коэффициентов остойчивости Δk = (P + p)(h+δh) – Ph; δK = (P + p)(H+δH) – PH (2.48) Нетрудно получить выражение δk = δK = p(d + δd/2 – z). (2.49) После определения приращений, а следовательно, и новых значений метацентрических высот можно найти углы крена и дифферента по формулам (2.42) и новые осадки носом и кормой по формулам (2.32), но с учетом изменения средней осадки δd, определяемого формулами (1.21) или (1.22):
dк1 = d + δd – (L/2 + xf) ψ. (2.50) Если груз снимается с судна, то его масса т во все полученные формулы должна быть подставлена со знаком минус. В тех случаях когда судно до приема или снятия груза имело начальные (малые) крен или дифферент, в числители первой формулы (2.42) и формулу (2.47) следует подставить алгебраические суммы моментов, возникающих в результате приема (снятия) груза, и моментов Ρhθ0 и ΡΗψ0, отвечающих начальным углам крена и дифферента. Выполнив это и полагая Ρ = Δg и p = mg, находим
При использовании введенного ранее понятия момента
Нейтральные плоскости Определим условия, при которых прием или снятие малого груза не вызывает изменения коэффициентов остойчивости и начальных метацентрических высот - измерителей остойчивости. Последовательно приравняв нулю выражения (2.44), (2.45) и (2.49) и решив полученные уравнения относительно аппликаты ЦТ груза z, найдем, что начальные метацентрические высоты сохраняют свои значения при следующих условиях: поперечная метацентрическая высота при z = d + δd/2 – h, (2.53) продольная метацентрическая высота при z = d + δd/2 – H, (2.54) а коэффициенты остойчивости k и К сохраняют свои значения при z = d + δd/2 (2.55) Полученные выражения представляют собой уравнения так называемых нейтральных плоскостей, параллельных ОП. Если аппликата ЦТ груза удовлетворяет одному из этих уравнений, то его прием или снятие не вызывает изменения соответствующего данной нейтральной плоскости измерителя остойчивости. Исследуя выражения для приращений измерителей остойчивости, можно также прийти к выводу, что прием груза ниже нейтральной плоскости вызывает увеличение, а прием выше нее - уменьшение значений измерителей остойчивости. В случае снятия груза выводы будут противоположными, т. е. соответствующий измеритель остойчивости будет увеличиваться при снятии груза выше нейтральной плоскости и уменьшаться при снятии груза ниже нее. Знак приращения осадки δd зависит от того, принимается данный груз на судно или снимается с него. Следовательно, для каждого измерителя остойчивости имеются две нейтральные плоскости: одна для приема и другая для снятия груза, причем положение каждой плоскости по высоте зависит от массы принимаемого или снимаемого груза. Выражения (2.53) - (2.55) показывают, что у прямобортного судна нейтральные плоскости, относящиеся к различным измерителям остойчивости, располагаются следующим образом: для коэффициентов остойчивости и начальной поперечной метацентрической высоты несколько выше или ниже ватерлинии судна (практически можно считать, что они совпадают с плоскостью ватерлинии); для начальной продольной метацентрической высоты глубоко под килем судна. Следовательно, прием груза на судно всегда уменьшает, а снятие груза увеличивает начальную продольную метацентрическую высоту (но не продольную остойчивость как способность сопротивляться дифферен-тующим моментам, определяемую абсолютным измерителем - коэффициентом продольной остойчивости).
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 2666; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.011 с.) |

 Рис. 2.10. Разложение перемещения груза по координатным осям
Рис. 2.10. Разложение перемещения груза по координатным осям Рис. 2.11. Вертикальный перенос груза
Рис. 2.11. Вертикальный перенос груза
 1, т. е.
1, т. е. (2.30)
(2.30) (2.31)
(2.31)





 Рис. 2.14. Подвешенный груз
Рис. 2.14. Подвешенный груз
 где n - число отсеков с жидким грузом.
где n - число отсеков с жидким грузом.

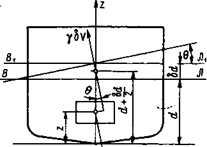 Рис. 2.17. Приеммалого груза
Рис. 2.17. Приеммалого груза dн1 = d + δd + (L/2 – xf) ψ;
dн1 = d + δd + (L/2 – xf) ψ;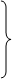

 (2.51)
(2.51)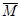 , дифферентующего на 1 м, для дифферента судна после приема или снятия малого груза получаем следующее выражение:
, дифферентующего на 1 м, для дифферента судна после приема или снятия малого груза получаем следующее выражение: (2.52)
(2.52)


