
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Начальная остойчивость суднаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Глава 1 ПЛАВУЧЕСТЬ СУДНА Геометрия корпуса судна Общее представление о форме корпуса. Корпус судна представляет собой удлиненное тело, которому обычно придается удобообтекаемая форма с целью уменьшения сопротивления воды и воздуха его движению. Для общей характеристики формы корпуса служат: формы сечений корпуса тремя взаимно перпендикулярными плоскостями; соотношения главных размерений корпуса; безразмерные коэффициенты полноты. В качестве трех взаимно перпендикулярных секущих плоскостей принимают (рис. 1.1): вертикальную продольную плоскость, проходящую посередине ширины судна и называемую диаметральной плоскостью (ДП); вертикальную поперечную плоскость, проходящую посередине расчетной длины судна и называемую плоскостью мидель-шпангоута (обозначается знаком ¤); горизонтальную плоскость, совпадающую с поверхностью воды и называемую плоскостью грузовой ватерлинии (плоскостью ГВЛ).
Рис. 1.1. Сечения корпуса судна и главные размерения
При проектировании судов, в частности судов, не предназначенных для перевозки грузов, иногда вместо ГВЛ, отвечающей осадке судна с полным грузом, пользуются некоторой условной ватерлинией - конструктивной ватерлинией (КВЛ). Диаметральная плоскость делит корпус судна на две симметричные части. Относительно плоскости мидель-шпангоута корпус судна, как правило, несимметричен, что обусловливается общепроектными соображениями и требованиями, связанными с обеспечением мореходных качеств судна. Плоскость ватерлинии делит корпус судна на две несимметричные части: подводную и надводную. У морских судов верхняя палуба, как правило, имеет седловатостъ, т. е. палубная линия в ДП является плавной кривой с подъемом от средней части судна в нос и в корму. Седловатость уменьшает заливаемость оконечностей и улучшает, таким образом мореходность судна. Чтобы обеспечить сток воды за борт, палубе в поперечном направлении придают обычно кривизну, называемую погибью. Диаметральная плоскость и плоскость мидель-шпангоута являются главными координатными плоскостями, используемыми при решении задач статики судна. Третьей координатной плоскостью является основная плоскость (ОП), параллельная плоскости ватерлинии и проходящая через линию пересечения верхней кромки горизонтального киля с плоскостью мидель-шпангоута. Главные размерения судна и их соотношения. Главными размерениями судна являются (см. рис. 1.1): расчетная длина судна L; различают две расчетные длины, используемые при решении задач статики судна: длину по КВЛ Lквл измеряемую вдоль следа КВЛ на ДП между точками пересечения КВЛ с передней кромкой форштевня и очертанием кормы по внутренней поверхности наружной обшивки; длину между перпендикулярами L┴┴, измеряемую в ДП между перпендикулярами к ОП, проведенными через точки пересечения КВЛ с передней кромкой форштевня [носовым перпендикуляром (НП)] и с осью баллера руля [ кормовым перпендикуляром (КП)]; расчетная ширина судна В, измеряемая на уровне плоскости КВЛ в наиболее широком ее месте между внутренними поверхностями наружной обшивки; высота борта D, измеряемая в плоскости мидель-шпангоута по вертикали у борта от ОП до линии пересечения внутренней поверхности бортовой обшивки с нижней поверхностью палубного настила верхней водонепроницаемой палубы; осадка судна d, измеряемая в плоскости мидель-шпангоута по вертикали от ОП до уровня ГВЛ. Разность между высотой борта D и осадкой d определяет высоту надводного борта F. Все перечисленные главные размерения носят название расчетных, или теоретических, так как они не учитывают толщины наружной обшивки корпуса. Теоретические главные размерения используют в различных расчетах, выполняемых для оценки качеств судна, определяемых его геометрической формой. Для общей характеристики формы корпуса служат следующие соотношения главных размерений: отношение L/B, определяющее в значительной степени ходовые качества судна; отношение B/d, влияющее на остойчивость, качку и ходовые качества; отношение L/D, влияющее на прочность судна; отношение D/d, определяющее остойчивость на больших углах крена и непотопляемость судна. Безразмерные коэффициенты, полноты. Кроме указанных выше отношений главных размерений для характеристики формы подводной части судна используют безразмерные коэффициенты полноты: коэффициент полноты площади КВЛ - отношение площади ватерлинии S к площади прямоугольника со сторонами L и В: α=S/(LB); (1.1) коэффициент полноты площади мидель-шпангоута - отношение площади подводной части мидель-шпангоута ω к площади прямоугольника со сторонами В и d: β = ω/(Bd); (1.2) коэффициент общей полноты - отношение объема подводной части, или объемного водоизмещения, судна V к объему параллелепипеда со сторонами L, В и d: Cb = V/(LBd); (1.3) коэффициент продольной полноты - отношение объемного водоизмещения судна V к объему цилиндра, имеющего основанием площадь мидель-шпангоута ω и высоту L: φ = V/(ωL); (1.4) коэффициент вертикальной полноты - отношение объемного водоизмещения судна V к объему цилиндра, имеющего основанием площадь КВЛ S и высоту d: χ = V/(Sd). (1.5) Коэффициенты α, β и Сb считаются основными независимыми коэффициентами, а коэффициенты φ и χ - производными от них, связанными соотношениями φ=Cb/β; Х=Сb/α. (1.6) Координатные оси и параметры посадки судна. Положение судна относительно невозмущенной поверхности воды называют его посадкой. В задачах, связанных с определением посадки судна, обычно используют связанную с судном прямоугольную координатную систему Oxyz, в которой ось Ох направлена в нос по линии пересечения ДП с ОП, ось Оу - на правый борт по линии пересечения плоскости мидель-шпангоута с ОП, ось Oz - вверх по линии пересечения ДП с плоскостью мидель-шпангоута (рис. 1.2).
В общем случае посадка судна, а следовательно, и положение его ватерлинии в указанной выше координатной системе определяются тремя параметрами, в качестве которых принимают среднюю осадку d- аппликату точки пересечения плоскости ватерлинии с осью Oz; угол θ - угол между осью Оу и линией пересечения плоскости ватерлинии с плоскостью мидель-шпангоута (миделевым следом ватерлинии); угол ψ - угол между осью Ох и линией пересечения плоскости ватерлинии с ДП (диаметральным следом ватерлинии). Если θ = 0, то говорят, что судно сидит прямо; если ψ = 0, то говорят, что судно сидит на ровный киль. Обычно параметр θ называют углом крена, а параметр ψ - углом дифферента, хотя, строго говоря, угол θ является углом крена только при ψ = 0, а угол ψ - углом дифферента только при θ = 0. Положительными направлениями отсчета углов считают: для θ - направление от оси Оу по часовой стрелке, если смотреть с положительного конца оси Ох, а для ψ - направление от оси Ох против часовой стрелки, если смотреть с положительного конца оси Оу. Таким образом, положительными будут дифферент на нос и крен на правый борт. Если судно сидит прямо (θ = 0), то его посадка может быть определена двумя параметрами d и ψ или значениями осадок носом и кормой (на НП и КП): Dн = d + L/2 tg ψ ~ d + L/2 ψ (1.7) Dк = d - L/2 tg ψ ~ d - L/2 ψ (1.8) Разность осадок носом и кормой dH - dK называют дифферентом судна. Угол дифферента и дифферент связаны следующей зависимостью: dн - dк = L · tg ψ ≈ L·ψ. (1.9) Теоретический чертеж судна. Соотношения главных размерений и коэффициенты полноты не могут дать точного представления о форме корпуса судна: при одних и тех же значениях главных размерений, их соотношений и коэффициентов полноты можно получить множество отличных друг от друга форм корпуса. Точное представление о форме корпуса судна может дать только его теоретический чертеж (рис. 1.3), необходимый для расчетов плавучести, остойчивости, непотопляемости; разработки чертежей общего расположения судна и конструктивных чертежей корпуса. На теоретическом чертеже стального судна изображают теоретическую поверхность корпуса без наружной обшивки, толщина которой мала по сравнению с размерами судна, в проекциях на три взаимно перпендикулярные координатные плоскости: ДП, плоскость мидель-шпангоута и ОП. Эти проекции называют соответственно „Боком", „Корпусом" и „Полуширотой". Метод изображения корпуса судна на теоретическом чертеже заключается в вычерчивании совокупности сечений его поверхности рядом плоскостей, параллельных указанным трем плоскостям проекций. Сечения теоретической поверхности судна вертикальными плоскостями, параллельными ДП, называют батоксами; сечения вертикальными плоскостями, параллельными плоскости мидель-шпангоута, - теоретическими шпангоутами; сечения горизонтальными плоскостями, параллельными ОП, - ватерлиниями. Каждое сечение проецируется на одну из плоскостей в своем истинном виде, а на две другие плоскости - в виде прямых линий. Например, каждая ватерлиния изображается в своем истинном виде на „Полушироте" и в виде прямых линий на „Корпусе" и „Боку". Поскольку корпус судна симметричен относительно ДП, на „Полушироте" вычерчивают только половины ватерлиний, а на „Корпусе" - половины шпангоутов; при этом половины носовых шпангоутов изображают справа, а кормовых - слева от следа ДП. Нос судна на „Полушироте" и „Боку" в отечественной практике принято располагать справа. Все три проекции корпуса судна на теоретическом чертеже представляют одну и ту же поверхность, поэтому координаты всех точек пересечения шпангоутов, ватерлиний и батоксов должны быть согласованы на всех проекциях. Все однотипные сечения обычно проводят на равных расстояниях. Число равноотстоящих от ГВЛ ватерлиний зависит от требуемой точности расчетов теоретических элементов судна. Ватерлинии нумеруют по порядку снизу вверх (ОП рассматривают как нулевую ватерлинию). Выше ГВЛ также проводят несколько ватерлиний, чтобы обеспечить необходимое согласование плавности обводов в надводной части судна. Число равноотстоящих теоретических шпангоутов, включая НП и КП, принимают обычно равным 21, т. е. расчетную длину судна делят на 20 равных частей, именуемых теоретическими шпациями. Плавучесть судна Плавучестью называют способность судна поддерживать вертикальное равновесие в заданном положении относительно поверхности воды в результате действия силы веса судна и выталкивающей силы воды. Свойство плавучести отличает судно от других инженерных сооружений. Мерой плавучести судна является его водоизмещение Δ = ρ·V. где ρ - плотность забортной воды.
Условия и уравнения равновесия плавающего судна. На судно, плавающее неподвижно в положении равновесия на спокойной поверхности воды, действуют следующие силы (рис. 1.4): - сила веса всех его частей, которые приводятся к их равнодействующей - силе веса судна Ρ = δg, направленной вертикально вниз и приложенной в центре тяжести (ЦТ) судна G (xg, yg, zg); - гидростатические силы давления воды, действующие по нормалям к подводной поверхности судна; горизонтальные составляющие этих сил взаимно уравновешиваются, а вертикальные составляющие приводятся к их равнодействующей - силе плавучести γ·V (γ - удельный вес забортной воды), направленной вертикально вверх и приложенной в центре величины (ЦВ)- ЦТ подводного объема судна С (хс, ус, zc). На корпус движущегося судна действуют, кроме того, гидродинамические силы давления воды, имеющие также не только горизонтальные, но и вертикальные составляющие. Однако при решении большинства задач статики судна подъемной силой корпуса, обусловленной гидродинамическими силами давления воды, пренебрегают. Эти силы учитывают только в некоторых специальных задачах статики, например в задачах, связанных с остойчивостью глиссирующих судов. Основным физическим законом, определяющим плавучесть судна, служит закон Архимеда, согласно которому сила веса судна равна силе плавучести, а масса (водоизмещение судна Δ) равна массе вытесненной им воды: P = γ · V; Δ = ρ · V (1.10) Формулы (1.10) являются математическими выражениями первого условия равновесия плавающего судна. Из теоретической механики известно, что для равенства двух сил необходимо и достаточно, чтобы они были равны по абсолютной величине и направлены противоположно друг другу по прямой, соединяющей точки их приложения. В данном случае обе силы - сила веса и сила плавучести - направлены вертикально; следовательно, вторым условием равновесия плавающего судна является расположение точек приложения этих сил - ЦТ и ЦВ - на одной вертикали, т. е. на одном перпендикуляре к плоскости ватерлинии. Уравнение плоскости ватерлинии может быть записано в виде x · tgψ + y · tgθ - z + d = 0. (1.11) Из аналитической геометрии известно, что прямая, соединяющая точки G и С, будет перпендикулярна плоскости, выраженной уравнением (1.11), в том случае, когда удовлетворяются следующие уравнения:
(yg-yc) + (zg-zc)tgθ = 0. (1.12) Уравнения (1.12) выражают второе условие равновесия плaвaющeго судна. В совокупности уравнения (1.10) и (1.12) называют системой уравнений равновесия судна. Если судно сидит прямо и на ровный киль (θ = ψ = 0), то уравнения равновесия (1.12) принимают вид xg=xc; yg=yc. (1.13) Определение массы и координат ЦТ судна. Для использования уравнений равновесия при решении практических задач статики судна необходимо уметь определять массу судна и координаты его ЦТ при любом заданном состоянии его нагрузки. В этом случае масса судна (его водоизмещение Δ) складывается из масс порожнего судна, команды, снабжения, судовых запасов и балласта, а также перевозимых грузов и пассажиров с багажом. В целях систематизации учета масс и расчета координат ЦТ судна составляют таблицу нагрузки судна (табл. 1.1), в которую заносят массы всех элементов (статей) нагрузки mi, координаты (плечи) их ЦТ xi иzi, а также статические моменты mixi и mizi относительно соответствующих координатных плоскостей. При заполнении таблицы используют судовую документацию (чертежи общего расположения, таблицы элементов топливных и других цистерн, чертеж размещения грузов и др.).
Таблица 1.1. Таблица нагрузки судна
После суммирования по графам 2, 4 и 6 таблицы нагрузки судна находят Δ = Σmi ; xg = Σmixi / Σmi; zg = Σmizi / Σmi (1.14) Поскольку подводный объем судна симметричен относительно ДП, то определять ординату ЦТ yg нет необходимости, так как она должна быть равна или близка нулю. В противном случае судно получит крен, наличие которого в эксплуатационных условиях недопустимо. Разность между массой судна с полным грузом и массой порожнего судна носит название дедвейта судна. Таким образом, в дедвейт судна входят массы команды и пассажиров с багажом, провизии, расходных материалов, судовых запасов, полезного груза в трюмах судна и постоянного водяного балласта (если таковой предусматривается). Массы всех грузов и пассажиров с багажом, перевозка которых является назначением судна, составляет полезную, или чистую, грузоподъемность судна. Для определения координат ЦТ однородного генерального или насыпного груза в грузовых помещениях (трюмах и твиндеках) служит чертеж размещения грузов на судне, представляющий собой продольный разрез судна, вычерчиваемый в искаженном (сжатом по длине) масштабе. На каждом грузовом помещении, изображенном на этом чертеже (рис. 1.5), наносят кривую с двумя шкалами - шкалой объемов генерального груза в данном помещении при данном уровне его заполнения и шкалой аппликат его ЦТ. Кроме того, в нижней части чертежа наносят горизонтальную шкалу, позволяющую определить абсциссу ЦТ груза. Определение теоретических элементов корпуса судна в судовых условиях. В конструкторских бюро при проектировании судна теоретические элементы корпуса судна (в предположении его посадки прямо и на ровный киль) вычисляют в зависимости от осадки судна по стандартной методике с использованием ЭВМ и ординат теоретического чертежа. Результаты таких расчетов позволяют построить ряд кривых, с помощью которых определяют в судовых условиях теоретические элементы, используемые при решении различных практических задач статики судна, К числу таких элементов относятся: водоизмещение Δ и объемное водоизмещение V; координаты ЦВ хс и zc; площадь ватерлинии S; абсцисса ЦТ площади ватерлинии xf; коэффициент общей полноты Cb; коэффициенты полноты площади ватерлинии α и площади мидель-шпангоута β; центральные моменты инерции площади ватерлинии 1x и Iyf;аппликаты поперечного и продольного метацентров zm и zm; поперечный и продольный метацентрические радиусы r и R, момент
Совокупность кривых, выражающих графически зависимость перечисленных элементов от осадки судна, изображают на одном чертеже, который носит название кривые элементов теоретического чертежа (рис. 1.6).
На этом чертеже ординаты кривых хс и xf откладывают от вертикали, представляющей собой след плоскости мидель-шпангоута на ДП, а ординаты прочих кривых - от некоторых условных вертикалей, причем масштаб ординат указывают на самих кривых или же на шкалах, вычерчиваемых в нижней и верхней частях чертежа. Указанный чертеж выдается на судно в составе отчетной документации; он позволяет быстро и без каких-либо вычислений находить значения всех требуемых теоретических элементов корпуса судна для любой осадки. Кривая водоизмещения и грузовой размер. Кривую, выражающую зависимость объемного водоизмещения судна V от его осадки, называют кривой водоизмещения. Если же ординаты кривой водоизмещения умножить на расчетную плотность забортной воды (обычно принимают ρ = 1,025 т/м3), то получим кривую Δ =f(d), именуемую грузовым размером (рис. 1.7).
Наряду с кривой водоизмещения и грузовым размером на судне пользуются грузовой шкалой (рис. 1.8), также выражающей зависимость V и Δ от осадки судна.
Строевая по ватерлиниям. Кривую, выражающую зависимость площади ватерлинии S от осадки судна d, называют строевой по ватерлиниям (рис. 1.9). Строевая по ватерлиниям обладает следующими свойствами: - площадь строевой, ограниченная заданной ватерлинией, с учетом масштаба численно равна объемному водоизмещению судна при данной осадке; - ордината ЦТ А площади строевой с учетом масштаба равна аппликате zc ЦВ судна при данной осадке; - коэффициент полноты площади строевой равен коэффициенту вертикальной полноты судна χ при данной осадке.
Масштаб Бонжана. Как было указано выше, кривую водоизмещения, как и прочие кривые элементов теоретического чертежа, строят для посадки судна на ровный киль, поэтому, если судно имеет значительный дифферент, то использование этой кривой может привести к значительной погрешности вычислений. Для более точного определения объемного водоизмещения, а также абсциссы ЦВ в случае посадки судна прямо, но с дифферентом служит специальная диаграмма, называемая масштабом Бонжана.
Масштаб Бонжана представляет собой совокупность кривых, каждая из которых определяет в некотором масштабе погруженную площадь теоретического шпангоута в зависимости от его углубления, и строится от следа соответствующего шпангоута на ДП (рис. 1.10). Как и теоретический чертеж судна, масштаб Бонжана строится для 21 теоретического шпангоута, т. е. расчетная длина судна (между перпендикулярами) делится на 20 равных частей. На рис. 1.10 для упрощения кривые погруженных площадей показаны только для четных шпангоутов (0-, 2-, 4-го и т. д.). С целью сокращения длины масштаб Бонжана строят в искаженном виде, например в масштабах 1: 100 по длине, 1: 25 по высоте. Чтобы использовать масштаб Бонжана, необходимо прежде всего нанести на него ватерлинию судна. Для этого замеряют с плотика или шлюпки осадки судна dн.м и dк.м по носовым и кормовым маркам углубления и откладывают эти осадки на соответствующих вертикалях, обычно не совпадающих с НП и КП и отстоящих от последних соответственно на расстояниях l н и l к. Полученные точки Аи В соединяют прямой линией. Для повышения точности замера осадок при наличии небольшого волнения рекомендуется применять открытую с обоих концов стеклянную трубку длиной около 0,5 м. При небольших колебаниях поверхности воды в районе марок углубления уровень воды в трубке будет оставаться практически неподвижным. Следует иметь в виду также, что марки углубления наносят от нижней кромки горизонтального киля, толщина которого должна быть учтена при нанесении на чертеж точек Аи В. Далее снимают с кривых погруженные площади шпангоутов ω так, как показано на рис. 1.10 для 8-го шпангоута. После этого определяют объемное водоизмещение и абсциссу ЦВ судна путем табличного вычисления интегралов по правилу трапеций:
Рабочая форма вычисления этих интегралов приведена в табл. 1.2. Таблица 1.2. Рабочая форма вычисления Vи хс
Примечание. l = L/20 — расстояние между шпангоутами. Как правило, в результате неравномерного распределения грузов по длине корпус судна имеет прогиб или перегиб, максимальная стрелка которого даже на тихой воде может достигать 0,2- 0,3м. В этом случае ватерлиния на масштабе Бонжана будет иметь вид пологой кривой AЕВ (см. рис. 1.10, где показан случай перегиба корпуса, когда фактическая осадка на миделе меньше теоретической средней осадки). С достаточной для практических целей точностью можно принять, что максимальной стрелка прогиба (перегиба) будет в плоскости мидель-шпангоута, а поправку к водоизмещению выразить формулой
где f - максимальная стрелка прогиба (перегиба) корпуса. Как видно из рис. 1.10, стрелка прогиба в плоскости мидель-шпангоута определяется следующим выражением: f = D + tп - Fл – m - dcp. (1.17) Здесь D - теоретическая высота борта судна; tn - толщина палубного стрингера; Fл - назначенная судну высота летнего надводного борта; m - измеренное по борту расстояние от летней ГВЛ до уровня воды в плоскости мидель-шпангоута; dcp - средняя теоретическая осадка (при отсутствии деформации корпуса), равная
где tκ - толщина горизонтального киля. Масштаб Бонжана обычно строят без учета выступающих частей, объем которых (необходимый для уточнения водоизмещения) и продольный статический момент (необходимый для уточнения xc) должны быть определены особым расчетом. Строевая по шпангоутам. Кривую, выражающую закон распределения погруженных площадей шпангоутов по длине судна, называют строевой по шпангоутам. С помощью масштаба Бонжана эта кривая, ординаты которой в некотором масштабе численно равны погруженным площадям шпангоутов, может быть построена для любой ватерлинии судна, сидящего как на ровный киль, так и с дифферентом (рис. 1.11). Строевая по шпангоутам обладает следующими свойствами: - площадь, ограниченная строевой, численно равна с учетом масштаба объемному водоизмещению судна; - абсцисса ЦТ площади строевой равна с учетом масштаба абсциссе ЦВ судна; - коэффициент полноты площади строевой равен коэффициенту φ продольной полноты судна. Изменение осадки судна от приема или снятия малого груза. В результате приема на судно малого груза массой т в точку с координатами х, у (рис. 1.12) возникнет сила веса груза ρ = mg и посадка судна изменится: увеличится его средняя осадка и в общем случае возникнут крен и дифферент. Предположим, однако, что судно удерживается от крена и дифферента некоторым условным (воображаемым) внешним моментом и рассмотрим здесь только изменение осадки судна δd. В результате увеличения осадки в воду войдет дополнительный объем δV между ватерлиниями ВЛ и В1Л1и возникнет дополнительная сила плавучести γδV, приложенная в ЦТ этого объема и равная силе веса груза р. Поскольку предполагается, что масса груза мала по сравнению с массой судна, то можно считать, что борта судна в пределах изменения осадки вертикальны. В этом случае вошедший в воду объем δV можно определить как объем цилиндрического тела, основанием которого служит площадь ватерлинии S, а высотой - искомое приращение осадки δd δV = Sδd. (1.19)
Рис. 1.11. Строевая по шпангоутам Рис. 1.12. Изменение осадки судна при приеме малого груза
Для определения приращения осадки δd используем условие равновесия судна после приема груза, выражающееся равенством дополнительных сил веса и плавучести p = γδν. (1.20) Подставив выражение (1.20) в уравнение (1.19) и решив последнее относительно δd, получим δd = p/(γS) = m/(ρS). (1.21) Если груз снимается с судна, то его массу т подставляют в формулу (1.21) с отрицательным знаком; следовательно, приращение осадки в этом случае будет также отрицательным, т. е. осадка судна уменьшится на величину δd. На рис. 1.12 видно, что в общем случае силы pи γδV составляют пару сил, момент которой вызовет крен и дифферент свободно плавающего судна. Этот момент будет равен нулю только в том случае, если эти силы будут действовать по одной вертикали. При допущении о прямобортности судна в пределах изменения осадки ЦТ объема δV будет расположен на одной вертикали с ЦТ площади ватерлинии ВЛ. Следовательно, при приеме или снятии груза судно нe получит крена или дифферента, если ЦТ принятого (снятого) груза будет расположен на одной вертикали с ЦТ площади ватерлинии. Положение груза, отвечающее этому условию, показано на рис. 1.12 штриховой линией. Формула (1.21) является точной для прямобортного судна и приближенной для непрямобортного. В последнем случае она определяет приращение осадки с достаточной для практических целей точностью, если масса принимаемого или снимаемого груза не превышает 15-20 % массы судна. В практических расчетах часто используют также величину q - число тонн на 1см осадки. Если известно q, то приращение осадки выразится формулой δd = m/q. (1.22) Сравнивая формулы (1.21) и (1.22), видим, что величина q пропорциональна площади ватерлинии S и связана с ней зависимостью q = ρS/100. (1.23) Зная площади ватерлиний при различных осадках и принимая среднюю (расчетную) плотность морской воды ρ равной 1,025 т/м3, с помощью этой формулы можно построить кривую q= f (d). Однако при наличии строевой по ватерлинии строить такую кривую нет надобности, так как достаточно снабдить строевую по ватерлиниям дополнительной шкалой для q. Изменение осадки от приема или снятия большого груза. Если масса принимаемого на судно или снимаемого с судна груза превышает 15- 20 % массы самого судна, то формулы (1.21) и (1.22) не обеспечивают необходимой точности расчета. В таких случаях изменение осадки определяют графически, пользуясь грузовым размером Δ = f (d). Пусть начальное водоизмещение судна (до приема груза) равно Δ0, а соответствующая ему осадка - d0 (рис. 1.13). Отложим значение массы принятого груза т в масштабе оси абсцисс вправо от точки Δ0 и через полученную точку проведем вертикаль. Точку В пересечения этой вертикали с грузовым размером снесем по горизонтали на ось ординат, где по шкале d найдем новую осадку судна, а следовательно, и приращение осадки δd. В случае снятия груза его массу откладывают по оси абсцисс не вправо, а влево от точки, отвечающей первоначальному водоизмещению Δ0.
Изменение осадки при перемене плотности воды. Плотность забортной воды зависит главным образом от ее солености, а также от температуры. В ряде случаев морские транспортные суда принимают груз в портах с пресной водой, т. е. при ρ = 1,0 т/м3, и их осадка уменьшается после выхода в открытое море, где плотность воды может составлять 1,015-1,035т/м3. Наибольшая допустимая осадка судна в морской воде задается Правилами о грузовой марке морских судов, поэтому для максимального использования грузоподъемности судна при его погрузке в пресной воде необходимо оценить уменьшение осадки при переходе из пресной воды в морскую. Для решения этой задачи в самом общем случае предположим, что судно, имеющее объемное водоизмещение V в воде с плотностью ρ 1, переходит в воду с плотностью ρ2, вследствие чего его объемное водоизмещение получает приращение δV. Масса судна при этом не изменяется, следовательно, ριV=ρ2(V+δV). (1.24) Поскольку искомое изменение осадки δd относительно невелико (по сравнению с самой осадкой), то можно принять δV = Sδd, где S-площадь ватерлинии судна. Таким oбрaзoм, уравнение (1.24) принимает вид ρ1V = ρ2(V + S δ d). (1.25), Решив это уравнение относительно δd, получим δd = (V/S)(ρ 1- ρ2)/ ρ2. (1.26) Подставляя в формулу (1.26) среднее (расчетное) значение плотности морской воды ρ 1 = l,025т/м3 и принимая для пресной воды ρ 2 = 1,0 т/м3, а также подставляя S=100q/ρ согласно формуле (1.23), получаем δd = (l/40)Δ/(100q), (1.27) или, выражая δd в сантиметрах, δd = Δ /(40q). (1.28) Таким образом, осадка судна увеличивается на величину, определяемую формулой (1.28), при переходе из морской воды в пресную и уменьшается на ту же величину при переходе из пресной воды в морскую. Запас плавучести и грузовые марки. Запасом плавучести называют непроницаемый для воды объем корпуса судна, расположенный выше ГВЛ и включающий помещения, ограниченные верхней водонепроницаемой палубой, а также водонепроницаемые надстройки и рубки. Он определяет дополнительную нагрузку, которую может принять судно до того, как оно потеряет способность держаться на воде. Запас плавучести, выраженный в процентах от объемного водоизмещения судна, на транспортных грузовых судах составляет 25-30 %, на танкерах 10-15, на пассажирских судах 80-100 %. Необходимый запас плавучести судна обеспечивается назначением ему минимальной высоты надводного борта, достаточной для безопасного плавания в определенных районах и в определенное время года. Судам, плавающим под флагом СССР, минимальный надводный борт устанавливается согласно Правилам о грузовой марке морских судов, разработанным Регистром СССР на основе Международной конвенции о грузовой марке. В Правилах изложена методика назначения минимального надводного борта в зависимости от длины судна, коэффициента общей полноты, расчетной длины надстроек, седловатости палубы, погиби бимсов и других параметров. Необходимым условием для возможности использования этой методики является удовлетворение содержащихся в Правилах требований к прочности и остойчивости судна и действий его личного состава в море (закрытий отверстий в корпусе, ограждений и др.). Назначенную судну высоту надводного борта наносят белой или желтой краской на темном фоне или черной краской на светлом фоне на обоих бортах судна в виде грузовой марки, состоящей из трех частей: отметки палубной линии, знака грузовой марки и грузовых марок, указывающих наибольшие осадки, до которых судно может быть нагружено при различных условиях плавания. Палубная линия. На каждом борту судна наносят горизонтальную палубную линию длиной 300 мм, середина которой располагается в плоскости мидель-шпангоута. Верхнюю кромку палубной линии проводят по линии пересечения продолженной наружу верхней поверхности палубы надводного борта с наружной поверхностью бортовой обшивки (рис. 1.14). Если на палубе имеется деревянный настил, то верхняя кромка палубной линии должна быть проведена по линии пересечения продолженной наружу верхней поверхности деревянного настила с наружной поверхностью бортовой обшивки. Знак грузовой марки. От верхней кромки палубной линии вертикально вн
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 1860; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.236.93 (0.015 с.) |

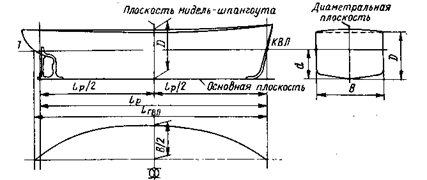
 Рис. 1.3. Теоретический чертеж судна
Рис. 1.3. Теоретический чертеж судна Рис. 1.4. Силы, действующие на плавающее судно
Рис. 1.4. Силы, действующие на плавающее судно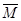 , дифферентующий на 1 м.
, дифферентующий на 1 м. Рис. 1.5. Кривая для определения объема и координат груза в трюме
Рис. 1.5. Кривая для определения объема и координат груза в трюме Рис. 1.6. Кривые элементов теоретического чертежа
Рис. 1.6. Кривые элементов теоретического чертежа Рис. 1.7. Грузовой размер
Рис. 1.7. Грузовой размер Рис. 1.8. Грузовая шкала
Рис. 1.8. Грузовая шкала Рис. 1.9. Строевая по ватерлиниям
Рис. 1.9. Строевая по ватерлиниям Рис. 1.10. Масштаб Бонжана
Рис. 1.10. Масштаб Бонжана
 (1.15)
(1.15) (1.16)
(1.16) (1.18)
(1.18)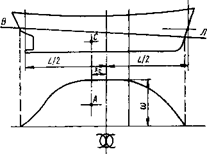
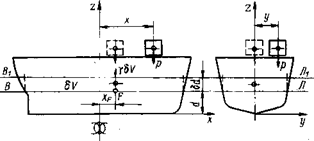
 Рис. 1.13. График изменения осадки судна при приеме или снятии большого груза
Рис. 1.13. График изменения осадки судна при приеме или снятии большого груза


