Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение уравнения ШредингераСодержание книги
Поиск на нашем сайте
Рассмотрим теперь качественно метод, используемый для решения уравнения Шредингера для случая атома водорода. Первым шагом является упрощение решения путем преобразования уравнения от декартовых координат (оси х, у и z) к сферическим полярным координатам. При преобразовании системы координат уравнение Шредингера переходит в уравнение
( . +( Здесь m — приведенная масса ' m = где М— масса ядра, m—масса электрона. Уравнение можно разделить на более простые уравнения, каждое из которых включает только одну переменную r, q или j и может быть решено независимо. Эти уравнения имеют бесконечное множество решений; но, для того чтобы решения имели смысл для описания поведения электрона в атоме, они должны удовлетворять изложенным ниже требованиям «а» — «в». Каждое возможное решение представляет собой волновую функцию y, описывающую орбиталь — состояние атома. Для выделения пригодных решений из бесконечного общего числа их нужно отобрать те, точки, что удовлетворяют следующим условиям: а) волновая функция должна быть конечной и непрерывной т. е. она не должна обращаться в бесконечность ни при каких значениях r, q и j. б) решение должно быть однозначным, т. е. в любой данной точке амплитуда может иметь только одно значение, а не несколько; в) решения должны быть нормированы; это условие требует, чтобы взятый по всему пространству интеграл от функции (являющейся решением), возведенной в квадрат и умноженной на dt, был равен единице, т. е.
Поскольку y2dt связано с вероятностью нахождения электрона в элементе объема dt, интегрирование в уравнении просто требует, чтобы вероятность нахождения электрона где-либо в пространстве была равна единице. Для неионизованного атома имеется лишь ограниченное число решений уравнения Шрёдингера, удовлетворяющих всем сформулированным выше требованиям. Такие дозволенные решения называются собственными функциями, и каждое из них описывает состояние — орбиталь, на которой в атоме могут находиться два электрона Орбитали отличаются нижними индексами при y; каждая орбиталь однозначно определяется набором квантовых чисел n,l и m, где n соответствует основному номеру оболочки Уравнения для ynp разделяются на радиальную часть yr (зависящую от расстояния г) и угловую часть yqj (являющуюся функцией углов q и j). Полная волновая функция представляет собой просто произведение этих двух частей, т. е. y=yqjyr.Выражения для s-орбиталей не включают никакой зависимости от углов, и поэтому они обладают сферической симметрией. Число решений указывает, сколько существует орбиталей с данной энергией (т. е. в данной оболочке с одним главным квантовым числом). Для орбитали, отвечающей оболочке с n=1 (т.е. оболочке с самой низшей энергией), возможно только одно решение y1s. Для значений энергии, соответствующих n=2, имеются два очень близких энергетических уровня, соответствующих волновым функциям y2s и y2p. Есть только одно решение для y2s и три решения для y2p, соответствующие трем орбиталям y2p0,y2p+1,y2p-1. Эти три 2р-орбитали имеют все одинаковую энергию. Для описания равенства энергий трех орбиталей используется термин«триждывырожденные». Для энергий, отвечающих оболочке с п=3, имеется девять решений, соответствующих одной y3s-орбитали, трем вырожденным y3p-орбиталям и пяти вырожденным ysd-орбиталям. Решений, которые отвечали бы орбиталям y1p или y2d, нет, и таких орбиталей нет. Таким образом, выбрав в качестве модели стоячую волну, включив в волновое уравнение гипотезу де Бройля и отобрав физически приемлемые решения получившегося уравнения, можно сосчитать число возможных орбиталей в атоме водорода.
4.5 КВАНТОВЫЕ ЧИСЛА
n - главное (радиальное) l - орбитальное (азимутальное) ml = магнитное. - Существует ряд правил, которые позволяют определять возможные значения n, l и ml;. Квантовое число n может иметь любое положительное целочисленное значение, за исключением нуля. Все возможные значения l, соответствующие данному n, передаются соотношением l =п— 1 ,..., 0, где многоточие означает все целые числа, необходимые для заполнения ряда. Возможными значениями ml;, соответствующими данному l, являются ml;= +l, l—1,..., 0,.... —l+1, —l. На каждой орбитали могут находиться два электрона, которые отличаются квантовым числом спинового магнитного момента ms, равным либо +1/2,либо —1/2. Квантовые числа n,lи ml и приведенные выше правила являются следствием решения уравнения Шрёдингера.. Главное квантовое число n появляется при решении уравнения для радиальной части функции y и в первом приближении определят энергию орбитали. Главное квантовое число связано также качественно с расстоянием от ядра до наиболее вероятной области нахождения электрона. Это квантовое число соответствует оболочкам К, L, М и т. д. в модели Бора.
Квантовые числа l и mi появляются при решении уравнений для угловой части функции y и связаны соответственно с величиной и ориентацией углового момента (произведения угловой скорости на момент инерции) электрона на данной орбитали. Орбиталь с l=0 является сферической, не имеет углового момента и обозначается буквой s. Oбычно используются следующие символы: s для l==0, р для l=1, d для l = 2, f для l=3. S – sharp - резкий P – principal - главный d – diffuse – диффузный f – fundamental - основной . Спиновые квантовые числа ms, равные +1/2 или -1/2, не появляются при решении. уравнения Шрёдингера, но необходимы для того, чтобы однозначно описать состояние электронов в атоме. Это квантовое число ассоциировано со спиновым угловым моментом электрона (грубой физической моделью этого свойства может служить представление о вращении электрона вокруг своей оси). При описании орбитали обычно указывается главное квантовое число n и затем даются сокращенные обозначения орбитального квантового числа l в виде s, p, d или f, например 3p. Имеются три такие 3p-орбитали, соответствующие ml=+l, 0 и -1 Существование таких орбиталей подтверждается опытными данными, полученными из атомных спектров. Электронные переходы с одной орбитали на другую,(т. е. на уровень с другой энергией), сопровождаются поглощением (если электрон возбуждается на орбиталь с более высокой энергией) или испусканием (если электрон переходит на орбиталь с более низкой энергией) излучения, частота которого n связана с разностью энергий орбиталей выражением E=hn. Главные линии в атомных спектрах соответствуют большим разностям энергий и обусловлены электронными переходами между уровнями энергий с различными значениями n. Переходы между уровнями с одинаковыми n, но различными l (т. е. s, p, d, f), приводят к появлению тонкой структуры основных линий, так как разным значениям l соответствуют небольшие различия в энергиях. Эта тонкая структура свидетельствует о действии квантового числа l. Экспериментальным доказательством существования квантового числа m является эффект Зеемана, а именно расщепление спектральных линий в магнитном поле. Все p-орбитали с данным n вырождены, но в присутствии магнитного поля появляются небольшие отличия в энергиях, соответствующие различным квантованным ориентациям вектора углового момента орбитали относительно поля.
4.6 ВИД АТОМНЫХ ОРБИТАЛЕЙ
Важные для химика-экспериментатора сведения можно получить, рассмотрев вид различных орбиталей являющихся приемлемыми решениями уравнения Шрёдингера. Напомним, что, согласно требованиям принципа неопределенности, мы можем судить о нахождении электрона на различных орбиталях (s, p, d, f) в определенных положениях только в терминах вероятностей y2. Рассмотрим подробно s-орбитали. Уравнения для Is-, 2s- и 3s-орбиталей и аналогичные выражения для других s-орбиталей показывают, что амплитуда y не зависит от углов q и j>, которые не появляются в формулах для этих орбиталей. Поскольку ydt не зависит от углов, s-орбитали должны обладать сферической симметрией относительно ядра. котором изображена. Такая поверхность дает представление о виде s-орбитали и является графиком зависимости r от q и j в сферических координатах
S - орбитали
р- орбитали
d - орбитали
. р-Орбитали являются трехмерными поверхностями, которые можно представить себе, рассматривая поверхности, возникающие при вращенииих двумерных изображений на 180° вокруг осей. d-Орбитали также являются трехмерными поверхностями; орбиталь dx-y располагается вдоль осей х и у, орбиталь dxy—между осями х и у, dyz—между у и z, dxz—между х и z, a dz — вдоль оси z.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.235 (0.01 с.) |


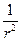 )(
)(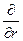 )(r2
)(r2  ) + (
) + ( )(
)( )(sinq
)(sinq  ) +
) + )(
)( ) +
) +  )y = 0
)y = 0 ,
,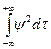 = 1
= 1