
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Химический потенциал. ЛетучестьСодержание книги
Поиск на нашем сайте
Все, что сказано было об термодинамических потенциалах, относилось к закрытой системе, в которой масса сохраняется постоянной. При изучении растворов и гетерогенных систем, состоящих из двух или более веществ, необходимо рассматривать открытые системы, где состав и масса могут быть непостоянными вследствие химических реакций и других процессов. Энергия Гиббса в этом случае является функцией не только Т и Р, но и количеств n1,n2,...ni молей компонентов. G = f(T,P,n1, n2,....ni) dG = ( ni - постоянное число молей всех компонентов nj - постоянное число молей всех компонентов, кроме одного, изменение которого рассматривается ( Химический потенциал, частная производная энергии Гиббса по массе i-того компонента при постоянных Р и Т и массах остальных компонентов. dGP,T = m1 dn1 + m2 dn2 +....+ mI dni dGP,T = S mI dni Для равновесия S mi dni= 0 Любые равновесные свойства газов можно выразить через химический потенциал При Т = const dG = VdP dm = VdP m = V = dm = m = m0+ RT lnP m0 - стандартный химический потенциал m2 - m1 = RT ln Химический потенциал реального газа можно вычислить двумя способами. Первый способ состоит в том, что для решения уравнения объем газа выражают через давление, используя одно из уравнений реального газа. (P + Другой способ предложил Льюис. При этом используются те же выражения что и для вычисления химического потенциала идеального газа, но вместо давления в них подставляют переменную - летучесть или фугитивность - f. dm = RTd lnf m = m* + RT lnf m2 - m1 = Dm = RT ln Отношение летучести к давлению реального газа называется коэффициентом летучести g = f = g P Коэффициенты летучести вычисляют на основе принципа соответственных состояний. Он заключается в том, что при одинаковых приведенных параметрах все газы обладают приблизительно одинаковыми свойствами. Приведенным параметром называется отношение этого параметра к его критическому значению. p = t = В соответствие с этим принципом при одинаковых приведенных параметрах газы обладают приблизительно одинаковыми коэффициентами летучести. Коэффициент летучести по этому способу определяют при помощи графика lgg - lgp при разных значениях приведенной температуры.
1.19 ХИМИЧЕСКОЕ РАВНОВЕСИЕ.ЗАКОН ДЕЙСТВУЮЩИХ МАСС
1799 - Бертолле 1864 - Гульдберг и Вааге При постоянной температуре отношение произведений равновесных концентраций продуктов реакции в степени их стехиометрических коэффициентов к произведению равновесных концентраций исходных веществ в степени их стехиометрических коэффициентов есть величина постоянная. Кинетический вывод n1 A1 + n2 A2 = n3 A3 + n4 A4 v1 =k1 При равновесии v1 = v2 k1 K = термодинамичеcкий вывод Smidni = 0 mi = mi0 + RT lnPi n3m3 + n4m4 - n1m1 - n2m2 = (n3m30 + n4m40 - n1m10 - n2m20) + RT (n3lnP3 + n4lnP4 - n1 lnP1 - n2 lnP2) = 0 ln Kp = Константа равновесия может выражаться через различные величины через давление - Kp, через концентрации - Kc, через мольные доли - KN, через активности - Ka. PV = nRT P = n/V RT P = CRT Kp= Kp = Kc (RT)Dn Pi = P Ni Kp = Kp = KN PDn
УРАВНЕНИЕ ИЗОТЕРМЫ РЕАКЦИИ ΔG = Σμidni = ν3 μ3 + ν4 μ4 – ν1 μ1 – ν2 μ2 ΔG = RT (ν3 μ03 + ν4 μ04 – ν1 μ01 – ν2 μ02) + RT (ν3 lnP13 + + ν4 lnP14 – ν1 lnP11 – ν2 lnP12) ΔG = RT (ν3 lnP13 + ν4 lnP14 – ν1 lnP11 – ν2 lnP12) - RTlnKp ΔG = RT (ln ΔG = RT (lnK1p - lnKp) если Рi = 1 атм ΔG0 = - RT lnKp Kp = e-ΔG0/RT уравнение нормального химического сродства Уравнение изотермы позволяет получить возможность определить направление процесса 1. lnK1 p < lnKp ΔG < 0 реакция идет в прямом направлении 2. lnK1p > lnKp ΔG > 0 реакция идет в обратном направлении 3. lnK1p = lnKp ΔG = 0 равновесие
1.21 ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ТЕМПЕРАТУРЫ
ΔG = Δ H + T( ΔG = RT(lnK1p - lnKp) = ΔH + T(RlnK1p - RlnKp - RT ΔH = RT2
ΔH > 0 T↑ Kp↑ ΔH < 0 T↑ Kp↓ N2 + 3H2 = 2NH3 - экзотермическая реакция Следовательно, синтез аммиака следует проводить при низких температурах. Интегрирование уравнения дает ln(
1.21 ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ДАВЛЕНИЯ
Kp = KN PΔn KN = Kp P-Δn lnKN = lnKp - ΔnlnP
PΔV = ΔnRT
ΔV > 0 P↑ KN ↓ ΔV < 0 P↑ KN ↑
1.22 ПРИНЦИП ПОДВИЖНОГО РАВНОВЕСИЯ (ПРИНЦИП ЛЕ-ШАТЕЛЬЕ)
Анализируя характер влияния температуры на константу равновесия и степень превращения, можно заметить,что увеличение температуры всегда смещает равновесие в эндотермическом направлении. Это значит, например, что если реакция экзотермическая, то при dT>0 равновесие смещается влево, т.е. в направлении, когда выделение теплоты уменьшается и, наоборот, если реакция эндотермическая, то увеличение температуры смещает равновесие вправо. По принципу Ле-Шателье - Брауна - любая физико-химическая система, находящаяся в состоянии равновесия, стремится удержать состояние равновесия и на любое влияние извне отвечает процессом, который стремится парализовать это влияние, противостоять изменениями смещает систему в новое состояние равновесия.
ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА
Сопоставление тепловых эффектов и изменения энергии Гиббса в реакциях, происходящих в конденсированных системах при различных температурах, показывает, что в области низких температур при приближении к абсолютному нулю значения тепловых эффектов и изменения энергии Гиббса сближаются. Тепловая теорема является постулатом, утверждающим, что это сближение продолжается и при дальнейшем понижении температуры, причем при абсолютном нуле и вблизи него кривые соприкасаются и общая для них касательная параллельна оси температур.
Математически ΔG = ΔH lim│ Из тепловой теоремы вытекает ряд следствий ( lim[ΔS]T→0 = 0 [ΔS]T=0 = 0 т.е. вблизи абсолютного нуля все реакции, совершающиеся в конденсированных системах,не сопровождаются изменением энтропии. Второе следствие получим, применяя условие ( lim[ΔC]T→0 = 0 [ΔC]T=0 = 0 т.е. вблизи абсолютного нуля изменение теплоемкости твердых реагирующих веществ бесконечно мало отличается от нуля. Можно показать, что при очень низких температурах не только ΔS и ΔС твердых тел стремятся к нулю, но и многие другие свойства тел (объем, давление насыщенного пара и др.) изменяются с температурой так, что их производные по температуре стремятся к нулю. Этим объясняется принцип недостижимости абсолютного нуля (называемый также третьим законом термодинамики),согласно которому никакие процессы не могут снизить температуру до абсолютного нуля.
1.24 РАСЧЕТ ХИМИЧЕСКОГО РАВНОВЕСИЯ С ПОМОЩЬЮ СТАНДАРТНЫХТЕРМОДИНАМИЧЕСКИХ ВЕЛИЧИН
В настоящее время известны стандартные теплоты образования и энтропии более 7500 простых веществ и соединений. С помощью этих табличных данных можно вычислить термодинамические параметры многих десятков тысяч реакций, в том числе предполагаемых и не изученных экспериментально. В методе расчета, основанном на использовании стандартных термодинамических величин, используются два исходных уравнения ΔG0T = ΔH0T – TΔS0T lnK0P = - ΔG0T /RT Если нет никаких предварительных сведений о положении равновесия при интересующей нас температуре, расчет ΔG и Кр полезно производить в две стадии. В первой стадии вычисляют изменение энергии Гиббса при Т = 298К и для стандартных условий. Для расчета ΔН0298 и ΔS0298 используют уравнения ΔH0298 = (nΔH0298,f)кон - (nΔH0298f)нач ΔS0298 = (nS0298)кон - (nS0298)нач По величине и знаку Не следует думать, что реакция неосуществима вообще, если по расчету получится сравнительно небольшая величина ΔG0298.Реакция невозможна только в стандартных условиях, но, вероятно, может протекать при иных температурах и давлении, при непрерывном удалении продуктов реакции из зоны реакции. Точный расчет (вторая стадия) покажет - при каком сочетании указанных факторов величина энергии Гиббса станет отрицательной и как она должна быть изменена дальше, чтобы выход продуктов реакции сделался достаточно большим. В качестве ориентировочного критерия, определяющего целесообразность второго этапа расчетов, рекомендуется величина ΔG0298 = 418кдж/моль На второй стадии расчета переходят от значения ΔG0298 к значению ΔG0т при других температурах. Для этого необходимо вычислить ΔH0т и ΔS0т при заданной Т. ΔH0т = ΔН0298 + ΔS0т = ΔS0298 + ΔG0т = ΔH0298 – TΔS0298 +
Если пренебречь влиянием изменения теплоемкости, т. е. ΔСр = 0,то решение уравнения будет грубо приближенным ΔG0т = ΔH0298 – TΔS0298 Данное приближение (первое приближение Улиха) необходимо для быстрой оценки возможности протекания реакции при интересующей температуре. При выполнении точного расчета подставляется зависимость ΔСр = f(T) ΔCр = Δа + ΔвТ + ΔсТ2 + Δс1 Т-2 Проведя интегрирование, получим ΔG0 т = ΔH0298 – TΔS 0298 - T{Δa(ln + + DG0T = DH0298 - T×DS0298 – T(DaM0 + DbM1 + DcM2 + Dc1M-2. Коэффициенты М0,М1,М2, М-2 рассчитаны для разных температур, их значения можно найти в справочнике. Этот метод расчета называется методом Темкина – Шварцмана.
ФАЗОВЫЕ РАВНОВЕСИЯ ОБЩИЕ ПОНЯТИЯ ФАЗА (Ф) - совокупность всех однородных частей системы, имеющих одинаковый химический состав, одинаковые физические свойства и физические границы, отделяющие их от других частей системы. СОСТАВЛЯЮЩИЕ ВЕЩЕСТВА СИСТЕМЫ - это индивидуальные химические вещества, которые могут быть выделены из системы и могут существовать вне ее самостоятельно. КОМПОНЕНТЫ СИСТЕМЫ (К) - индивидуальные вещества, наименьшее число которых необходимо и достаточно для образования всех возможных фаз системы, находящейся в равновесном состоянии. Следовательно, компоненты - это независимые составляющие вещества системы. Число компонентов равняется числу составляющих веществ минус число уравнений, связывающих эти концентрации при равновесии. ТЕРМОДИНАМИЧЕСКАЯ СТЕПЕНЬ СВОБОДЫ (С) - показывает число независимых термодинамических параметров системы, находящейся в равновесии, изменение которых в определенных пределах не вызывает исчезновения одних и появления других фаз. ФАЗОВОЕ РАВНОВЕСИЕ - равновесие в гетерогенной системе, состоящей из двух или большего числа фаз, и характеризующейся равенством скоростей перехода вещества из одной фазы в другую для любой пары фаз.
УСЛОВИЯ ФАЗОВОГО РАВНОВЕСИЯ
Условие самопроизвольного перехода компонента из фазы a mi(a) > mi(a) Поскольку mi = mi 0 + RT ln P i Pi (a) = Pi (b) fi (a) = fi (b)
ПРАВИЛО ФАЗ ГИББСА
Рассмотрим равновесную термодинамическую систему, состоящую из Ф фаз, каждая из которых содержит К компонентов. Примем в качестве параметров, определяющих состояние системы, температуру, давление и концентрацию компонентов и оценим общее число этих параметров. Число параметров одинаковых во всех фазах равно 2 - (Т и Р).Если концентрации компонентов выражены в мольных долях, то для характеристики состава одной фазы достаточно знать (К - 1) концентраций. Для характеристики состава всех фаз необходимо знать Ф(К - 1) концентраций. Тогда общее число параметров, определяющих состояние системы, будет равно Ф(К - 1) + 2. Число уравнений, связывающих концентрации компонентов, можно определить из равенства химических потенциалов каждого компонента во всех фазах. m11 = m12 = m13 =.........= m1ф m21 = m22 = m23 =.........= m2ф ............................................ К mк1 = mк2 = mк3 =........= mкф ________________________________ Ф - 1 Число уравнений, связывающих концентрации всех компонентов равно К(Ф - 1). Число независимых параметров системы, т. е. число термодинамических степеней свободы равно разности между общим числом параметров, определяющих состояние системы и числом уравнений, связывающих эти параметры. С = Ф(К - 1) + 2 - К(Ф - 1) С = К + 2 – Ф Правило фаз - в равновесной термодинамической системе, на которую из внешних факторов оказывают влияние только температура и давление, число термодинамических степеней свободы равно числу компонентов минус число фаз плюс два.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 524; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.012 с.) |

 )Р,п dT + (
)Р,п dT + ( )т,ni dP + (
)т,ni dP + ( )p,т,nj dn1+ +.(
)p,т,nj dn1+ +.( )p,т,njdni
)p,т,njdni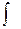 VdP + C
VdP + C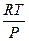
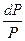 = RT
= RT 
 ) (v - b) = RT - уравнение Ван-дер Ваальса
) (v - b) = RT - уравнение Ван-дер Ваальса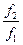
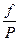
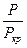

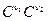 v2 = k2
v2 = k2 

 = -
= -  (n3m30 + n4m40- n1m10 - n2m20) = lnKp
(n3m30 + n4m40- n1m10 - n2m20) = lnKp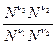 P(n3+n4-n1-n2)
P(n3+n4-n1-n2) ) – lnKp - уравнение изотермы
) – lnKp - уравнение изотермы )p
)p )
) - уравнение изобары
- уравнение изобары =
=  - уравнение изохоры
- уравнение изохоры ) = -
) = - 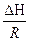 (
( -
- 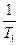 )
)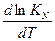 = -
= - 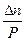
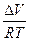

 │T→0 = lim│
│T→0 = lim│  │T→0 = 0
│T→0 = 0 ΔG0298 судят о возможности получения желаемых веществ из взятых исходных в стандартных условиях.
ΔG0298 судят о возможности получения желаемых веществ из взятых исходных в стандартных условиях. ΔСрdT
ΔСрdT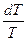
 +
+  - 1) +
- 1) + (T - 2×298 +
(T - 2×298 +  ) +
) +  (Т2 - 3×2982 +
(Т2 - 3×2982 +  ) - Dс1(-
) - Dс1(- 
 +
+  )}.
)}.


