Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ионная связь. Энергия кристаллической решеткиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
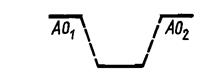
Чисто ионная связь отвечает электростатической модели. Проверкой электростатической модели служит возможность расчета энергии кристаллической решетки. Рассмотрим взаимодействие 2-х точечных зарядов с помощью кривой потенциальной энергии.
Е = Епр + Еотт = │ Для однозарядных атомов Z1 =Z2 =1 En = - Чтобы получить энергию всего кристалла следует это выражение помножить на общее число ионов, кроме того учесть еще слагаемые возникающие от сил притяжения и отталкивания более высокого порядка в результате действия второго, третьего и других соседних ионов в кристалле. Первый фактор легко учесть, если взять кристалл, содержащий по 1 грамм-иону каждого типа. Второй фактор зависит от вида кристаллической решетки и называется константой Маделунга - A. А-NaCl = 1,74756; А-CsCl = 1,76267
Ep =
Экспериментальная проверка электростатической модели может быть сделана или непосредственным изучением равновесия в парообразной фазе MX = M+ +X- или косвенным методом, используя круговой процесс, известный под названием цикла Борна-Габерна.
Насколько успешно можно пользоваться электростатической моделью говорят результаты Соединение Ер выч Ер цикл Ер практ. NaCl 184,3 183,9 181,3 NaBr 174,6 175,5 176 NaJ 167,9 164,8 166 Для расчета энергии кристаллической решетки применяется также уравнение Капустинского E = 1073 где n - число ионов, на которые распадается молекула данного соединения r1,r2 - радиусы ионов
КОВАЛЕНТНАЯ СВЯЗЬ
5.3 МЕТОД МОЛЕКУЛЯРНЫХ ОРБИТАЛЕЙ Метод МО есть распространенный на молекулы метод атомных орбиталей. Предполагается, что электроны в молекуле находятся на орбиталях, охватывающих все ядра в молекуле. Для построения волновой функции основного состояния молекулы распределяют все ее электроны по МО с наименьшей энергией по вариационному методу, учитывая ограничения, налагаемые принципом Паули, согласно которому на одной орбитали не может находиться больше двух электронов. Чаще всего в методе МО применяют приближение ЛКАО для построения МО. Вблизи ядра электроны находятся в поле потенциала, создаваемого в основном этим ядром. Поле, обусловленное другими ядрами, в этой области сравнительно мало. Поэтому, вблизи ядра МО должна быть близка к АО соответствующего атома. Учитывая это, предполагают, что разумное приближение к МО во всех точках пространства можно получить, беря линейную комбинацию атомных орбиталей, относящихся ко всем атомам в молекуле.
y = åciji y -МО j -АО сi- коэффициенты Если в это разложение включить достаточно большое число АО, то, вычисляя коэффициенты на основе вариационного принципа, можно получить хорошее приближение к истинной МО. Рассмотрим сущность вариационного метода. Уравнение Шредингера Нy=Еy Е- полная энергия молекулы Умножив обе части на ydt и проинтегрировав получим E = Если волновая функция является одним из решений волнового уравнения, то расчет по этой формуле дает значение дозволенного уровня энергии электрона Е, dt - элемент объема пространства. Если представить искомую волновую функцию в виде y1 = c1j1 + c2j2 + ¼+cnjn то выражение может быть записано
где e меняется в зависимости от выбора y и называется энергетической функцией. В вариационном методе исходят из того, что чем меньше энергетическая функция,тем она ближе к действительному значению энергии основного состояния, а выбранная функция к истинной. Очевидно, что при подстановке уравнение величина энергетической функции будет зависеть от коэффициентов с1,.с2, cn. Согласно вариационному методу эти коэффициенты нужно выбирать так, чтобы значения энергетической функции были минимальными. Это удобно делать, рассматривая коэффициенты как переменные величины. Тогда условия минимума выразятся системой уравнений
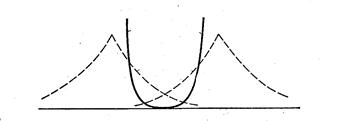
Решение системы уравнений позволяет найти значения с1,с2,сn, при которых энергетическая функция минимальна. В качестве примера рассмотрим простейшую молекулярную частицу - молекулярный ион водорода Н2+. Согласно метода ЛКАО молекулярную орбиталь можно представить в виде y = с1 jа + с2 jв где а и в - обозначения ядер Поскольку атомы неразличимы, то плотность вероятности нахождения электрона около каждого из ядер должна быть одной и той же. Это выполняется в случае с12 = с22 с1 = с2 yg = Сg (ja+ jb) с1 = -с2 yu = Сu (ja - jb) yg - симметричная волновая функция yu - антисимметричная волновая функция Симметричная функция отражает увеличение плотности электронного облака в области перекрывания между двумя атомами по сравнению с плотностью облаков отдельных атомов.
Увеличение плотности отрицательно заряженного электронного облака между положительными ядрами приводит к тому, что ядра как бы стягиваются этим облаком и возникает химическая связь.
Система электрон в поле двух протонов находится в энергетически более выгодном состоянии Е,чем исходная система электрон в поле одного протона
Eg Поэтому yg называется связывающей молекулярной орбиталью. Антисимметричной волновой функции отвечает уменьшение плотности электронного облака между атомами. При этом полoжительно заряженные атомы отталкиваются и система становится неустойчивой.
Молекулярной орбитали отвечает энергия большая, чем энергия атома водорода
Eu
Eg Орбиталь yu,соответствующая повышению энергии, называется разрыхляющей МО.
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.241.124 (0.007 с.) |



 │r=r0 = 0
│r=r0 = 0 (1-
(1- 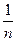 )
)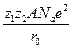 (1-
(1- 
 10-4
10-4  ån
ån
 e =
e = 
 = 0
= 0 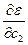 = 0 ………
= 0 ………  = 0
= 0