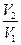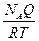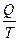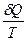Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимость теплового эффекта oт температуры.Содержание книги
Поиск на нашем сайте
УРАВНЕНИЯ КИРХГОФФА Рассмотрим зависимость теплоты процесса при постоянных давлении и объеме от температуры. Возьмем производную по температуре от теплоты процесса: ( ( отсюда получаем
Эти уравнения называются уравнениями Кирхгоффа, из них следует, что температурный коэффициент процесса равен изменению теплоемкости в результате протекания этого процесса. Для химической реакции aA + bB = dD + eE изменение теплоемкости DСp = dCPD + eCPE – aCPA - bCPB DCP= SnпродСр прод - SnисхСР исх из уравнения следует, что если изменение теплоемкости процесса положительно, то с ростом температуры тепловой эффект увеличивается и наоборот при DСр >0 при DCp < 0 при DСр = 0 тепловой эффект процесса не зависит от Т. Интегрируя уравнение, получаем DH2 = DH1 + Для аналитического вычисления теплового эффекта нужно знать зависимость DСр от температуры. Если DСр = а = const DH2 = DH1 + a(T2 – T1) Более точные результаты получаются, если использовать в расчетах зависимость теплоемкости от температуры DСр = Dа + DвТ +DсТ2 + Dс` /T2 После интегрирования получим DH2 = DH1 + Da(T2 – T1) + - Dc1(1/T2 - 1/T1) Чаще всего Т1 = 298 К
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Все протекающие в природе процессы следуют первому началу термодинамики, но не всякий процесс, не противоречащий первому началу, осуществим на практике. Из первого начала вытекает лишь, что энергия изолированной системы постоянна, определить же направление процесса, происходящее в системе, нельзя. Второй закон термодинамики, так же как и первый, не может быть найден из каких-либо общих положений, и устанавливается на основании опыта. Он дает возможность разделить все допускаемые первым законом процессы на самопроизвольно и несамопроизвольно протекающие в данных условиях. Второй закон устанавливает, какой процесс может протекать и в каком направлении в данной системе при рассматриваемых условиях без сообщения энергии извне, т.е. самопроизвольно, каков предел его протекания и какое количество работы может быть получено при этом. Было предложено несколько формулировок второго закона термодинамики. Карно(1824) - в тепловых машинах теплота, полученная от теплоисточника, не может быть полностью переведена в механическую работу, часть ее должна быть передана третьему телу - холодильнику. Клаузиус(1850) - теплота не может переходить от холодного тела к горячему сама собой. Кельвин(1854) - невозможно превратить в работу теплоту какого-либо тела, не производя никакого другого действия,кроме охлаждения этого тела. Оствальд - осуществление вечного двигателя второго рода невозможно. Под вечным двигателем второго рода подразумевается такая периодически действующая тепловая машина, которая способна была бы полностью превращать теплоту в работу, т.е. без передачи части ее холодильнику.
ЭНТРОПИЯ
Односторонность протекания процессов в природе является следствием молекулярной природы вещества. Рассмотрим поведение молекул в закрытом сосуде, разделенном перегородкой. Вероятность нахождения молекул в одной части сосуда будет мала, а вероятность равномерного распределения всех молекул по объему - велика. Математически для одной молекулы вероятность равна В термодинамике используют понятие термодинамической вероятности, равное числу способов, каким может быть осуществлено данное состояние. Обозначается W. Она является функцией состояния и максимальна при равновесии. Сложная система из 2-х систем с вероятностью W1 и W2 будет иметь вероятность W12 = W1 W2.Такое свойство, когда целое является произведением составляющих называется мультипликативностью. В термодинамике надо иметь такую функцию вероятности, котoрая была бы связана с тепловыми характеристиками, обладала свойствами аддитивности и принимала экстремальные значения при равновесии. Для этого введена функция - энтропия. S = f(W1 W2) = f(W1) + f(W2) S = k lnW S12 = k ln(W1 W2) = k ln W1 + ln W2 = S1 + S2 Рассмотрим расширение газа от объема V1 до V2 и определим изменение энтропии. DS = S2 – S1 = k ln
DS = k NA ln Q = RT ln DS = k k Na = R k - константа Больцмана DS = dS = Из первого закона dQ = dU + dW
dS =
dU = TdS – dW - объединенное выражение первого и второго закона термодинамики.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.21.237 (0.008 с.) |

 )P = D(
)P = D(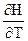 )P = DCP
)P = DCP )V = D(
)V = D(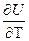 ))V = DCv
))V = DCv = DCp
= DCp = DCv
= DCv DCpdT
DCpdT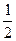 Db(T22 – T12) +
Db(T22 – T12) +  Dc(T23- T13) -
Dc(T23- T13) -