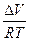Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исторический очерк развития физической химииСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Стерлитамакский филиал
В.С. БЫКОВСКИЙ
ФИЗИЧЕСКАЯ ХИМИЯ
(КОНСПЕКТ ЛЕКЦИЙ) Часть первая
Учебное пособие
Стерлитамак 2002
УДК 541.1(075) Физическая химия.(конспект лекций).Часть первая / В. С. Быковский; Уфим. гос. нефт. техн. университет, 2002. – ISBN
В пособие включены разделы - химическая термодинамика, химическое равновесие, растворы, строение вещества. Учебное пособие предназначено для студентов специальности 250100 – «Химическая технология органических веществ» и может быть полезно студентам специальности 320700 – «Охрана окружающей среды и рациональное использование природных ресурсов».
Рецензент: Садыков Н. Б., доцент кафедры ОХТ Стерлитамакского филиала УГНТУ., канд.хим.наук
© Уфимский государственный нефтяной технический университет, 2002
ВВЕДЕНИЕ
Физическая химия - наука о закономерностях химических процессов и химических явлений. Она объясняет эти явления на основе фундаментальных положений физики и стремится к количественному описанию химических процессов. Объектами ее являются любые системы, в которых могут протекать химические превращения. Физическая химия изучает происходящие в этих системах изменения, сопровождающиеся переходом химической формы движения в различные физические формы движения - тепловую, электрическую и др. Таким образом, физическая химия изучает химические процессы не сами по себе, а в неразрывной связи сопровождающими их физическими явлениями. К главным задачам физической химии можно отнести изучение и объяснение основных закономерностей, определяющих направление химических процессов, скорость их протекания, условия получения максимального выхода необходимых продуктов. Центральной задачей является установление связи между строением вещества и его реакционной способностью. Современная физическая химия служит теоретическим основанием химической технологии. Физическая химия включает следующие основные разделы. СТРОЕНИЕ ВЕЩЕСТВА - учение о строении атомов и молекул, природе химической связи, молекулярной спектроскопии. ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА - учение о взаимосвязи между теплотой химической реакции и других видов энергий, позволяет определять направление реакции, рассчитать условия равновесия. РАСТВОРЫ - учение о природе растворов и их важнейших свойствах. ЭЛЕКТРОХИМИЯ - учение о взаимосвязи между химической и электрической энергией, свойства растворов электролитов, электропроводность растворов, электродные процессы и электрохимическую коррозию. ХИМИЧЕСКАЯ КИНЕТИКА И КАТАЛИЗ - учение о скорости и механизме химических реакций. ФОТОХИМИЯ - учение о влиянии световой энергии на химические процессы. КОЛЛОИДНАЯ ХИМИЯ - учение о дисперсных системах
ИСТОРИЧЕСКИЙ ОЧЕРК РАЗВИТИЯ ФИЗИЧЕСКОЙ ХИМИИ
Физическая химия как наука возникла в середине 18 века. Основоположник М.В. Ломоносов (1711 - 1765).Им была составлена программа по физической химии и в 1752-1754 гг. прочитан "Курс истинной физической химии". Он же дал первое определение предмета - "Физическая химия - наука, объясняющая на основании положений и опытов физических причину того, что происходит через химические операции в сложных телах". В течение последующего столетия проводились исследования, на основе которых было сделано много важных открытий. Лавуазье и Лаплас во Франции(1779-1785) изучали теплоемкости веществ и тепловые эффекты реакций. В начале19 века Деви в Англии и Тенаром во Франции были открыты каталитические реакции. Гальвани и Вольта в Италии создали в 1799 г. гальванический элемент. В.В. Петров в России в 1802 г. открыл явление электрической дуги, а Т. Гротгус заложил основы электролиза. М. Фарадей в Англии сформулировал количественные законы электролиза Д. Дальтон (Англия,1801-1803),Л. Гей-Люссак (Франция,1802),А. Авогадро (Италия,1811) открыли законы газового состояния. Труды Карно Майера, Джоуля, Гесса, Клаузиуса, Гиббса, Вант-Гоффа, Нернста в области термодинамики, Максвелла, Больцмана и Гиббса в области молекулярно-кинетической теории и статистической физики составили фундамент и физической химии. К. Гульдберг и П. Вааге в Норвегии (1864-1867), Д. Гиббс в США(1873-1878) развили термодинамическое учение о химическом равновесии, а Ле Шателье во Франции (1884) открыл общий принцип смещения равновесия при изменении внешних условий. С. Аррениус в Швеции (1883-1887) развил теорию электролитической диссоциации. Д.И. Менделеев открыл существование критической температуры,вывел общее уравнение состояния газов и разработал химическую теорию растворов. Д.П. Коновалов, его ученик, является основоположником теории растворов. Впервые после Ломоносова преподавание курса физической химии снова ввел Н.Н. Бекетов, который с 1860 г. начал читать в Харьковском университете курс "Отношение физических и химических явлений между собой" и с 1865 г. - курс, названный им "Физическая химия". Первый учебник по физической химии был создан в России в 1876 г. Н.Н. Любавиным. В 20 веке революция в физике, связанная с трудами Планка, Резерфорда, Бора, Эйнштейна, Шредингера в области квантовой механики атомов и молекул привела к рассмотрению химических процессов на атомно-молекулярном уровне, созданию теории химической связи трудами Льюиса, Лондона, Гейтлера, Полинга, Слэтера. Из отечественных ученых, сделавших большой вклад в развитие физической химии, можно отметить Н.Н. Семенова (химическая кинетика),А.А. Баландина (катализ),Я.К. Сыркина (строение вещества),А.Н. Фрумкина (электрохимия) и многих других. Как и другие науки, физическая химия и отдельные ее разделы возникали или начинали развиваться особенно успешно в те периоды, когда та или иная практическая потребность вызывала необходимость быстрого роста какой-либо отрасли промышленности, а для этого развития требовалась прочная теоретическая основа.
ХИМИЧЕСКАЯ ТЕРМОДИНАМИКА
ПРЕДМЕТ И ЗАДАЧИ ТЕРМОДИНАМИКИ
Термодинамика возникла в конце первой половины 19 века. В тот период цель термодинамики сводилась к установлению взаимосвязи между теплотой и работой и разработке теории паровой машины. В дальнейшем цели термодинамики расширяются и основные ее положения используются в различных областях, в том числе и химии. Термодинамика базируется на трех законах, из которых все остальные положения данной науки можно получить путем логических рассуждений. Первый закон термодинамики связан с законом сохранения энергии и позволяет рассчитывать тепловые балансы процессов. Второй закон термодинамики - закон о возможности протекания самопроизвольных процессов. Третий закон термодинамики - закон об абсолютном значении энтропии. Та часть термодинамики, которая имеет дело с применением этих законов к химическим процессам и фазовым переходам называется химической термодинамикой. Химическая термодинамика разрабатывает наиболее рациональные методы расчета тепловых эффектов химических процессов, раскрывает закономерности при равновесии, определяет благоприятные условия для осуществления химического процесса.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ
СИСТЕМА - тело или группа тел, мысленно выделенная из окружающей среды. ОТКРЫТАЯ СИСТЕМА - система, которая может обмениваться с окружающей средой энергией и веществом. ЗАКРЫТАЯ СИСТЕМА - отсутствует обмен веществом с окружающей средой, но она может обмениваться энергией с ней. ИЗОЛИРОВАННАЯ СИСТЕМА - система, объем которой остается постоянным и которая не обменивается энергией и веществом с окружающей средой. Система может быть гомогенной или гетерогенной. Совокупность всех физических и химических свойств системы называется состоянием системы. Свойства, которые могут быть выражены через функции температуры, давления и концентрации веществ называются термодинамическими. Для полного описания системы достаточно знать некоторое наименьшее число термодинамических свойств, которые рассматривают как внутренние параметры системы (параметры состояния системы). Обычно в качестве параметров состояния системы выбирают такие ее свойства, которые наиболее легко определить экспериментальным путем, например давление (Р),объем (V),температура (Т) и концентрация (Сi)компонентов. Параметры состояния системы связаны между собой соотношением, которое называется уравнением состояния. В общем виде f(P,V,T) = 0 PV = n RT ТЕРМОДИНАМИЧЕСКИЙ ПРОЦЕСС - изменение во времени хотя бы одного из термодинамических свойств. САМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ - процессы, не требующие затраты энергии извне. НЕСАМОПРОИЗВОЛЬНЫЕ ПРОЦЕССЫ -процессы, требующие затраты энергии. РАВНОВЕСНОЕ СОСТОЯНИЕ - состояние системы, которое сохраняется неизменным во времени. ПОСТУЛАТ - Протекание самопроизвольного процесса в конечном счете приводит систему в равновесное состояние. ВНУТРЕННЯЯ ЭНЕРГИЯ - совокупность всех видов энергии частиц в системе. Обозначается U. Является функцией состояния, т.е. ее изменение не зависит от того как идет процесс, а будет определяться только исходным и конечным состояниями системы. РАБОТА ПРОЦЕССА - форма передачи энергии от изучаемой системы к окружаюшей среде или от окружающей среды к системе путем преодоления сил, действующих на систему со стороны окружающих тел или в противоположном направлении. Обозначается W(A). Работа, совершаемая системой, принимается положительной, а работа окружающей среды отрицательной. Полная работа (W) рассматривается как сумма работ изменения объема системы и всех других видов работ, связанных с преодолением сил, действующих на систему, называемых полезной работой (Wп). Работа определяется соотношением W = Если действующая сила вызвана внешним давлением (F = PS), где S - площадь, к которой приложено давление, то работа преодоления внешнего давления W = Полная работа W = ТЕПЛОТА ПРОЦЕССА (Q) - форма передачи энергии от изучаемой системы к окружающей среде путем микрофизических процессов (столкновений молекул).Теплота считается положительной, когда она подводится к системе.
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Он является по существу законом сохранения энергии, представленным в форме, удобной для термодинамического анализа. Закон сохранения энергии - энергия не возникает из ничего и не исчезает бесследно, она может лишь в различных формах переходить от одних тел к другим, но общее ее количество в изолированной системе не изменится ни при каких условиях. В термодинамике изменение внутренней энергии системы выражается через количество теплоты и работ, которыми система обменивается с окружающей средой. С учетом правила знаков первый закон термодинамики математически выражается DU = Q - W = Q - Для бесконечно малого изменения
dU =δQ - δW =δQ - PdV - δWn
Формулировки первого закона 1.Изменение внутренней энергии термодинамической системы равно разности между количеством теплоты, подведенной к системе и количеством работы, совершенной системой. 2.Вечный двигатель первого рода невозможен или нельзя совершать работу без затраты энергии. 3.Внутренняя энергия изолированной системы постоянна (dU = 0, U = const)
И СГОРАНИЯ
1.По энергии разрыва связей DHf = S(nieI)исх + nQCвозг - S(nieI)кон где e - энергия разрыва связей,QCвозг - теплота возгонки углерода 2.Эмпирическая формула расчета теплоты сгорания органического соединения в газообразном состоянии DHc298 = - (204,2 n + 44,4 m + Σx) кдж/моль, где n - число атомов кислорода, необходимое для полного сгорания вещества m - число молей образующейся воды Σх - поправка (термическая характериcтика), которая находится по справочнику для различных гомологических рядов 3.Метод тепловых поправок Расчет строится на основе значений DН0f298 для веществ, лежащих в основе соответствующего гомологического ряда. В эти основные величины вводят поправки на увеличение углеродной цепи, замещение простых связей сложными и т.д. Порядок расчета 1.Выбирают основное вещество, из которого минимальным числом замещений можно получить структурную формулу соединения. Находят DНf 298 основного вещества. 2.Последовательным введением в основное вещество групп –СН3 строят углеродный скелет рассматриваемого соединения, при этом на каждую группу - СН3 вносят поправки в основную величину DНf 298. 3.После построения углеродного скелета соединения замещают простые связи сложными и вводят соответствующие поправки. 4.Замещают группировки –СН3 другими группами и вводят соответствующие поправки.
1.6 ТЕПЛОЕМКОСТЬ. СВЯЗЬ ТЕПЛОЕМКОСТИ С ТЕРМОДИНАМИЧЕСКИМИ ФУНКЦИЯМИ
Теплоемкостью называют количество теплоты, необходимое для нагревания единицы массы вещества на 1 К. Различают удельную и молярную теплоемкости. Также различают истинную и среднюю теплоемкости. Средней молярной теплоемкостью называют отношение количества теплоты, подведенного к одному молю вещества, к разности температур (Т2 – Т1). С = Истинной молярной теплоемкостью называют отношение бесконечно малого количества теплоты, которое нужно подвести к одному молю вещества, к бесконечно малому приращению температуры, которое при этом наблюдается . C = Q = С = CV = DU = DU = CV (T2 – T1) CP= DH = DH = CP(T2 –T1) В расчетах Ср определяют по опытным данным для Сv и наоборот. Для этого нужно знать разность теплоемкостей (Cp – Cv). Cp - Cv = Теплоемкость вещества лишь в сравнительно узком интервале температур можно считать независимой от температуры. Вообще говоря, теплоемкость есть сложная функция от температуры и может быть рассчитана лишь квантовомеханически. Практически зависимость теплоемкости выражается с помощью ряда, коэффициенты которого определяются опытным путем. Ср = а + вТ + с Т2 СV = а + вТ + с`Т-2
УРАВНЕНИЯ КИРХГОФФА Рассмотрим зависимость теплоты процесса при постоянных давлении и объеме от температуры. Возьмем производную по температуре от теплоты процесса: ( ( отсюда получаем
Эти уравнения называются уравнениями Кирхгоффа, из них следует, что температурный коэффициент процесса равен изменению теплоемкости в результате протекания этого процесса. Для химической реакции aA + bB = dD + eE изменение теплоемкости DСp = dCPD + eCPE – aCPA - bCPB DCP= SnпродСр прод - SnисхСР исх из уравнения следует, что если изменение теплоемкости процесса положительно, то с ростом температуры тепловой эффект увеличивается и наоборот при DСр >0 при DCp < 0 при DСр = 0 тепловой эффект процесса не зависит от Т. Интегрируя уравнение, получаем DH2 = DH1 + Для аналитического вычисления теплового эффекта нужно знать зависимость DСр от температуры. Если DСр = а = const DH2 = DH1 + a(T2 – T1) Более точные результаты получаются, если использовать в расчетах зависимость теплоемкости от температуры DСр = Dа + DвТ +DсТ2 + Dс` /T2 После интегрирования получим DH2 = DH1 + Da(T2 – T1) + - Dc1(1/T2 - 1/T1) Чаще всего Т1 = 298 К
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Все протекающие в природе процессы следуют первому началу термодинамики, но не всякий процесс, не противоречащий первому началу, осуществим на практике. Из первого начала вытекает лишь, что энергия изолированной системы постоянна, определить же направление процесса, происходящее в системе, нельзя. Второй закон термодинамики, так же как и первый, не может быть найден из каких-либо общих положений, и устанавливается на основании опыта. Он дает возможность разделить все допускаемые первым законом процессы на самопроизвольно и несамопроизвольно протекающие в данных условиях. Второй закон устанавливает, какой процесс может протекать и в каком направлении в данной системе при рассматриваемых условиях без сообщения энергии извне, т.е. самопроизвольно, каков предел его протекания и какое количество работы может быть получено при этом. Было предложено несколько формулировок второго закона термодинамики. Карно(1824) - в тепловых машинах теплота, полученная от теплоисточника, не может быть полностью переведена в механическую работу, часть ее должна быть передана третьему телу - холодильнику. Клаузиус(1850) - теплота не может переходить от холодного тела к горячему сама собой. Кельвин(1854) - невозможно превратить в работу теплоту какого-либо тела, не производя никакого другого действия,кроме охлаждения этого тела. Оствальд - осуществление вечного двигателя второго рода невозможно. Под вечным двигателем второго рода подразумевается такая периодически действующая тепловая машина, которая способна была бы полностью превращать теплоту в работу, т.е. без передачи части ее холодильнику.
ЭНТРОПИЯ
Односторонность протекания процессов в природе является следствием молекулярной природы вещества. Рассмотрим поведение молекул в закрытом сосуде, разделенном перегородкой. Вероятность нахождения молекул в одной части сосуда будет мала, а вероятность равномерного распределения всех молекул по объему - велика. Математически для одной молекулы вероятность равна В термодинамике используют понятие термодинамической вероятности, равное числу способов, каким может быть осуществлено данное состояние. Обозначается W. Она является функцией состояния и максимальна при равновесии. Сложная система из 2-х систем с вероятностью W1 и W2 будет иметь вероятность W12 = W1 W2.Такое свойство, когда целое является произведением составляющих называется мультипликативностью. В термодинамике надо иметь такую функцию вероятности, котoрая была бы связана с тепловыми характеристиками, обладала свойствами аддитивности и принимала экстремальные значения при равновесии. Для этого введена функция - энтропия. S = f(W1 W2) = f(W1) + f(W2) S = k lnW S12 = k ln(W1 W2) = k ln W1 + ln W2 = S1 + S2 Рассмотрим расширение газа от объема V1 до V2 и определим изменение энтропии. DS = S2 – S1 = k ln
DS = k NA ln Q = RT ln DS = k k Na = R k - константа Больцмана DS = dS = Из первого закона dQ = dU + dW
dS =
dU = TdS – dW - объединенное выражение первого и второго закона термодинамики.
НЕОБРАТИМЫХ ПРОЦЕССОВ
Представим, что система переходит из начального состояния в конечное двумя путями - обратимо и необратимо. Qобр = DU + Wобр Qнеобр = DU + Wнеобр т.к. величина ΔU определяется только начальным и конечным состоянием системы и поэтому одинаковы в обоих процессах. Wнеобр < Wобр следовательно Qнеобр < Qобр Для обратимого процесса dQобр = TdS dS = DS = S2 – S1 =
dS = 0 DS = 0 Для необратимого процесса dQнеобр < TdS dS > DS >
dS > 0 DS > 0 TdS ³dU + dW TdS ³ dU + PdV При протекании в изолированной системе обратимого процесса энтропия системы остается постоянной DS = 0 Если в ней будет протекать неравновесный процесс, то энтропия будет возрастать DS > 0 В общем случае в изолированной системе DS ³ 0 Исследуя энтропию, очевидно можно предсказывать направление процесса. Если в изолированной системе для какого-либо процесса энтропия возрастает, то процесс возможен (может протекать самопроизвольно),если энтропия согласно расчета должна убывать, то процесс невозможен. При постоянстве энтропии процесс равновесен. Причем при равновесии энтропия достигает максимально возможного значения.
1.11 ИЗМЕНЕНИЕ ЭНТРОПИИ В РАЗЛИЧНЫХ ПРОЦЕССАХ
Для расчета изменения энтропии при равновесных процессах используется соотношение dS = 1.Изменение энтропии при фазовых превращениях Фазовые превращения происходит при постоянной температуре
DS = S2 – S1 = где DНФП - теплота фазового перехода, Т - температура фазового перехода. Энтропия при фазовых превращениях изменяется скачком. 2.Изменение энтропии при изотермическом расширении (сжатии) моля газа DS = dQ = RT dln DS = R ln 3.Изменение энтропии при нагревании системы dS = DS = DS = CР ln CР = a + bT + c T2 DS = aln 4.Изменение энтропии идеального газа dQ = dU + dW dQ = nCV dT + PdV
= nCV dlnT + nRdlnV = nCP dlnT - nRdlnP DS = nCV ln а) изотермический процесс DS = nRln б) изохорический процесс DS = nCV ln в) изобарный процесс DS = nCP ln
ПОСТУЛАТ ПЛАНКА.ВЫЧИСЛЕНИЕ АБСОЛЮТНОЙ ЭНТРОПИИ
В 1912 г. М. Планк высказал не связанное ни с первым ни со вторым законом термодинамики и экспериментально недоказуемое утверждение (постулат),что при абсолютном нуле энтропия чистого кристаллического вещества равна нулю. В отличие от первого и второго законов термодинамики из постулата Планка нельзя вывести новые фундаментальные понятия. Однако предсказание lim S = 0 настолько хорошо согласуется с опытом и настолько важно, что постулат Планка называют третьим законом термодинамики. Формулировка - любое вещество имеет определенную положительную энтропию, но при абсолютном нуле энтропия может стать равной нулю и она равна нулю для чистых правильно образованных кристаллических веществ. Третий закон оправдан теоретическими соображениями. Согласно уравнения Больцмана S = k lnW S = 0,когда W = 1.Значению W = 1 отвечает единственно возможное макросостояние - идеально правильно построенный кристалл, в кристаллической решетке которого атомы занимают узлы в строгом соответствии с геометрическими законами. В реальных кристаллах вследствие их образования и охлаждения в неравновесных условиях имеются различные дефекты структуры. Поэтому энтропия реальных кристаллов при 0 К должна быть больше нуля. Фактически энтропия реальных кристаллов мало отличается от нуля и этой разницей пренебрегают без ущерба для термодинамических расчетов. Третий закон используется при вычислениях абсолютных энтропий простых и сложных веществ. Абсолютной энтропией называется энтропия, отсчитанная относительно нуля К. SТ = SТ – SО = + С целью сравнения и табулирования энтропии веществ относят к стандартному состоянию, температуре 298 К и обозначают S0298. Стандартные энтропии удобны для расчета изменения энтропии в химических реакциях по формуле DS = S (ni S0298)кон - S(ni S0298)исх DSТ = DS298 +
1.13 ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
ПОТЕНЦИАЛ) Работа равновесного процесса максимальна - Wмаx dWmax = TdS - dU = -d(U - TS) U - TS = A(F) – Энергия Гельмгольца (изохорно-изотермический потенциал) Wmax = -DA dA = dU - TdS - SdT dW £ TdS - dU dU £ TdS - PdV dA £ TdS - PdV - TdS - SdT £ -SdT - PdV (¶A/¶T)V £ -S (¶A/¶T)T £ - P Энтропия служит мерой убыли энергии Гельмгольца с увеличением температуры, а давление - мерой ее убыли с увеличением объема системы. (¶A)V,T £ 0 Энергия Гельмгольца системы, находящейся при постоянных V и Т не изменяется при равновесных процессах и убывает при неравновесных процессах. Направление неравновесного процесса определяется убылью энергии Гельмгольца.
1.15 ЭНЕРГИЯ ГИББСА (ИЗОБАРНО-ИЗОТЕРМИЧЕСКИЙ ПОТЕНЦИАЛ)
dU = dQ - PdV - dWn dWn = - dU + TdS - PdV dWn = - (dU - TdS + PdV) = - d(U - TS + PV) = -dG U - TS + PV = G - Энергия Гиббса Wn = - DG G = U - TS + PV = H - TS = A + PV dG £ dA + PdV + VdP £ -SdT - PdV + PdV + VdP dG £ - SdT + VdP (¶G/¶T)P £ -S (¶G/¶P)T £ V (¶G)P,T £ 0 Энергия Гиббса при постоянных Р и Т уменьшается при неравновесных процессах и остается постоянной при равновесных процессах. Равновесное состояние при данных Р и Т соответствует минимуму энергии Гиббса. DG < 0 процесс возможен DG > 0 процесс невозможен DG = 0 процесс равновесен
ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ Для внутренней энергии можно записать dU £ TdS - PdV (¶U)S,V £ 0 -изохорно-изоэнтропный потенциал При всех неравновесных изохорно-изоэнтропных процессах внутренняя энергия убывает, когда величина U достигает минимума система приходит в равновесие. Для энтальпии dH = d(U + PV) £ TdS + VdP (¶H)s,p £ 0 - изобарно-изоэнтропный потенциал dU £ TdS - PdV dH £ TdS + PdV dA £ -SdT - PdV dG £ -SdT + PdV Эти выражения образуют замкнутую группу, в которой две пары переменных T и S (параметры, связанные с теплотой) и Р и V (параметры, связанные с работой) дают все возможные сочетания. Частными производными четырех функций при данном характерном для каждой наборе независимых переменных являются основные параметры состояния системы P,V,S и Т. Отсюда вытекает важное свойство этих функций - через каждую из этих функций и ее производные можно выразить в явной форме любое термодинамическое свойство системы. Каждая функция U = f(S,V) H = f(S,P) A = f(V,T) G = f(P,T) дает таким образом термодинамическую характеристику системы. Поэтому указанные функции называются характеристическими.
УРАВНЕНИЕ ИЗОТЕРМЫ РЕАКЦИИ ΔG = Σμidni = ν3 μ3 + ν4 μ4 – ν1 μ1 – ν2 μ2 ΔG = RT (ν3 μ03 + ν4 μ04 – ν1 μ01 – ν2 μ02) + RT (ν3 lnP13 + + ν4 lnP14 – ν1 lnP11 – ν2 lnP12) ΔG = RT (ν3 lnP13 + ν4 lnP14 – ν1 lnP11 – ν2 lnP12) - RTlnKp ΔG = RT (ln ΔG = RT (lnK1p - lnKp) если Рi = 1 атм ΔG0 = - RT lnKp Kp = e-ΔG0/RT уравнение нормального химического сродства Уравнение изотермы позволяет получить возможность определить направление процесса 1. lnK1 p < lnKp ΔG < 0 реакция идет в прямом направлении 2. lnK1p > lnKp ΔG > 0 реакция идет в обратном направлении 3. lnK1p = lnKp ΔG = 0 равновесие
1.21 ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ТЕМПЕРАТУРЫ
ΔG = Δ H + T( ΔG = RT(lnK1p - lnKp) = ΔH + T(RlnK1p - RlnKp - RT ΔH = RT2
ΔH > 0 T↑ Kp↑ ΔH < 0 T↑ Kp↓ N2 + 3H2 = 2NH3 - экзотермическая реакция Следовательно, синтез аммиака следует проводить при низких температурах. Интегрирование уравнения дает ln(
1.21 ЗАВИСИМОСТЬ КОНСТАНТЫ РАВНОВЕСИЯ ОТ ДАВЛЕНИЯ
Kp = KN PΔn KN = Kp P-Δn lnKN = lnKp - ΔnlnP
PΔV = ΔnRT
ΔV > 0 P↑ KN ↓ ΔV < 0 P↑ KN ↑
1.22 ПРИНЦИП ПОДВИЖНОГО РАВНОВЕСИЯ (ПРИНЦИП ЛЕ-ШАТЕЛЬЕ)
Анализируя характер влияния температуры на константу равновесия и степень превращения, можно заметить,что увеличение температуры всегда смещает равновесие в эндотермическом направлении. Это значит, например, что если реакция экзотермическая, то при dT>0 равновесие смещается влево, т.е. в направлении, когда выделение теплоты уменьшается и, наоборот, если реакция эндотермическая, то увеличение температуры смещает равновесие вправо. По принципу Ле-Шателье - Брауна - любая физико-химическая система, находящаяся в состоянии равновесия, стремится удержать состояние равновесия и на любое влияние извне отвечает процессом, который стремится парализовать это влияние, противостоять изменениями смещает систему в новое состояние равновесия.
ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА
Сопоставление тепловых эффектов и изменения энергии Гиббса в реакциях, происходящих в конденсированных системах при различных температурах, показывает, что в области низких температур при приближении к абсолютному нулю значения тепловых эффектов и изменения энергии Гиббса сближаются. Тепловая теорема является постулатом, утверждающим, что это сближение продолжается и при дальнейшем понижении те
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.93.168 (0.011 с.) |

 F dl
F dl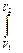 P dV
P dV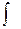 PdV – Wп
PdV – Wп

 =
= 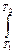 C dT
C dT
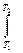 CdT
CdT =
= 
 =
= 
 -
-  )P = D(
)P = D(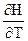 )P = DCP
)P = DCP )V = D(
)V = D(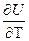 ))V = DCv
))V = DCv = DCp
= DCp = DCv
= DCv DCpdT
DCpdT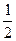 Db(T22 – T12) +
Db(T22 – T12) +  Dc(T23- T13) -
Dc(T23- T13) -

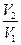
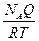
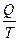
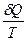

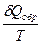
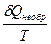
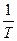
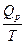 =
=  ,
,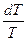
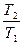
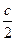 (T22 – T12)
(T22 – T12)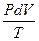 = P/T = nR/V
= P/T = nR/V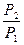
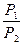
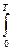 CР ТВ
CР ТВ 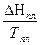 +
+ 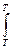 СР Ж
СР Ж 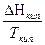 +
+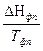
 ) – lnKp - уравнение изотермы
) – lnKp - уравнение изотермы )p
)p )
) - уравнение изобары
- уравнение изобары =
=  - уравнение изохоры
- уравнение изохоры ) = -
) = - 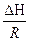 (
( -
- 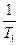 )
)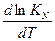 = -
= -