Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Второй закон термодинамики для обратимых иСодержание книги
Поиск на нашем сайте
НЕОБРАТИМЫХ ПРОЦЕССОВ
Представим, что система переходит из начального состояния в конечное двумя путями - обратимо и необратимо. Qобр = DU + Wобр Qнеобр = DU + Wнеобр т.к. величина ΔU определяется только начальным и конечным состоянием системы и поэтому одинаковы в обоих процессах. Wнеобр < Wобр следовательно Qнеобр < Qобр Для обратимого процесса dQобр = TdS dS = DS = S2 – S1 =
dS = 0 DS = 0 Для необратимого процесса dQнеобр < TdS dS > DS >
dS > 0 DS > 0 TdS ³dU + dW TdS ³ dU + PdV При протекании в изолированной системе обратимого процесса энтропия системы остается постоянной DS = 0 Если в ней будет протекать неравновесный процесс, то энтропия будет возрастать DS > 0 В общем случае в изолированной системе DS ³ 0 Исследуя энтропию, очевидно можно предсказывать направление процесса. Если в изолированной системе для какого-либо процесса энтропия возрастает, то процесс возможен (может протекать самопроизвольно),если энтропия согласно расчета должна убывать, то процесс невозможен. При постоянстве энтропии процесс равновесен. Причем при равновесии энтропия достигает максимально возможного значения.
1.11 ИЗМЕНЕНИЕ ЭНТРОПИИ В РАЗЛИЧНЫХ ПРОЦЕССАХ
Для расчета изменения энтропии при равновесных процессах используется соотношение dS = 1.Изменение энтропии при фазовых превращениях Фазовые превращения происходит при постоянной температуре
DS = S2 – S1 = где DНФП - теплота фазового перехода, Т - температура фазового перехода. Энтропия при фазовых превращениях изменяется скачком. 2.Изменение энтропии при изотермическом расширении (сжатии) моля газа DS = dQ = RT dln DS = R ln 3.Изменение энтропии при нагревании системы dS = DS = DS = CР ln CР = a + bT + c T2 DS = aln 4.Изменение энтропии идеального газа dQ = dU + dW dQ = nCV dT + PdV
= nCV dlnT + nRdlnV = nCP dlnT - nRdlnP DS = nCV ln а) изотермический процесс DS = nRln б) изохорический процесс DS = nCV ln в) изобарный процесс DS = nCP ln
ПОСТУЛАТ ПЛАНКА.ВЫЧИСЛЕНИЕ АБСОЛЮТНОЙ ЭНТРОПИИ
В 1912 г. М. Планк высказал не связанное ни с первым ни со вторым законом термодинамики и экспериментально недоказуемое утверждение (постулат),что при абсолютном нуле энтропия чистого кристаллического вещества равна нулю. В отличие от первого и второго законов термодинамики из постулата Планка нельзя вывести новые фундаментальные понятия. Однако предсказание lim S = 0 настолько хорошо согласуется с опытом и настолько важно, что постулат Планка называют третьим законом термодинамики. Формулировка - любое вещество имеет определенную положительную энтропию, но при абсолютном нуле энтропия может стать равной нулю и она равна нулю для чистых правильно образованных кристаллических веществ. Третий закон оправдан теоретическими соображениями. Согласно уравнения Больцмана S = k lnW S = 0,когда W = 1.Значению W = 1 отвечает единственно возможное макросостояние - идеально правильно построенный кристалл, в кристаллической решетке которого атомы занимают узлы в строгом соответствии с геометрическими законами. В реальных кристаллах вследствие их образования и охлаждения в неравновесных условиях имеются различные дефекты структуры. Поэтому энтропия реальных кристаллов при 0 К должна быть больше нуля. Фактически энтропия реальных кристаллов мало отличается от нуля и этой разницей пренебрегают без ущерба для термодинамических расчетов. Третий закон используется при вычислениях абсолютных энтропий простых и сложных веществ. Абсолютной энтропией называется энтропия, отсчитанная относительно нуля К. SТ = SТ – SО = + С целью сравнения и табулирования энтропии веществ относят к стандартному состоянию, температуре 298 К и обозначают S0298. Стандартные энтропии удобны для расчета изменения энтропии в химических реакциях по формуле DS = S (ni S0298)кон - S(ni S0298)исх DSТ = DS298 +
1.13 ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ
ЭНЕРГИЯ ГЕЛЬМГОЛЬЦА (ИЗОХОРНО-ИЗОТЕРМИЧЕСКИЙ ПОТЕНЦИАЛ) Работа равновесного процесса максимальна - Wмаx dWmax = TdS - dU = -d(U - TS) U - TS = A(F) – Энергия Гельмгольца (изохорно-изотермический потенциал) Wmax = -DA dA = dU - TdS - SdT dW £ TdS - dU dU £ TdS - PdV dA £ TdS - PdV - TdS - SdT £ -SdT - PdV (¶A/¶T)V £ -S (¶A/¶T)T £ - P Энтропия служит мерой убыли энергии Гельмгольца с увеличением температуры, а давление - мерой ее убыли с увеличением объема системы. (¶A)V,T £ 0 Энергия Гельмгольца системы, находящейся при постоянных V и Т не изменяется при равновесных процессах и убывает при неравновесных процессах. Направление неравновесного процесса определяется убылью энергии Гельмгольца.
1.15 ЭНЕРГИЯ ГИББСА (ИЗОБАРНО-ИЗОТЕРМИЧЕСКИЙ ПОТЕНЦИАЛ)
dU = dQ - PdV - dWn dWn = - dU + TdS - PdV dWn = - (dU - TdS + PdV) = - d(U - TS + PV) = -dG U - TS + PV = G - Энергия Гиббса Wn = - DG G = U - TS + PV = H - TS = A + PV dG £ dA + PdV + VdP £ -SdT - PdV + PdV + VdP dG £ - SdT + VdP (¶G/¶T)P £ -S (¶G/¶P)T £ V (¶G)P,T £ 0 Энергия Гиббса при постоянных Р и Т уменьшается при неравновесных процессах и остается постоянной при равновесных процессах. Равновесное состояние при данных Р и Т соответствует минимуму энергии Гиббса. DG < 0 процесс возможен DG > 0 процесс невозможен DG = 0 процесс равновесен
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.209.250 (0.01 с.) |

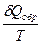
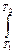
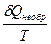
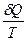
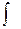 dS =
dS = 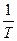
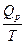 =
=  ,
,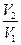
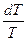
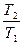
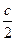 (T22 – T12)
(T22 – T12)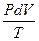 = P/T = nR/V
= P/T = nR/V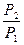
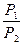
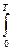 CР ТВ
CР ТВ 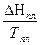 +
+ 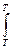 СР Ж
СР Ж 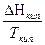 +
+