
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двумя несмешивающимися жидкостямиСодержание книги
Поиск на нашем сайте
Закон распределения - третий компонент, добавленный к системе, состоящей из двух взаимно нерастворимых жидкостей, распределяется между обоими жидкими слоями в определенном, постоянном при данной температуре отношении.
В некоторых системах распределяющееся вещество вследствие диссоциации или ассоциации его молекул обладает неодинаковой средней величиной частиц в различных растворителях. В таких случаях соотношение неприменимо, а закон распределения принимает вид
где n = Для выражения закона распределения в случае концентрированных растворов концентрации следует заменить активностями
где а1 и а2 - активности распределяющегося вещества в первой и второй фазах.
3.13 ЭКСТРАКЦИЯ Закон распределения широко используется для решения задач на экстрагирование вещества из раствора. Экстракцией называется извлечение компонента из раствора с помощью второго растворителя не смешивающегося с первым. Обозначим go - начальное количество экстрагируемого вещества; V1 - объем раствора, в котором находится это вещество; V2 - потребляемый на одно экстрагирование объем растворителя, с помощью которого производится экстрагирование; m -общее число экстрагировании; g1,g2...gm - количество вещества, остающееся в первоначальном растворе после 1,2,..., m-го экстрагировании; К - коэффициент распределения экстрагируемого вещества. Коэффициент распределения экстрагируемого вещества условились обозначать отношением концентрации раствора, из которого экстрагируется распределяющееся вещество, к концентрации раствора, которым производится экстрагирование. Пусть после первого экстрагирования в исходном растворе осталось g1 кг растворенного вещества в объеме Vi, а экстрагируется gэ = go – g1 кг, причем это количество заключается в объеме V2. По закону распределения
откуда
После второго экстрагирования
Если вместо g1 подставить его значение, то получим
Очевидно, что после m экстрагирований в исходном растворе останется gm кг
4. СТРОЕНИЕ АТОМА
4.1 ВОЛНОВЫЕ СВОЙСТВА ЭЛЕКТРОНОВ
Уже в XIX веке было признано, что свет обладает волновыми свойствами, проявляющимися в дифракции от решетки. Однако, согласно данной впоследствии интерпретации фотоэлектрического эффекта, свету были приписаны также и корпускулярные свойства, так что излучение обладает двойственным корпускулярно-волновым характером. Следующие уравнения связывают количественно массу и частоту излучения n с его энергией Е, описывая этот дуализм: E==hv==mc2 Здесь h— постоянная Планка, hv— энергия фотона с массой, эквивалентной т, а с—скорость света. Частота связана с длиной волны l уравнением n= Из уравнений следует l= В 1924 г. де Бройль высказал предположение, что частицы, которые считались корпускулярными, также обладают волновыми свойствами. Уравнение де Бройля связывает длины волн таких частиц с их массой т и скоростью J: l= Подставляя в уравнение значения h, т и J, можно найти длины волн различных частиц, движущихся с определенными скоростями Согласно этим вычислениям, для объектов с массой 1 г или больше, движущихся с обычными скоростями, длины волн настолько малы, что их нельзя измерить. Однако из таблицы легко видеть, что электроны с соответствующими скоростями имеют длины волн, сравнимые с межатомными расстояниями в молекулах и кристаллах. Длины волн, вычисленные для различных частиц
Принцип неопределенности Гейзенберга утверждает, что нельзя одновременно определить точно импульс и положение электрона. Это утверждение можно проиллюстрировать следующим образом. При любом измерении положения электрона излучение, используемое для наблюдения электрона, должно претерпевать изменения. Измеряемая величина—это изменение, происходящее с фотоном при его контакте с электроном. Поэтому нельзя точно обнаружить объект, размеры которого меньше длины волны используемого излучения. Следовательно, чтобы обнаружить такую маленькую частицу, как электрон, необходимо использовать излучение с очень малой длиной волны l и соответственно с очень большой энергией E=hc/l. Однако, поскольку электрон чрезвычайно мал, столкновение с фотоном, обладающим большой энергией, должно изменять его импульс. В результате, чем точнее измеряется положение электрона (при использовании малых длин волн, т. е. фотонов с большой энергией), тем менее точно можно измерить одновременно его импульс (и обратно). Модель атома Бора находится в противоречии с принципом неопределенности, так как она описывает одновременно и положение и импульс электрона. Вместо этого правильная теория может только предсказать вероятность нахождения электрона в определенном положении при данной энергии. После гипотезы де Бройля Шрёдингер интуитивно использовал волновое уравнение в качестве модели для описания поведения электрона в атоме. Эта модель учитывает требования, входящие в принцип неопределенности.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.144.139 (0.006 с.) |

 = К, где C1 - равновесная концентрация распределяющегося вещества в первой фазе; С2 - его равновесная концентрация во второй фазе; К - константа или коэффициент равновесия.
= К, где C1 - равновесная концентрация распределяющегося вещества в первой фазе; С2 - его равновесная концентрация во второй фазе; К - константа или коэффициент равновесия. = К,
= К, (М1 - средний молекулярный вес распределяющегося вещества в первой фазе; М2 - его средний молекулярный вес во второй фазе).
(М1 - средний молекулярный вес распределяющегося вещества в первой фазе; М2 - его средний молекулярный вес во второй фазе). К,
К,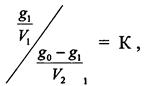

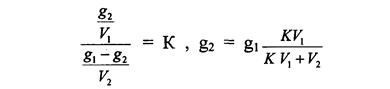



 .
.



