
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение плоскости в отрезках. Неполные уравнения плоскости.
Исследование общего уравнения плоскости
где Если
– плоскость, отсекающая от осейкоординат отрезки величиной а, b и с соответственно, где обозначено
рис.6. Определение. Уравнение
называется неполным уравнением плоскости, если хотя бы один из его коэффициентов А, В, С, D равен нулю. Если
В координатной плоскости Оуz это уравнение есть уравнение прямой, а так как
или или
рис.7.
рис.8.
рис.9. Если
Это уравнение прямой в координатной плоскости Оуz, проходящая через начало координат и в то же время уравнение плоскости, содержащей ось Ох.
рис.10. Если в уравнении (13)
– уравнение координатной плоскости Оху. Если в уравнении (13)
– уравнение координатной плоскости Охz. Ситуации, когда Подведем итог исследованию общего уравнения плоскости
1) Если
где а, b, с – величины отсекаемых плоскостью от координатныхосей отрезков. 2) Если
– плоскость параллельная оси Оz или Оу или Ох соответственно. 3) Если
– соответственно плоскость параллельна координатной плоскости Оуz или Охz или Оху. 4) Если
– плоскость содержит начало координат. 5) Если
– плоскость содержит соответственно ось Ох или ось Оу или ось Оz. 6) Если
п.6. Нормированное уравнение плоскости и прямой на плоскости. Пусть
– векторное уравнение плоскости или прямой на плоскости, где Заметим, что в уравнении (1) длина нормального вектора не играет никакой роли. Выберем в уравнении (1) в качестве нормального вектора
рис.11.
рис.12. Иначе, направление вектора
и разделим обе части уравнения на
где Обозначим
Определение. Уравнение вида
где В случае прямой на координатной плоскости Оху имеем:
Определение. Уравнение вида
где Заметим, что в уравнениях (15) и (16) свободный коэффициент (– р) отрицательный, р численно равно расстоянию от начала координат до плоскости (прямой):
В этом заключается геометрическийсмысл свободного члена р в этих уравнениях. Пример. Записать нормированное уравнение плоскости, если его общее уравнение имеет вид:
и найти расстояние от начала координат до плоскости. Решение. Имеем, Так как свободный коэффициент этого уравнения равен положительному числу 26, то для получения нормированного уравнения плоскости разделим обе части общего уравнения на число, противоположное модулю нормального вектора:
Ответ:
Аналогично приводится к нормальному виду общее уравнение прямой.
28. Уравнение плоскости, проходящей через три заданные точки.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 527; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.60 (0.011 с.) |
 , (7)
, (7)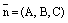 – координаты ее нормального вектора, производится аналогично исследованию общего уравнения прямой на плоскости. Приведем ниже все случаи.
– координаты ее нормального вектора, производится аналогично исследованию общего уравнения прямой на плоскости. Приведем ниже все случаи.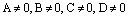 , то уравнение (7) может быть записано в виде уравнения плоскости в отрезках:
, то уравнение (7) может быть записано в виде уравнения плоскости в отрезках: (10)
(10)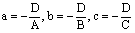 .
.
 , то уравнение (7) имеет вид
, то уравнение (7) имеет вид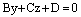 . (11)
. (11)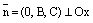 , то данная плоскость параллельна оси Ох. Уравнение (11) может быть записано в виде
, то данная плоскость параллельна оси Ох. Уравнение (11) может быть записано в виде (12)
(12) – уравнение плоскости параллельной координатной плоскости Охz и отсекающей от оси Оу отрезок величины b,
– уравнение плоскости параллельной координатной плоскости Охz и отсекающей от оси Оу отрезок величины b, – уравнение плоскости параллельной координатной плоскости Оху и отсекающей от оси Оz отрезок величины с.
– уравнение плоскости параллельной координатной плоскости Оху и отсекающей от оси Оz отрезок величины с.


 , то уравнение (6) имеет вид
, то уравнение (6) имеет вид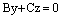 . (13)
. (13)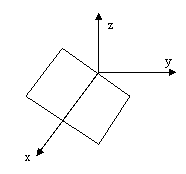
 , то получаем
, то получаем
 , то получаем
, то получаем
 или
или  исследуются аналогично.
исследуются аналогично. , но один из коэффициентов А, В, С равен нулю, то получаем уравнение плоскости в виде
, но один из коэффициентов А, В, С равен нулю, то получаем уравнение плоскости в виде или
или  или
или  или
или 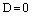 , то уравнение (7) принимает вид
, то уравнение (7) принимает вид
 или
или 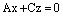 или
или 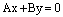
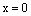 или
или  (1)
(1) – нормальный вектор плоскости (прямой),
– нормальный вектор плоскости (прямой),  – радиус-вектор фиксированной точки плоскости (прямой),
– радиус-вектор фиксированной точки плоскости (прямой),  – радиус-вектор текущей точки плоскости (прямой).
– радиус-вектор текущей точки плоскости (прямой). , а направление нормального вектора выберем такое, чтобы уголмеждувектором
, а направление нормального вектора выберем такое, чтобы уголмеждувектором 

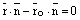
 , если скалярноепроизведение
, если скалярноепроизведение 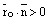 или на
или на  , если
, если  . Получим
. Получим , (14)
, (14) .
. и пусть
и пусть  ,
, 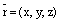 . Так как координатами единичного вектора являются его направляющие косинусы, то
. Так как координатами единичного вектора являются его направляющие косинусы, то 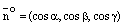 . Подставляя в (14), получаем
. Подставляя в (14), получаем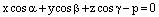 .
. ,
, 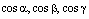 – направляющиекосинусы нормального вектора плоскости, называется нормированным (нормальным) уравнением плоскости.
– направляющиекосинусы нормального вектора плоскости, называется нормированным (нормальным) уравнением плоскости. ,
,  ,
, 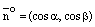 и
и .
.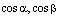 – направляющиекосинусы нормального вектора прямой, называется нормированным (нормальным) уравнением прямой на координатной плоскости Оху.
– направляющиекосинусы нормального вектора прямой, называется нормированным (нормальным) уравнением прямой на координатной плоскости Оху. .
.
 ,
,  .
. .
.


