
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие вектор в геометрии отлично от определяемого в алгебре.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
§ Связанный вектор или направленный отрезок — упорядоченная пара точек евклидова пространства. При этом два направленных отрезка считаются эквивалентными, если они: 1. коллинеарны 2. равны по длине 3. сонаправлены Суммой векторов является вектор - Произведение - Вектор Вектор
15. Разложение вектора по трем некомпланарным векторам. Если дана упорядоченная тройка векторов
16. Проекция вектора на некоторые направление. Теоремы о проекциях. проекцией вектора на ось называется произведение модуля вектора на косинус угла,образованного вектором и положительным направлением оси.
17. Координаты вектора. Направляющие косинусы. . Координа́тыве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
где § Равные векторы в единой системе координат имеют равные координаты § Координаты коллинеарных векторов пропорциональны:
Подразумевается, что координаты вектора b не равны нулю. § Квадрат длины вектора равен сумме квадратов его координат:
§ При умножении вектора на действительное число каждая его координата умножается на это число:
§ При сложении векторов соответствующие координаты векторов складываются:
§ Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
§ Векторное произведение двух векторов можно вычислить с помощью определителя матрицы
где
§ Аналогично, смешанное произведение трех векторов можно найти через определитель
Направляющие косинусы вектора (в пространстве) – это косинусы углов, которые вектор образует с положительными полуосями координат. Направляющие косинусы однозначно задают направление вектора. Если вектор имеет длину 1, то его направляющие косинусы равны его координатам. В общем случае для вектора с координатами (a; b; c) направляющие косинусы равны:
где a, b, g – углы, составляемые вектором с осями x, y, z соответственно.
18. Понятие радиус-вектора данной точки пространства. Расстояние между двумя точками в пространстве. Ра́диус-ве́ктор (обычно обозначается Теорема. Пусть
19. Скалярное произведение векторов и его свойства. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними. Обозначается ab,а* b(или(а, b)).Итак, по определению,
Формуле (6.1) можно придать иной вид. Так как | a| cosg=пр ba, (см. рис.14), a |b| cosg = прab, то получаем:
т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
1. Скалярное произведение обладает переместительным свойством: ab=ba
20 Если векторы
то их скалярное произведение может быть вычислено по формуле
20. Формула для вычисления скалярного произведения векторов.
21. Векторное произведения и его свойства. Векторное произведение и его св-ва Векторным произведением неколлинеарных векторов 1) 2) длина
3)
Обозначение: Свойства: 1) Антикоммутативность 2) Сочетательность (ассоциативностиь) по отношению к скалярному множетилю: 3) Распределительность (дистрибутивность): 4) Если векторы заданы своими координатами:
22. Формула для вычисления векторного произведения векторов.
23. Смешанное произведение и его геометрический смысл Смешанным произведением 3-х векторов Обозначение: Геометрический смысл: Смешанным произведением интерпретируется как число, равное объему параллелограмма, построенного на векторах
24. Формула для вычисления смешанного произведения векторов. Условие компланарности трех векторов. Правая и левая тройка векторов. Если
Условие компланарности 3-х векторов: 3 ненулевых векторов
Правая и левая тройка векторов: 3 некомпланарных векторов
25. Кривые второго порядка
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.159.143 (0.009 с.) |


 , при этом
, при этом  коллинеарен
коллинеарен  .
. некомпланарных векторов, то для любого вектора
некомпланарных векторов, то для любого вектора  существует единственная упорядоченная тройка чисел
существует единственная упорядоченная тройка чисел 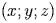 , удовлетворяющая равенству
, удовлетворяющая равенству .
.




 — координаты вектора.
— координаты вектора.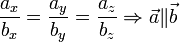









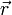 или просто
или просто  ) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
) — вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат. и
и  . Тогда
. Тогда .
.






 и
и  заданы своими координатами:
заданы своими координатами: ,
,  ,
,

 если
если 
 называется вектор
называется вектор  , определяемый условиями:
, определяемый условиями:
 как на сторонах, т.е.:
как на сторонах, т.е.:
 образующие правую тройку
образующие правую тройку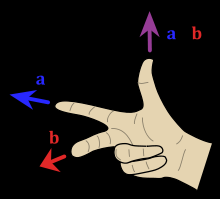 пиздец изображениеце
пиздец изображениеце или
или 



 , если
, если 
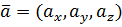 ,
,  то
то или
или 
 где S – площадь параллелограмма
где S – площадь параллелограмма на вектор
на вектор  = (
= (
 , если
, если 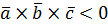 , если
, если  ,
,  ,
,  то
то –ф-ла для вычисления смешанного произведения векторов
–ф-ла для вычисления смешанного произведения векторов
 ко 2-му вектору
ко 2-му вектору  виден совершающимся противчасовой стрелки (по часовой стрелки) ХУЙНЯ КАКАЯТО
виден совершающимся противчасовой стрелки (по часовой стрелки) ХУЙНЯ КАКАЯТО
 в котором по крайней мере один из коэффициентовa11, a 12, a22 отличен от нуля.
в котором по крайней мере один из коэффициентовa11, a 12, a22 отличен от нуля.


