
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расстояние между двумя скрещивающимися прямымиСодержание книги
Поиск на нашем сайте
В координатах
41. Поверхности второго порядка (основные типы) Пове́рхностивторо́гопоря́дка, поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени:
42. Понятие линейного пространства. Примеры л.п. Определение Линейное, или векторное пространство 1. сложения, то есть каждой паре элементов множества 2. умножения на скаляр (то есть элемент поля P), то есть любому элементу При этом на операции накладываются следующие условия: 1. 2. 3. существует такой элемент 4. для любого 5. 6. 7. 8. Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы. Простейшие свойства 1. Векторное пространство является абелевой группой по сложению. 2. Нейтральный элемент 3. 4. Для любого 5. 6. 7.
43. Определение базиса линейного пространства. Теорема о единственности разложения вектора по данному базису.
Базис - любая упорядоченная система Обозначение: Для каждого вектора
Числа
Теорема. (О разложении вектора по базису.) Любой вектор векторного пространства можно разложить по его базису и притом единственным способом. Доказательство. 1) Пусть L произвольная прямая (или ось) и
44. Координаты вектора линейного пространства в данном базисе. Способ определения линейно зависимости векторов линейного пространства. . Пусть e1,e2,…,en – базис пространства V, x,y – произвольные элементы пространства V. При сложении элементов их координаты складываются, при умножении произвольного элемента х на любое число l все координаты этого элемента умножаются на l. [Док-во]: x=a1e1+a2e2+…+anen=i=1ånaiei=(e1,e2,…,en)(a1,a2,…,an). y=b1e1+b2e2+…+bnen=i=1ånbiei=(e1,e2,…,en)(b1,b2,…,bn). 1) x+y= i=1ånaiei+i=1ånbiei=i=1ån(aI+bI)ei=(e1,e2,…,en)(a1+b1,…,an+bn)= (a1+b1)e1+…+(an+bn)en; 2) lx=l* i=1ånaiei= i=1ånlaiei=(e1,e2,…,en)(la1,…,lan)= (la1)e1+…+(lan)en [Лемма]: Пусть e1,e2,…,en базис в пространстве V, f1, f2,…, fn – элементы пространства V. Векторы f1, f2,…, fn линейно зависимы в том и только том случае, когда линейно зависимы столбы их координат. [Док-во]: f1= (e1,e2,…,en)(a1,a2,…,an) l1f1+l2f2+…+lnfn=(e1,e2,…,en)[l1(a11,a12,…,a1n)+…+ln(an1,an2,…,ann)] => вектора f1,f2,…,fnлинейно зависимы в том и только том случае, когда l1(a11,a12,…,a1n)+…+ln(an1,an2,…,ann) = (0,0,…,0) а это значит, что столбцы их координат должны быть линейно зависимыми. Система векторов e 1, e 2,..., e k линейного пространства L называется линейно независимой системой, если равенство С1· e 1+С2 ·e 2+...+Сk · e k = 0 возможно только когда все коэффициенты С1, С2,..., Сk равны нулю. Здесь 0 — нулевой вектор линейного пространства L, С1, С2,..., Сk — числовые коэффициенты. Если система векторов e 1, e 2,..., e k линейного пространства L не является линейно независимой системой, то она называется линейно зависимой системой векторов.
45. Связь между базисами линейного пространства. Матрица перехода (теорема о невырожденной матрицы перехода) Матрица перехода Ма́трицейперехо́да от базиса Обозначается . Так как
Матрица перехода это
46. Преобразование координаты вектора при замене базиса. . Пусть системы векторов e = {e 1,..., e n } и f = {f 1,..., f n } — два базиса n -мерного линейного пространства Ln. Обозначим xe = (x 1, x 2,..., x n) и xf = (x' 1, x' 2,..., x' n) — координаты вектора x ∈ Ln соответственно в базисах e и f. Справедливо следующее xe = Ce→f·xf:
Здесь Ce→f — матрица перехода от базиса e к базису f, это матрица, столбцами которой являются координаты базисных векторов f1,..., f n в базисе e 1,..., e n: f1 = с 11· e2 + с 21 ·e1+... + с n 1 ·e n, f2 = с 12· e1 + с 22 ·e2+... + с n 2 ·e n, ..., f n = с 1 n · e2 +... + с nn ·e n. Формулу преобразования координат вектора при изменении базиса принято записывать в виде xf = (Ce→f)− 1·xe
47. Понятие линейного подпространства. Подпространства решений однородной системы линейных алгебраических уравнений.
Подпространство Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество K линейного пространства L такое, что K само является линейным пространством по отношению к определенным в L действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как Lat (L). Чтобы подмножество было подпространством, необходимо и достаточно, чтобы § § для всякого вектора § для всяких векторов Последние два утверждения эквивалентны следующему: § для всяких векторов В частности, пространство, состоящее из одного элемента {θ}, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными. Свойства подпространств: § Пересечение любого семейства подпространств — снова подпространство; § Сумма конечного семейства подпространств — снова подпространство. Сумма подпространств
В функциональном анализе в бесконечномерных пространствах особо выделяют замкнутые подпространства.
48. Линейные операторы (примеры) Примеры линейных однородных операторов: § оператор дифференцирования: § оператор интегрирования: § оператор умножения на определённую функцию § оператор интегрирования с заданным «весом» § оператор взятия значения функции f в конкретной точке x 0: L { f } = f (x 0)[4]; § оператор умножения вектора на матрицу: b = Ax; § оператор поворота вектора. Примеры линейных неоднородных операторов: § Любое аффинное преобразование; § § § где
49. Матрица линейного оператора. Определение координат образа вектора линейного пространства при действии на него линейного оператора. Матрица линейного оператора — матрица, выражающая линейный оператор в некотором базисе. Для того, чтобы ее получить, необходимо подействовать оператором на векторы базиса и координаты полученных векторов (образов базисных векторов) записать в столбцы матрицы. Матрица оператора аналогична координатам вектора. При этом действие оператора на вектор равносильно умножению матрицы на столбец координат этого вектора в том же базисе.
Выберем базис
где xk — координаты вектора Здесь и далее предполагается суммирование по немым индексам. Пусть
Вектора
где Подставим разложение в предыдущую формулу, получим
Выражение
50. Связь между матрицами линейного операторы в разных базисах.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 609; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.69.226 (0.011 с.) |

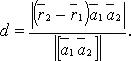
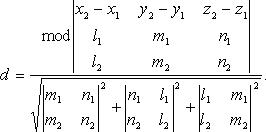
 — эллипсоиды,
— эллипсоиды,  — мнимые эллипсоиды;
— мнимые эллипсоиды; 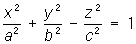 — однополостные гиперболоиды,
— однополостные гиперболоиды, 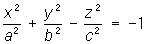 — двуполостные гиперболоиды;
— двуполостные гиперболоиды; 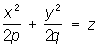 — эллиптические параболоиды,
— эллиптические параболоиды, 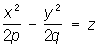 — гиперболические параболоиды;
— гиперболические параболоиды; 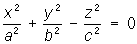 — конусы,
— конусы,  — мнимые конусы;
— мнимые конусы; 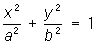 — эллиптические цилиндры,
— эллиптические цилиндры, 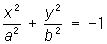 — мнимые эллиптические цилиндры,
— мнимые эллиптические цилиндры, 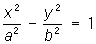 — гиперболические цилиндры,
— гиперболические цилиндры,  — параболические цилиндры.
— параболические цилиндры.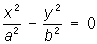 — пары пересекающихся плоскостей,
— пары пересекающихся плоскостей, 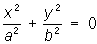 — пары мнимых пересекающихся плоскостей,
— пары мнимых пересекающихся плоскостей, 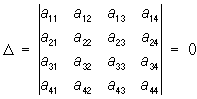 (aij = ajii),
(aij = ajii),  ,
, 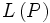 над полем P — это непустое множество L, на котором введены операции
над полем P — это непустое множество L, на котором введены операции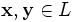 ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый 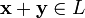 и
и и любому элементу
и любому элементу  ставится в соответствие элемент из
ставится в соответствие элемент из 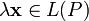 .
.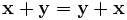 , для любых
, для любых  , для любых
, для любых  (ассоциативность сложения);
(ассоциативность сложения);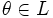 , что
, что 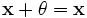 для любого
для любого  , что
, что 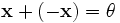 (существование противоположного элемента).
(существование противоположного элемента).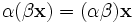 (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр);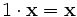 (умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
(умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).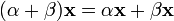 (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров);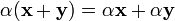 (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов). для любого
для любого 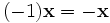 для любого
для любого 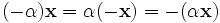 для любых
для любых 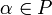 и
и  для любого
для любого 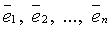 из n линейно независимых векторов пространства
из n линейно независимых векторов пространства 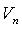 .
.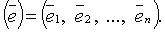
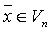 существуют числа
существуют числа 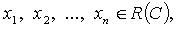 такие что
такие что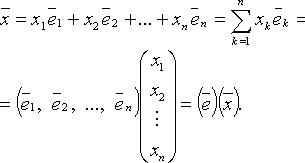
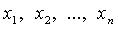 называются координатами вектора
называются координатами вектора 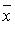 в базисе (
в базисе (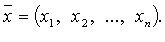
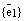 –базис
–базис 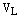 . Возьмем произвольный вектор
. Возьмем произвольный вектор  . Так как оба вектора
. Так как оба вектора  и
и 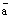 коллинеарные одной и той же прямой L, то
коллинеарные одной и той же прямой L, то 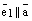 . Воспользуемся теоремой о коллинеарности двух векторов. Так как
. Воспользуемся теоремой о коллинеарности двух векторов. Так как 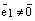 , то найдется (существует) такое число
, то найдется (существует) такое число 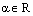 , что
, что 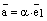 и тем самым мы получили разложение вектора
и тем самым мы получили разложение вектора 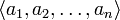 к базису
к базису  является матрица, столбцы которой — координаты разложения векторов
является матрица, столбцы которой — координаты разложения векторов 
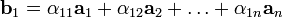 .
.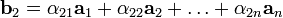 .
.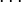 .
. .
.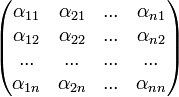

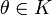 ;
;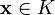 , вектор
, вектор 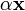 также принадлежал K, при любом
также принадлежал K, при любом 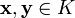 , вектор
, вектор 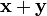 также принадлежал K.
также принадлежал K.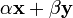 также принадлежал K для любых
также принадлежал K для любых 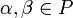 .
.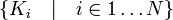 определяется как множество, содержащее всевозможные суммы элементов Ki:
определяется как множество, содержащее всевозможные суммы элементов Ki: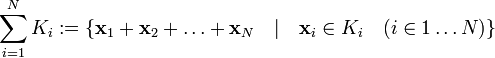 .
.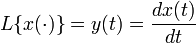 ;
;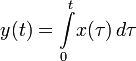 ;
;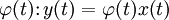 ;
;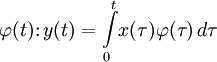
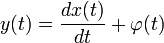 ;
;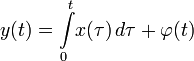 ;
;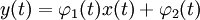 ;
;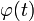 ,
,  ,
, 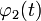 — вполне определённые функции, а x (t) — преобразуемая оператором функция.
— вполне определённые функции, а x (t) — преобразуемая оператором функция. . Пусть
. Пусть  — произвольный вектор. Тогда его можно разложить по этому базису:
— произвольный вектор. Тогда его можно разложить по этому базису: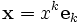 ,
,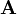 — произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим
— произвольный линейный оператор. Подействуем им на обе стороны предыдущего равенства, получим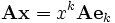 .
.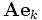 также разложим в выбранном базисе, получим
также разложим в выбранном базисе, получим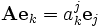 ,
,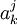 — j -я координата k -го вектора из
— j -я координата k -го вектора из 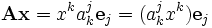 .
. , заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица
, заключённое в скобки, есть ни что иное, как формула умножения матрицы на столбец, и, таким образом, матрица 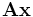 , возникшего от действия оператора
, возникшего от действия оператора  Комментарий: Если в полученной матрице поменять местами пару столбцов или строк, то мы, вообще говоря, получим уже другую матрицу, соответствующую тому же набору базисных элементов
Комментарий: Если в полученной матрице поменять местами пару столбцов или строк, то мы, вообще говоря, получим уже другую матрицу, соответствующую тому же набору базисных элементов 


